What Is The Area Of A Circle? It’s the measurement of the space contained within the circle’s boundary, a fundamental concept in geometry with countless real-world applications. At WHAT.EDU.VN, we aim to provide you with a clear and comprehensive understanding of this essential topic, simplifying complex ideas with easy-to-grasp explanations and examples. Let’s explore circle area calculations, practical applications, and related concepts, unlocking insights into mathematical constants, geometric relationships, and area calculation, empowering you with problem-solving skills.
1. Understanding Circles and Their Parts
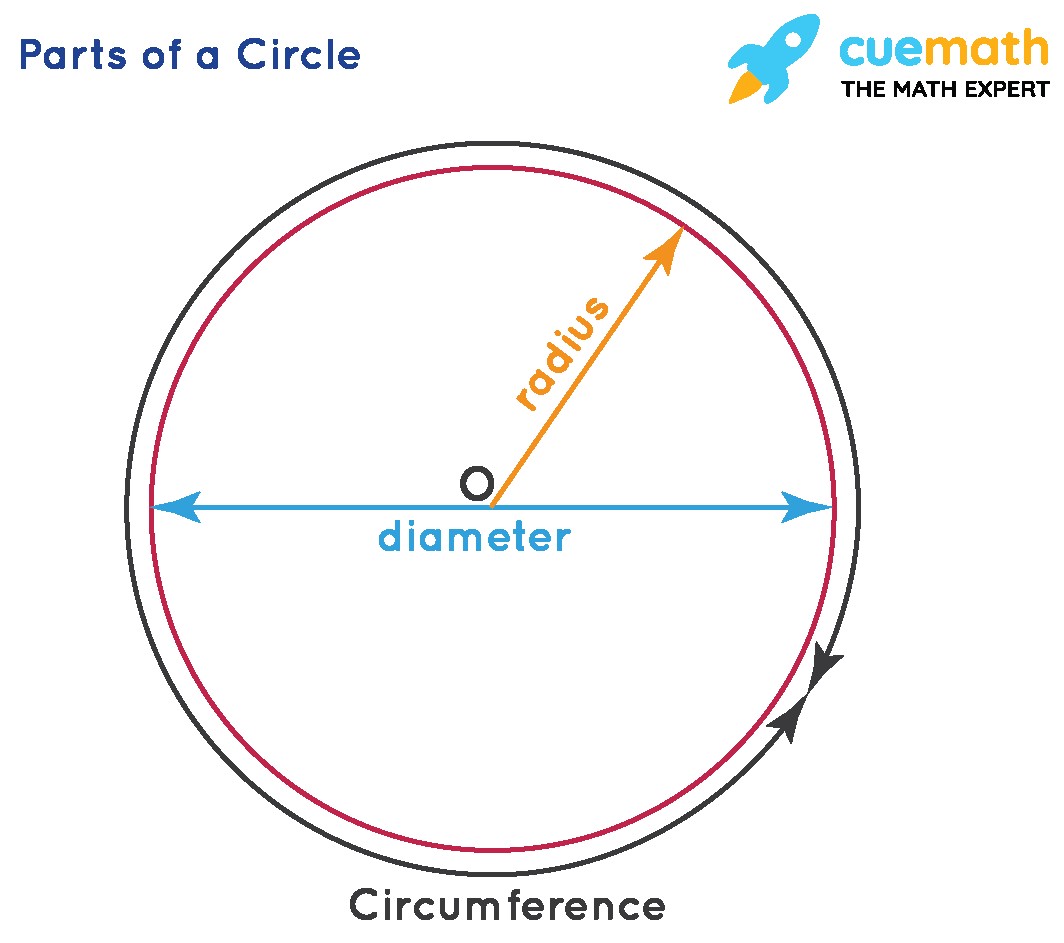
Before diving into calculating the area, it’s crucial to understand the basic components of a circle. These components will be referenced throughout our exploration, so let’s solidify your understanding.
- Center: The central point from which all points on the circle are equidistant.
- Radius (r): The distance from the center to any point on the circle’s edge.
- Diameter (d): A line segment that passes through the center of the circle, connecting two points on opposite sides. The diameter is twice the length of the radius (d = 2r).
- Circumference (C): The distance around the circle’s edge. It’s calculated using the formula C = 2πr, where π (pi) is a mathematical constant approximately equal to 3.14159.
- Chord: A line segment connecting two points on the circle’s edge.
- Arc: A portion of the circle’s circumference.
- Sector: A region bounded by two radii and an arc.
- Segment: A region bounded by a chord and an arc.
2. What Exactly Is the Area of a Circle?
The area of a circle is the measure of the two-dimensional space enclosed within its circumference. Think of it as the amount of paint needed to completely fill the inside of a circle. It’s typically measured in square units, such as square inches (in²), square centimeters (cm²), square feet (ft²), or square meters (m²).
Key Takeaways:
- Area is the space inside the circle.
- It’s a two-dimensional measurement.
- Units are always squared.
3. The Area of a Circle Formula: Unveiled
The formula for calculating the area of a circle is remarkably elegant and straightforward:
A = πr²
Where:
- A represents the area of the circle.
- π (pi) is a mathematical constant approximately equal to 3.14159 (often rounded to 3.14 for simplicity).
- r is the radius of the circle.
This formula tells us that the area of a circle is directly proportional to the square of its radius. If you double the radius, you quadruple the area.
4. Decoding the Formula: A Step-by-Step Guide
Let’s break down how to use the area of a circle formula with a simple example:
Problem: Find the area of a circle with a radius of 5 cm.
Solution:
- Identify the radius: In this case, r = 5 cm.
- Square the radius: r² = 5 cm * 5 cm = 25 cm².
- Multiply by π: A = π 25 cm² ≈ 3.14159 25 cm² ≈ 78.54 cm².
Answer: The area of the circle is approximately 78.54 square centimeters.
5. Alternative Formulas: Area in Terms of Diameter or Circumference
While the standard formula A = πr² is the most common, you can also calculate the area of a circle if you know its diameter or circumference. These alternative formulas are derived from the relationships between radius, diameter, and circumference.
5.1. Area Using Diameter
Since the diameter (d) is twice the radius (r), we have r = d/2. Substituting this into the standard formula, we get:
A = π(d/2)² = πd²/4
Formula: A = πd²/4
5.2. Area Using Circumference
We know that the circumference (C) is related to the radius by the formula C = 2πr. Solving for r, we get r = C/(2π). Substituting this into the standard formula, we get:
A = π[C/(2π)]² = C²/(4π)
Formula: A = C²/(4π)
6. Putting It All Together: Example Problems
Let’s solidify your understanding with a variety of example problems:
Example 1: A circular garden has a diameter of 10 meters. What is its area?
Solution:
- Diameter (d) = 10 meters
- Radius (r) = d/2 = 5 meters
- Area (A) = πr² = π (5 m)² ≈ 3.14159 25 m² ≈ 78.54 m²
Answer: The area of the garden is approximately 78.54 square meters.
Example 2: The circumference of a circular pond is 62.8 feet. What is its area?
Solution:
- Circumference (C) = 62.8 feet
- Area (A) = C²/(4π) = (62.8 ft)² / (4 * π) ≈ 3943.84 ft² / 12.566 ≈ 313.85 ft²
Answer: The area of the pond is approximately 313.85 square feet.
Example 3: A pizza has a radius of 9 inches. What is the area of the pizza?
Solution:
- Radius (r) = 9 inches
- Area (A) = πr² = π (9 in)² ≈ 3.14159 81 in² ≈ 254.47 in²
Answer: The area of the pizza is approximately 254.47 square inches.
7. Unveiling the “Why”: Deriving the Area of a Circle
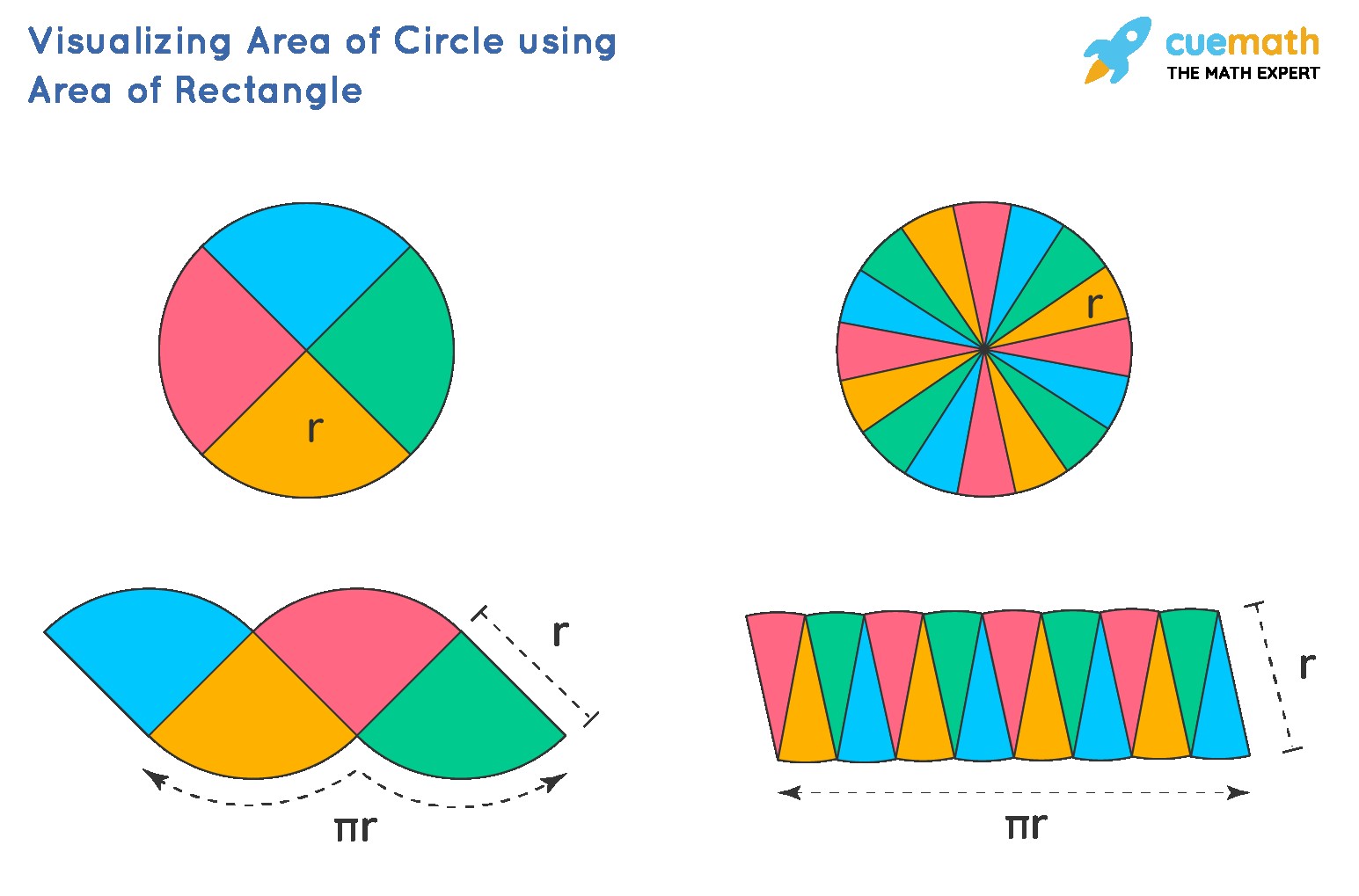
While the formula itself is simple, understanding why it works provides a deeper appreciation for the elegance of mathematics. Here’s a simplified explanation of how the area of a circle formula is derived:
- Divide the Circle: Imagine dividing the circle into many equal sectors, like slices of a pie.
- Rearrange the Sectors: Now, rearrange these sectors to form a shape that resembles a parallelogram. The more sectors you have, the closer the shape gets to being a true parallelogram.
- Parallelogram to Rectangle: As the number of sectors increases infinitely, the parallelogram approaches a rectangle.
- Relate to Circle’s Dimensions:
- The “height” of this rectangle is approximately the radius (r) of the original circle.
- The “base” of this rectangle is approximately half the circumference (C/2 = πr) of the original circle.
- Area of the Rectangle: The area of a rectangle is base height. Therefore, the area of our “rectangle” is approximately (πr) r = πr².
- Conclusion: Since the area of the “rectangle” approximates the area of the circle, we conclude that the area of the circle is A = πr².
8. Area vs. Circumference: Key Differences
It’s important to distinguish between the area and the circumference of a circle:
- Area: The space inside the circle (measured in square units). It answers the question: “How much surface does the circle cover?”
- Circumference: The distance around the circle (measured in linear units). It answers the question: “How long is the circle’s boundary?”
Think of it this way: the area is like the amount of carpet you need to cover a circular floor, while the circumference is like the length of fencing you need to enclose the circular floor.
Table: Area vs. Circumference
| Feature | Area (A) | Circumference (C) |
|---|---|---|
| Definition | Space inside circle | Distance around circle |
| Formula | πr² | 2πr |
| Units | Square units (e.g., cm²) | Linear units (e.g., cm) |
| Measures | Surface covering | Boundary length |
9. Real-World Applications: Where Does This Knowledge Come In Handy?
Calculating the area of a circle isn’t just a theoretical exercise. It has numerous practical applications in various fields:
- Construction: Calculating the amount of material needed for circular structures like swimming pools, patios, or silos.
- Engineering: Designing circular components for machines and equipment, ensuring proper fit and function.
- Architecture: Determining the space occupied by circular features in buildings, such as domes, rotundas, or circular windows.
- Agriculture: Calculating the area of circular fields for irrigation and planting purposes.
- Manufacturing: Determining the amount of material needed to produce circular products like pipes, discs, or lenses.
- Everyday Life: Estimating the size of pizzas, pies, or other circular objects. Figuring out how much fabric you need to make a circular tablecloth.
Examples in Detail:
- Landscaping: A landscaper needs to cover a circular flower bed with mulch. Knowing the diameter of the flower bed, they can calculate the area and determine how much mulch to purchase.
- Cooking: A baker needs to determine the amount of dough required to make a pizza of a specific size. By calculating the area of the pizza, they can accurately measure the ingredients.
- Home Improvement: A homeowner wants to install a circular skylight. They need to calculate the area of the opening to ensure they purchase the correct size skylight.
10. Common Mistakes to Avoid
Calculating the area of a circle is generally straightforward, but here are some common mistakes to watch out for:
- Confusing Radius and Diameter: Always double-check whether you’re given the radius or the diameter. Remember that the radius is half the diameter.
- Forgetting to Square the Radius: The formula is πr², not πr. Make sure you square the radius before multiplying by π.
- Using Incorrect Units: Ensure you’re using consistent units throughout the calculation. If the radius is in centimeters, the area will be in square centimeters.
- Rounding Errors: Be mindful of rounding errors, especially when using π. It’s best to use the full value of π on your calculator or at least keep several decimal places to maintain accuracy.
- Incorrectly Applying the Formula: Ensure you are using the correct formula based on the information provided (radius, diameter, or circumference).
11. Advanced Concepts: Sectors and Segments
Once you’ve mastered calculating the area of a full circle, you can extend your knowledge to calculate the areas of sectors and segments:
11.1. Area of a Sector
A sector is a portion of a circle enclosed by two radii and the arc between them. The area of a sector is a fraction of the total area of the circle, determined by the central angle of the sector.
Formula:
Area of Sector = (θ/360°) * πr²
Where:
- θ is the central angle of the sector in degrees.
- r is the radius of the circle.
Example: A sector has a central angle of 60° in a circle with a radius of 8 cm. What is the area of the sector?
Solution:
Area of Sector = (60°/360°) π (8 cm)² ≈ (1/6) 3.14159 64 cm² ≈ 33.51 cm²
Answer: The area of the sector is approximately 33.51 square centimeters.
11.2. Area of a Segment
A segment is a portion of a circle enclosed by a chord and the arc between the chord’s endpoints. To calculate the area of a segment, you subtract the area of the triangle formed by the chord and the center of the circle from the area of the sector containing the segment.
Formula:
Area of Segment = Area of Sector – Area of Triangle
Where:
- Area of Sector = (θ/360°) * πr²
- Area of Triangle = (1/2) r² sin(θ)
Example: A segment is formed by a chord in a circle with a radius of 10 inches. The central angle of the corresponding sector is 90°. What is the area of the segment?
Solution:
- Area of Sector = (90°/360°) π (10 in)² ≈ (1/4) 3.14159 100 in² ≈ 78.54 in²
- Area of Triangle = (1/2) (10 in)² sin(90°) = (1/2) 100 in² 1 = 50 in²
- Area of Segment = 78.54 in² – 50 in² = 28.54 in²
Answer: The area of the segment is approximately 28.54 square inches.
12. Historical Significance of Pi (π)
Pi (π) is not just a number; it’s a fundamental constant that has fascinated mathematicians for millennia. Its history is rich and intertwined with the development of mathematics itself.
12.1. Ancient Approximations
The quest to understand π dates back to ancient civilizations. Egyptians and Babylonians made early attempts to approximate its value. The Egyptians, around 1650 BC, used an approximation of 3.1605, while the Babylonians, around 1900-1680 BC, used 3.125.
12.2. Archimedes’ Breakthrough
The Greek mathematician Archimedes (c. 287-212 BC) made a significant breakthrough by using polygons inscribed and circumscribed in a circle to approximate π. He calculated the perimeters of these polygons to obtain upper and lower bounds for the circumference of the circle. This method allowed him to determine that π lies between 3 1/7 (approximately 3.1429) and 3 10/71 (approximately 3.1408).
12.3. Further Refinements
Over the centuries, mathematicians from various cultures continued to refine the approximation of π. Chinese mathematician Zu Chongzhi (429-501 AD) calculated π to seven decimal places using a similar method to Archimedes.
12.4. Modern Era
With the advent of calculus and computers, the calculation of π reached new heights. Mathematicians were able to calculate π to an astonishing number of decimal places, revealing its infinite, non-repeating nature.
13. Fun Facts About Circles
Circles are more than just geometric shapes; they are objects of fascination with interesting properties and occurrences in nature.
13.1. Perfect Symmetry
Circles are perfectly symmetrical. They have infinite lines of symmetry passing through the center.
13.2. No Edges
Unlike polygons, circles have no edges or corners, making them unique in the world of shapes.
13.3. Circles in Nature
Circles appear in nature in various forms, from the rings of a tree trunk to the shape of a raindrop falling in a pond.
13.4. The Wheel
The invention of the wheel, based on the circle, revolutionized transportation and technology.
13.5. Celestial Bodies
Many celestial bodies, like the sun and moon, appear circular from our perspective on Earth.
14. Frequently Asked Questions (FAQs)
Let’s address some frequently asked questions about the area of a circle:
Q1: How do I calculate the area of a circle if I only know its radius?
A1: Use the formula A = πr², where ‘r’ is the radius. Square the radius and multiply by π (approximately 3.14159).
Q2: What if I only know the diameter of the circle?
A2: Divide the diameter by 2 to find the radius (r = d/2), then use the formula A = πr². Alternatively, use the formula A = πd²/4.
Q3: Can I calculate the area of a circle if I only know its circumference?
A3: Yes! Use the formula A = C²/(4π), where ‘C’ is the circumference.
Q4: Why is π (pi) used in the area of a circle formula?
A4: Pi (π) is the ratio of a circle’s circumference to its diameter. It’s a fundamental constant that relates the linear dimension of a circle (circumference) to the space it encloses (area).
Q5: What are the units for the area of a circle?
A5: The units for the area of a circle are always square units, such as square inches (in²), square centimeters (cm²), square feet (ft²), or square meters (m²).
Q6: How accurate is the approximation of π as 3.14?
A6: Using 3.14 as an approximation of π is often sufficient for many practical calculations. However, for more precise results, it’s best to use the full value of π on your calculator or a more accurate approximation.
Q7: Does the area of a circle change if I change its orientation?
A7: No, the area of a circle depends only on its radius (or diameter). Rotating or moving the circle in space does not affect its area.
Q8: Is the area of a circle always a positive number?
A8: Yes, the area of a circle is always a positive number. Area represents the amount of space enclosed within the circle, which cannot be negative.
Q9: How does the area of a circle relate to the area of a square with the same side length as the circle’s diameter?
A9: The area of a square with side length equal to the circle’s diameter is d². The area of the circle is πd²/4. Since π/4 is less than 1, the area of the circle is always less than the area of the square.
Q10: Can I use the area of a circle formula to find the area of an oval?
A10: No, the area of a circle formula only applies to perfect circles. Ovals (ellipses) have a different formula for calculating their area, which involves both the major and minor axes of the ellipse.
15. Unlock Your Curiosity: Ask Your Questions on WHAT.EDU.VN
We hope this comprehensive guide has illuminated the concept of the area of a circle. Understanding this fundamental principle opens doors to numerous applications in mathematics, science, and everyday life.
Still have questions? Don’t hesitate! At WHAT.EDU.VN, we’re dedicated to providing you with free and accessible answers to all your queries. Our team of experts is ready to tackle any topic, big or small.
Here’s how we can help:
- Free Question Answering: Ask any question you have, and we’ll provide a clear and concise answer, absolutely free.
- Expert Explanations: Our experts break down complex concepts into easy-to-understand language.
- Fast Responses: Get the answers you need quickly and efficiently.
- Community Support: Connect with other curious learners and share your knowledge.
Ready to get started?
Visit WHAT.EDU.VN today and unleash your curiosity!
Contact Us:
- Address: 888 Question City Plaza, Seattle, WA 98101, United States
- WhatsApp: +1 (206) 555-7890
- Website: WHAT.EDU.VN
Don’t let your questions linger – find the answers you seek at what.edu.vn! We’re here to support your learning journey every step of the way.