Mechanical wave explained. Are you looking for a clearer understanding of mechanical waves and related topics? At WHAT.EDU.VN, we simplify complex concepts. Explore the definitions, characteristics, and formulas that define mechanical waves, and discover how they impact your daily life. Want answers to your questions?
1. Understanding Mechanical Waves: The Basics
A mechanical wave is a type of wave that needs a medium to travel. This medium can be a solid, liquid, or gas. Unlike electromagnetic waves, mechanical waves can’t travel through a vacuum because they need particles to move and transfer energy.
1.1 What Exactly is a Mechanical Wave?
A mechanical wave is a disturbance that moves through a medium, carrying energy from one place to another. Imagine dropping a pebble into a calm pond. The ripples that spread out are mechanical waves. The water itself isn’t moving across the pond, but the energy of the disturbance is.
1.2 The Role of a Medium in Mechanical Wave Propagation
Mechanical waves require a medium—such as air, water, or a solid material—to travel. The particles in the medium vibrate, passing energy from one particle to the next. This is how the wave moves forward.
1.3 Types of Mechanical Waves
There are two primary types of mechanical waves, distinguished by how the particles of the medium move relative to the direction of the wave:
- Transverse Waves: In transverse waves, the particles move perpendicular to the direction of the wave. A classic example is a wave on a string. If you flick one end of a rope, the wave travels along the rope, but each point on the rope moves up and down, not along with the wave.
- Longitudinal Waves: In longitudinal waves, the particles move parallel to the direction of the wave. Sound waves are a perfect example. As a sound wave travels through the air, air molecules compress and expand in the same direction as the wave’s movement.
1.4 Examples of Mechanical Waves in Daily Life
Mechanical waves are all around us. Here are a few examples:
- Sound Waves: The sounds we hear every day are mechanical waves traveling through the air.
- Water Waves: Ripples in a pond or ocean waves are mechanical waves moving through water.
- Seismic Waves: Earthquakes generate seismic waves that travel through the Earth.
- Waves on a String: Musical instruments like guitars and violins use waves on strings to produce sound.
2. Characteristics of Mechanical Waves: Amplitude, Wavelength, Frequency and Wave Speed
To fully understand mechanical waves, it’s important to grasp their key characteristics, including amplitude, wavelength, frequency, and speed.
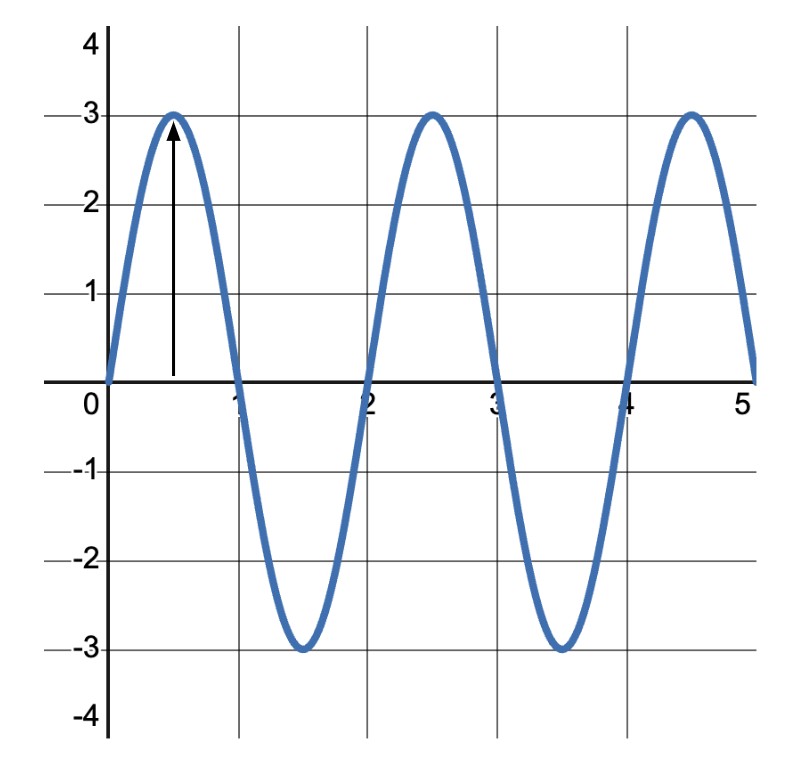
2.1 Amplitude Defined
Amplitude refers to the maximum displacement of a particle in the medium from its resting position. In simpler terms, it’s the height of the wave. For example, in a water wave, the amplitude is the distance from the normal water level to the crest of the wave. A larger amplitude means the wave carries more energy.
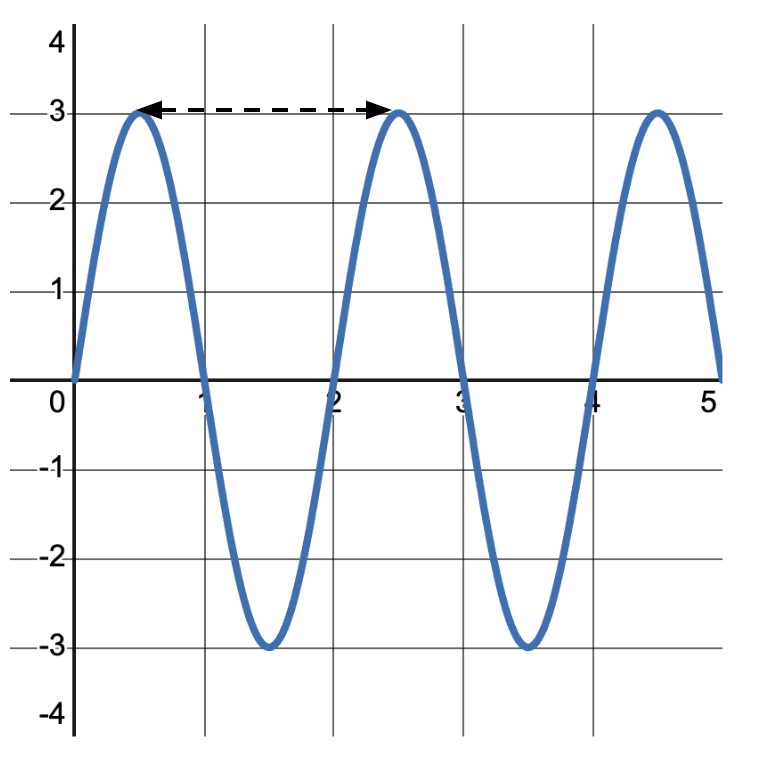
2.2 What is Wavelength?
Wavelength is the distance between two identical points on consecutive waves. It is usually measured from crest to crest or from trough to trough. Wavelength is typically denoted by the Greek letter lambda (λ).
2.3 Frequency Explained
Frequency is the number of complete wave cycles that pass a point in one second. It is measured in Hertz (Hz), where 1 Hz means one cycle per second. For example, if a wave has a frequency of 5 Hz, it means five complete waves pass a point every second.
2.4 Wave Speed Unveiled
Wave speed is the distance a wave travels per unit of time. It depends on the properties of the medium through which the wave is traveling. The relationship between wave speed (v), frequency (f), and wavelength (λ) is given by the wave equation:
v = fλ
This equation tells us that wave speed is the product of the frequency and wavelength.
2.5 The Relationship Between Amplitude and Energy
The amplitude of a mechanical wave is directly related to the amount of energy it carries. A wave with a larger amplitude carries more energy.
For instance, consider sound waves. A louder sound has a higher amplitude, meaning the air molecules are vibrating with greater intensity, carrying more energy to your ears. Similarly, in water waves, larger waves (higher amplitude) have more energy and can cause more significant disturbances.
3. Mechanical Wave Examples in Nature
Mechanical waves play a crucial role in various natural phenomena, shaping our environment and influencing our daily lives in ways we often overlook.
3.1 How Sound Waves Work
Sound waves are perhaps the most familiar example of mechanical waves. When someone speaks, their vocal cords vibrate, creating disturbances in the air. These disturbances travel as longitudinal waves, with air molecules compressing and expanding in the direction of the wave. When these waves reach our ears, they cause our eardrums to vibrate, which our brains interpret as sound.
The speed of sound varies depending on the medium through which it travels. Sound travels faster in solids and liquids than in gases, and its speed also increases with temperature.
3.2 Understanding Water Waves
Water waves are another common example of mechanical waves. These waves can be transverse, longitudinal, or a combination of both, depending on the depth of the water. In deep water, the particles move in circular paths, combining both transverse and longitudinal motion.
Water waves are caused by various factors, including wind, earthquakes, and tides. The size and energy of water waves depend on the strength and duration of the force creating them.
3.3 Seismic Waves and Earthquakes
Seismic waves are mechanical waves that travel through the Earth, usually caused by earthquakes, volcanic eruptions, or explosions. There are two main types of seismic waves:
- P-waves (Primary Waves): These are longitudinal waves that can travel through solids, liquids, and gases. They are the fastest type of seismic wave and are the first to arrive at seismograph stations after an earthquake.
- S-waves (Secondary Waves): These are transverse waves that can only travel through solids. They are slower than P-waves and arrive later at seismograph stations.
By studying the arrival times and characteristics of seismic waves, scientists can learn about the Earth’s interior structure and locate the epicenter of earthquakes.
3.4 The Role of Mechanical Waves in Tsunamis
Tsunamis are a series of powerful water waves caused by large-scale disturbances, such as underwater earthquakes or landslides. These waves have very long wavelengths (often hundreds of kilometers) and can travel at speeds of up to 800 kilometers per hour in the open ocean.
When a tsunami approaches the shore, its speed decreases, and its amplitude increases dramatically, resulting in devastating flooding and destruction. Understanding the behavior of mechanical waves is crucial for predicting and mitigating the impact of tsunamis.
4. Mechanical Wave Applications in Technology
Mechanical waves aren’t just natural phenomena; they’re also harnessed in numerous technological applications that impact our lives daily.
4.1 Ultrasound Technology in Medicine
Ultrasound technology uses high-frequency sound waves to create images of internal body structures. A device called a transducer emits these sound waves, which then bounce off different tissues and organs. The returning echoes are processed to form detailed images, allowing doctors to diagnose and monitor various medical conditions.
Ultrasound is used in:
- Prenatal Care: Monitoring fetal development during pregnancy.
- Diagnostic Imaging: Detecting abnormalities in organs like the liver, kidneys, and heart.
- Therapeutic Applications: Breaking up kidney stones or delivering targeted drug therapies.
4.2 How Sonar Systems Use Mechanical Waves
Sonar (Sound Navigation and Ranging) systems use sound waves to detect and locate objects underwater. These systems emit sound pulses that travel through the water, bounce off objects, and return to the sonar device. By measuring the time it takes for the echo to return, the system can determine the distance and location of the object.
Sonar is used in:
- Navigation: Helping ships and submarines navigate safely.
- Fishing: Locating schools of fish.
- Underwater Mapping: Creating detailed maps of the ocean floor.
4.3 Mechanical Waves in Musical Instruments
Musical instruments rely on mechanical waves to produce sound. Whether it’s the vibration of a string in a guitar, the oscillation of air in a flute, or the striking of a drumhead, mechanical waves are at the heart of music.
- String Instruments: Plucking, bowing, or striking a string creates transverse waves that vibrate at specific frequencies, producing different musical notes.
- Wind Instruments: Blowing air into a wind instrument creates longitudinal waves inside the instrument’s tube. The length and shape of the tube determine the frequencies of the sound waves produced.
- Percussion Instruments: Striking a drumhead or cymbal creates vibrations that produce sound waves. The size, shape, and material of the instrument affect the pitch and tone of the sound.
4.4 Industrial Uses of Mechanical Waves
Mechanical waves have several important applications in industry:
- Ultrasonic Cleaning: High-frequency sound waves are used to clean delicate or hard-to-reach surfaces. The sound waves create tiny bubbles that implode, removing dirt and contaminants.
- Material Testing: Ultrasound can be used to detect flaws and defects in materials without damaging them. This is essential for ensuring the safety and reliability of structures like bridges and aircraft.
- Welding: Ultrasonic welding uses high-frequency sound waves to join materials together. This method is often used to weld plastics and metals.
5. Mathematical Description of Mechanical Waves
Understanding the math behind mechanical waves allows us to predict their behavior and use them effectively in various applications.
5.1 The Wave Equation in Detail
The general wave equation is a second-order partial differential equation that describes the propagation of waves. For a one-dimensional wave, the equation is:
∂²u/∂t² = v² (∂²u/∂x²)
Where:
- u(x, t) is the displacement of the wave at position x and time t.
- v is the wave speed.
This equation applies to various types of waves, including mechanical waves, electromagnetic waves, and even quantum mechanical waves.
5.2 Understanding Superposition
The principle of superposition states that when two or more waves overlap in the same space, the resulting displacement is the sum of the individual displacements of each wave. This principle is essential for understanding phenomena like interference and diffraction.
5.3 Interference Patterns Explained
Interference occurs when two or more waves overlap, resulting in a new wave pattern. There are two main types of interference:
- Constructive Interference: This occurs when the crests of two waves align, resulting in a wave with a larger amplitude.
- Destructive Interference: This occurs when the crest of one wave aligns with the trough of another wave, resulting in a wave with a smaller amplitude or even complete cancellation.
5.4 Diffraction of Mechanical Waves
Diffraction is the bending of waves around obstacles or through openings. The amount of diffraction depends on the wavelength of the wave and the size of the obstacle or opening. When the wavelength is much larger than the obstacle or opening, the wave bends significantly.
6. Transverse vs. Longitudinal Waves: A Detailed Comparison
Mechanical waves come in two primary forms: transverse and longitudinal. Each type has distinct characteristics and behaviors, making them suitable for different applications.
6.1 Particle Motion in Transverse Waves
In transverse waves, the particles of the medium move perpendicular to the direction of the wave. Imagine shaking a rope up and down; the wave travels horizontally along the rope, but each point on the rope moves vertically.
Examples of transverse waves include:
- Waves on a String: As mentioned earlier, these are classic examples of transverse waves.
- Electromagnetic Waves: Light, radio waves, and X-rays are transverse waves, although they don’t require a medium to travel.
- S-waves (Secondary Waves): These seismic waves travel through the Earth’s interior but only through solid materials.
6.2 Particle Motion in Longitudinal Waves
In longitudinal waves, the particles of the medium move parallel to the direction of the wave. Think of a slinky: if you push and pull one end, the compressions and rarefactions travel along the slinky in the same direction as your push and pull.
Examples of longitudinal waves include:
- Sound Waves: These are the most common examples of longitudinal waves.
- P-waves (Primary Waves): These seismic waves travel through the Earth’s interior and can pass through solids, liquids, and gases.
- Ultrasound Waves: Used in medical imaging and industrial applications.
6.3 Key Differences Summarized
Here’s a table summarizing the key differences between transverse and longitudinal waves:
| Feature | Transverse Waves | Longitudinal Waves |
|---|---|---|
| Particle Motion | Perpendicular to wave direction | Parallel to wave direction |
| Wave Type | Crests and troughs | Compressions and rarefactions |
| Medium | Can occur in solids, liquids, and gases | Can occur in solids, liquids, and gases |
| Examples | Waves on a string, light waves, S-waves | Sound waves, P-waves, ultrasound waves |
| Polarization | Can be polarized | Cannot be polarized |
6.4 Polarization and Mechanical Waves
Polarization is a property of transverse waves that describes the direction of the oscillations. A polarized wave is one in which the oscillations occur in a single plane. Longitudinal waves cannot be polarized because their oscillations are parallel to the direction of propagation.
Polarization is used in various applications, such as:
- Sunglasses: Polarizing sunglasses reduce glare by blocking light waves that are polarized horizontally.
- 3D Movies: 3D glasses use polarization to separate the images for the left and right eyes, creating a sense of depth.
- LCD Screens: Liquid crystal displays (LCDs) use polarized light to create images.
7. Real-World Applications of the Wave Equation
The wave equation is a fundamental tool in physics and engineering, with numerous real-world applications.
7.1 Designing Musical Instruments Using the Wave Equation
The wave equation is essential for designing and understanding musical instruments. The frequencies at which an instrument vibrates are determined by the physical properties of the instrument, such as the length and tension of a string or the length and shape of an air column.
For example, the frequency of a vibrating string is given by:
f = (1/2L) √(T/μ)
Where:
- f is the frequency.
- L is the length of the string.
- T is the tension in the string.
- μ is the linear mass density of the string.
By manipulating these variables, instrument makers can create instruments that produce specific tones and harmonies.
7.2 Communication Systems and Wave Propagation
The wave equation is also crucial for understanding how electromagnetic waves propagate through communication systems. Radio waves, microwaves, and light waves are all used to transmit information over long distances.
Engineers use the wave equation to design antennas, waveguides, and other components that efficiently transmit and receive these waves. They also use the equation to predict how waves will be affected by the environment, such as atmospheric conditions or obstacles in the path.
7.3 Predicting Seismic Activity
Seismologists use the wave equation to study seismic waves and predict earthquakes. By analyzing the speed and direction of seismic waves, they can learn about the Earth’s interior structure and locate potential fault lines.
The wave equation also helps them understand how seismic waves will propagate through different types of rock and soil, allowing them to estimate the intensity of ground shaking at different locations during an earthquake.
7.4 Optimizing Acoustic Environments
The wave equation is used to optimize acoustic environments, such as concert halls and recording studios. By understanding how sound waves behave in a given space, architects and engineers can design rooms that minimize echoes and reverberations, creating a more pleasant listening experience.
They use the wave equation to predict how sound waves will reflect off surfaces, how they will be absorbed by different materials, and how they will interfere with each other. This allows them to create spaces that are optimized for sound quality.
8. Advanced Topics in Mechanical Waves
For those looking to delve deeper, there are several advanced topics in mechanical waves that are worth exploring.
8.1 Nonlinear Waves
Most of the discussion so far has focused on linear waves, where the amplitude of the wave is small compared to the wavelength. However, when the amplitude is large, the wave can become nonlinear, and the wave equation becomes more complex.
Nonlinear waves exhibit a variety of interesting phenomena, such as solitons (self-reinforcing waves that maintain their shape as they travel) and wave breaking (when a wave becomes too steep and collapses).
8.2 Damping and Attenuation
In real-world scenarios, mechanical waves are often subject to damping and attenuation, which reduce the amplitude of the wave as it travels. Damping is caused by friction or viscosity in the medium, while attenuation is caused by absorption or scattering of the wave energy.
Understanding damping and attenuation is essential for designing systems that use mechanical waves, such as sonar systems or acoustic devices.
8.3 Waveguides
A waveguide is a structure that guides waves, such as electromagnetic waves or sound waves. Waveguides are used in a variety of applications, such as microwave ovens, fiber optic cables, and acoustic horns.
The wave equation is used to design waveguides that efficiently transmit waves with minimal loss.
8.4 Metamaterials
Metamaterials are artificial materials that have properties not found in nature. They can be designed to manipulate waves in unusual ways, such as bending light backward or creating cloaking devices that hide objects from view.
Metamaterials are often used to control mechanical waves, creating devices that can absorb sound, focus ultrasound, or manipulate seismic waves.
9. Frequently Asked Questions (FAQ) about Mechanical Waves
To further clarify your understanding, here are some frequently asked questions about mechanical waves.
9.1 What is the main difference between mechanical and electromagnetic waves?
The main difference is that mechanical waves require a medium to travel, while electromagnetic waves do not. Electromagnetic waves can travel through a vacuum, like space, whereas mechanical waves need particles to vibrate.
9.2 Can mechanical waves travel through solids, liquids, and gases?
Yes, mechanical waves can travel through all three states of matter: solids, liquids, and gases. The speed of the wave varies depending on the medium.
9.3 How does temperature affect the speed of mechanical waves?
Generally, the speed of mechanical waves increases with temperature. This is because higher temperatures mean the particles in the medium have more kinetic energy and can transmit the wave more quickly.
9.4 What is the relationship between frequency and wavelength in mechanical waves?
The relationship is inverse and is described by the wave equation: v = fλ, where v is the wave speed, f is the frequency, and λ is the wavelength. If the frequency increases, the wavelength decreases, and vice versa, assuming the wave speed remains constant.
9.5 What happens when two mechanical waves meet?
When two mechanical waves meet, they interfere with each other. This interference can be constructive (where the amplitudes add together) or destructive (where the amplitudes cancel each other out).
9.6 How are mechanical waves used in medical imaging?
Mechanical waves, specifically ultrasound waves, are used in medical imaging to create images of internal body structures. The waves are emitted from a transducer, bounce off tissues, and the returning echoes are processed to form an image.
9.7 What is the role of mechanical waves in music?
Musical instruments use mechanical waves to produce sound. The vibration of strings, air columns, or drumheads creates sound waves that travel through the air to our ears.
9.8 How do earthquakes generate mechanical waves?
Earthquakes generate seismic waves, which are mechanical waves that travel through the Earth. These waves include P-waves (longitudinal) and S-waves (transverse).
9.9 Can mechanical waves be used for energy transfer?
Yes, mechanical waves can transfer energy. The amount of energy transferred is related to the amplitude of the wave; larger amplitudes mean more energy.
9.10 What are some advanced applications of mechanical waves?
Advanced applications include ultrasonic cleaning, material testing, welding, and the development of metamaterials that can manipulate waves in unusual ways.
10. Still Have Questions?
Mechanical waves are a fundamental aspect of physics and are essential for understanding many phenomena in our daily lives. By understanding the definition, types, characteristics, and applications of mechanical waves, you can gain a deeper appreciation for the world around you. Whether it’s understanding how sound travels or how earthquakes occur, mechanical waves play a vital role.
Have more questions about mechanical waves or any other topic? Don’t hesitate! Visit WHAT.EDU.VN now to ask your questions and get free answers from our community of experts.
Our address is 888 Question City Plaza, Seattle, WA 98101, United States. You can also reach us via WhatsApp at +1 (206) 555-7890 or visit our website at what.edu.vn. We’re here to help you understand the world better, one question at a time.