Centripetal force is the force that keeps an object moving along a circular path, and understanding it is essential in physics; let WHAT.EDU.VN be your guide. Grasp the concept of center-seeking force, explore real-world applications, and learn how to calculate it effectively. Delve into its significance in various fields such as astronomy, engineering, and even amusement park rides. Expand your knowledge with us as we uncover the intricacies of centripetal motion, circular motion, and Newton’s laws of motion.
1. Understanding Centripetal Force
Centripetal force is fundamental to understanding circular motion. It’s the force that compels an object to move along a circular path, constantly directed towards the center of the circle. Without it, objects would move in a straight line due to inertia.
1.1. Definition of Centripetal Force
Centripetal force is defined as the force that acts on a body moving in a circular path and is directed towards the center around which the body is moving. It is not a fundamental force like gravity or electromagnetism but rather a resultant force.
1.2. How Centripetal Force Works
Imagine whirling a ball attached to a string around your head. The tension in the string provides the centripetal force, constantly pulling the ball towards your hand (the center of the circle). This force changes the direction of the ball’s velocity, causing it to move in a circle rather than a straight line.
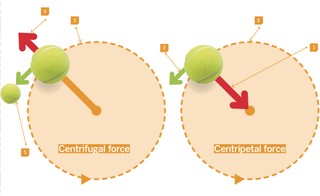
1.3. Relationship with Centrifugal Force
Centripetal force is often confused with centrifugal force, but they are distinct concepts. Centripetal force is a real force acting towards the center, while centrifugal force is a fictitious or apparent force that seems to push objects away from the center. The centrifugal effect is the result of inertia in a non-inertial (rotating) frame of reference.
1.4. Inertial Frame of Reference
An inertial frame of reference is a frame in which an object not subject to any net external force moves in a straight line at a constant speed or is at rest. Newton’s laws of motion are valid in inertial frames of reference. When observing circular motion from an inertial frame (a stationary point), only the centripetal force is considered a real force.
1.5. Non-Inertial Frame of Reference
A non-inertial frame of reference is one that is accelerating or rotating. In such frames, fictitious forces like the centrifugal force appear to act on objects. When observing circular motion from a rotating frame of reference, the centrifugal force seems real to the observer within that frame.
2. The Physics Behind Centripetal Force
The physics of centripetal force involves understanding Newton’s laws of motion and how they apply to circular motion. The key concepts include inertia, velocity, and acceleration.
2.1. Newton’s First Law and Inertia
Newton’s first law, the law of inertia, states that an object will remain at rest or in uniform motion in a straight line unless acted upon by an external force. In circular motion, the centripetal force is the external force that constantly changes the direction of the object’s velocity, preventing it from moving in a straight line.
2.2. Velocity and Acceleration in Circular Motion
In uniform circular motion, the speed of the object is constant, but its velocity is not because the direction is constantly changing. This change in velocity means the object is accelerating. The acceleration, known as centripetal acceleration, is always directed towards the center of the circle.
2.3. Centripetal Acceleration
Centripetal acceleration ((a_c)) is given by the formula:
[
a_c = frac{v^2}{r}
]
where:
- (v) is the speed of the object
- (r) is the radius of the circular path
This formula shows that the centripetal acceleration increases with the square of the speed and decreases with the radius of the circle.
2.4. Newton’s Second Law and Centripetal Force
Newton’s second law states that the force acting on an object is equal to the mass of the object multiplied by its acceleration ((F = ma)). In the case of centripetal force, this becomes:
[
F_c = m cdot a_c = m cdot frac{v^2}{r}
]
where:
- (F_c) is the centripetal force
- (m) is the mass of the object
- (v) is the speed of the object
- (r) is the radius of the circular path
This formula is crucial for calculating the magnitude of the centripetal force required to keep an object moving in a circle.
3. Calculating Centripetal Force
Calculating centripetal force involves using the formula (F_c = frac{mv^2}{r}). Understanding how to apply this formula is essential for solving problems related to circular motion.
3.1. The Centripetal Force Formula Explained
The formula (F_c = frac{mv^2}{r}) tells us that the centripetal force is directly proportional to the mass of the object and the square of its speed, and inversely proportional to the radius of the circular path.
- Mass ((m)): A heavier object requires a greater centripetal force to maintain the same speed and radius.
- Speed ((v)): Increasing the speed of the object significantly increases the required centripetal force because the force is proportional to the square of the speed.
- Radius ((r)): A smaller radius requires a greater centripetal force to keep the object moving in a circle.
3.2. Steps to Calculate Centripetal Force
- Identify the Variables: Determine the mass ((m)), speed ((v)), and radius ((r)) of the circular path. Ensure all units are consistent (e.g., kg for mass, m/s for speed, and meters for radius).
- Apply the Formula: Plug the values into the formula (F_c = frac{mv^2}{r}).
- Calculate the Force: Perform the calculation to find the centripetal force. The unit for force is Newtons (N).
3.3. Example Calculation
Suppose a 0.5 kg ball is whirled in a circle with a radius of 1 meter at a speed of 2 m/s. The centripetal force can be calculated as follows:
[
F_c = frac{mv^2}{r} = frac{0.5 cdot (2)^2}{1} = frac{0.5 cdot 4}{1} = 2 , text{N}
]
Therefore, the centripetal force required to keep the ball moving in a circle is 2 Newtons.
3.4. Common Mistakes to Avoid
- Unit Consistency: Ensure all values are in the correct units. Convert units if necessary.
- Squaring the Speed: Remember to square the speed ((v^2)) in the formula.
- Radius vs. Diameter: Use the radius, not the diameter, in the calculation.
- Direction of Force: Always remember that centripetal force is directed towards the center of the circle.
4. Real-World Examples of Centripetal Force
Centripetal force is evident in numerous real-world scenarios, from amusement park rides to celestial mechanics. Understanding these examples can help illustrate the practical applications of this force.
4.1. Circular Motion in Amusement Park Rides
Many amusement park rides rely on centripetal force to create thrilling experiences.
- Roller Coasters: As roller coasters go through loops, centripetal force, along with gravity, keeps the cars on the track.
- Merry-Go-Rounds: The seats on a merry-go-round move in a circle, with the centripetal force provided by the structure holding the seats.
- Gravitron: The Gravitron spins riders around a central axis, and the centripetal force presses them against the wall.
4.2. Centripetal Force in Vehicles
Vehicles utilize centripetal force to navigate turns.
- Cars on a Curved Road: When a car turns, friction between the tires and the road provides the centripetal force that keeps the car moving along the curved path.
- Airplanes Banking: Airplanes bank their wings to turn. The lift force of the wings provides the centripetal force needed for the turn.
4.3. Planetary Motion and Satellites
In celestial mechanics, centripetal force plays a crucial role.
- Planets Orbiting the Sun: The gravitational force between the sun and the planets provides the centripetal force that keeps the planets in their orbits.
- Satellites Orbiting Earth: Similarly, the gravitational force between Earth and satellites keeps the satellites in orbit.
4.4. Other Applications
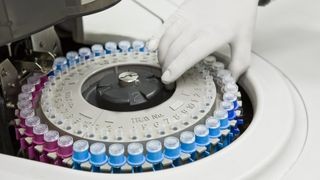
- Centrifuges: Used in laboratories to separate substances based on density. The centripetal force causes denser materials to move to the bottom of the tube.
4.5. The Physics of a Washing Machine
Ever wondered how your washing machine gets your clothes relatively dry after a wash? During the spin cycle, the drum rotates at high speed, and the clothes inside experience centripetal acceleration. The drum has small holes, and the water is forced out through these holes due to inertia, leaving your clothes damp rather than soaking wet.
5. The Role of Centripetal Force in Space Exploration
Centripetal force is essential for space exploration, influencing everything from satellite orbits to astronaut training. Understanding its effects is vital for designing missions and ensuring the safety of astronauts.
5.1. Maintaining Satellite Orbits
Satellites stay in orbit around Earth because of the balance between their inertia (tendency to move in a straight line) and the Earth’s gravitational pull. Gravity provides the centripetal force, constantly pulling the satellite towards Earth and forcing it to move in a circular or elliptical path. Without this force, the satellite would drift off into space.
5.2. Simulating Gravity in Space Stations
Creating artificial gravity in space stations is a significant challenge for long-duration space missions. One proposed solution is to rotate the space station. The centripetal force experienced by the astronauts due to the rotation would simulate the effect of gravity, helping to mitigate the adverse health effects of prolonged weightlessness, such as bone loss and muscle atrophy.
5.3. Astronaut Training with Centrifuges
Astronauts undergo rigorous training to prepare for the extreme accelerations they will experience during launch and re-entry. Large centrifuges are used to simulate these high-G forces. The centripetal force exerted by the centrifuge pushes the astronaut against the seat, replicating the sensation of intense acceleration.
5.4. Trajectory Calculations for Space Missions
Planning space missions requires precise calculations of trajectories to ensure spacecraft reach their destinations accurately. Centripetal force is a critical factor in these calculations, especially when dealing with orbital maneuvers and gravitational assists, where a spacecraft uses the gravity of a planet to alter its speed and direction.
5.5. Understanding Orbital Mechanics
Orbital mechanics, a branch of physics, deals with the motion of objects in space under the influence of gravity. Centripetal force is a fundamental concept in orbital mechanics, helping scientists and engineers understand and predict the behavior of satellites, planets, and other celestial bodies.
6. Centripetal Force vs. Centrifugal Force: Clearing the Confusion
Centripetal and centrifugal forces are often confused, but understanding the distinction between them is essential. Centripetal force is a real force that causes circular motion, while centrifugal force is an apparent force experienced in a rotating frame of reference.
6.1. Key Differences Explained
- Centripetal Force: A real force directed towards the center of the circle, causing an object to move in a circular path.
- Centrifugal Force: An apparent force that seems to push an object away from the center of the circle. It is a result of inertia in a non-inertial (rotating) frame of reference.
6.2. Frame of Reference Matters
The difference between centripetal and centrifugal force depends on the frame of reference:
- Inertial Frame: From a stationary point outside the rotating system, you observe the centripetal force pulling the object towards the center.
- Non-Inertial Frame: From the perspective of the rotating object, you experience the centrifugal force pushing you away from the center.
6.3. Example: Car Turning a Corner
Consider a car turning a corner:
- Inertial Frame (Observer outside the car): The friction between the tires and the road provides the centripetal force, causing the car to turn.
- Non-Inertial Frame (Driver inside the car): The driver feels a force pushing them towards the outside of the turn. This is the centrifugal force.
6.4. Why Centrifugal Force is Called “Fictitious”
Centrifugal force is considered a fictitious force because it is not a real force in the same way as gravity or electromagnetism. It arises solely from the fact that the observer is in an accelerating (rotating) frame of reference. In an inertial frame, only the centripetal force is needed to explain the motion.
6.5. Common Misconceptions
- Centrifugal force is not the “reaction” to centripetal force: According to Newton’s third law, forces always come in pairs, acting on different objects. The reaction to the centripetal force is the object’s inertia resisting the change in direction, not a force acting on the same object.
- Centrifugal force doesn’t “balance” centripetal force: In an inertial frame, only the centripetal force is needed to explain circular motion. Centrifugal force only appears in a rotating frame.
7. Advanced Concepts Related to Centripetal Force
Centripetal force is connected to several advanced concepts in physics, including rotational motion, angular velocity, and the Coriolis effect. Exploring these topics can provide a deeper understanding of centripetal force and its implications.
7.1. Rotational Motion and Angular Velocity
Rotational motion involves objects moving in a circular path around an axis. Angular velocity ((omega)) measures how fast an object is rotating, typically in radians per second. The relationship between linear velocity ((v)) and angular velocity is:
[
v = romega
]
where (r) is the radius of the circular path.
7.2. Torque and Angular Acceleration
Torque ((tau)) is the rotational equivalent of force and causes an object to undergo angular acceleration ((alpha)). The relationship between torque, moment of inertia ((I)), and angular acceleration is:
[
tau = Ialpha
]
These concepts are essential for understanding how forces cause rotational motion and how centripetal force fits into this broader context.
7.3. The Coriolis Effect
The Coriolis effect is an apparent deflection of moving objects when viewed from a rotating frame of reference. It is caused by the inertia of the object and the rotation of the frame. This effect is significant in meteorology, oceanography, and astronomy.
7.4. Moment of Inertia
Moment of inertia ((I)) is a measure of an object’s resistance to changes in its rotational motion. It depends on the object’s mass and how that mass is distributed relative to the axis of rotation. The greater the moment of inertia, the more torque is required to produce a given angular acceleration.
7.5. Applications in Engineering
These advanced concepts are crucial in engineering for designing rotating machinery, such as turbines, engines, and gyroscopes. Engineers must consider centripetal force, torque, and moment of inertia to ensure the safe and efficient operation of these devices.
8. Frequently Asked Questions (FAQs) About Centripetal Force
| Question | Answer |
|---|---|
| What exactly is centripetal force? | Centripetal force is the force that keeps an object moving along a circular path, directed towards the center of the circle. |
| How is centripetal force different from centrifugal force? | Centripetal force is a real force pulling an object towards the center, while centrifugal force is an apparent force pushing it away, experienced in a rotating frame of reference. |
| What is the formula for calculating centripetal force? | The formula is (F_c = frac{mv^2}{r}), where (F_c) is centripetal force, (m) is mass, (v) is speed, and (r) is the radius of the circular path. |
| Can you give a real-world example of centripetal force? | A car turning a corner: the friction between the tires and the road provides the centripetal force that keeps the car moving along the curved path. |
| What role does centripetal force play in space? | It keeps satellites in orbit around Earth and planets in orbit around the Sun, with gravity providing the necessary centripetal force. |
| Is centripetal force a fundamental force? | No, it is not a fundamental force like gravity or electromagnetism. It is a resultant force that arises from other forces acting on an object to cause circular motion. |
| What is centripetal acceleration? | Centripetal acceleration is the acceleration experienced by an object moving in a circular path, directed towards the center of the circle. It is calculated as (a_c = frac{v^2}{r}). |
| How does increasing speed affect centripetal force? | Increasing the speed of an object significantly increases the required centripetal force because the force is proportional to the square of the speed ((v^2)). |
| What happens if the centripetal force is removed? | If the centripetal force is removed, the object will no longer move in a circle and will instead move in a straight line tangent to the circle at the point where the force was removed, according to Newton’s first law of motion. |
| How do engineers use centripetal force in design? | Engineers use centripetal force principles to design roads, amusement park rides, and rotating machinery, ensuring safety and efficiency by accounting for the forces involved in circular motion. |
9. Further Exploration of Centripetal Force
For those seeking a deeper understanding of centripetal force, there are numerous resources available, including online courses, textbooks, and scientific articles.
9.1. Recommended Reading
- University Physics by Young and Freedman: A comprehensive textbook covering mechanics, including centripetal force.
- Fundamentals of Physics by Halliday, Resnick, and Walker: Another excellent textbook with detailed explanations and examples.
- HyperPhysics: A useful online resource with interactive diagrams and explanations of physics concepts.
9.2. Online Courses and Tutorials
- Khan Academy: Offers free lessons and exercises on physics, including circular motion and centripetal force.
- Coursera and edX: Provide university-level physics courses taught by experts in the field.
- YouTube Channels: Channels like “Physics Girl” and “Veritasium” offer engaging videos explaining physics concepts.
9.3. Interactive Simulations
- PhET Interactive Simulations: Offers interactive simulations for physics topics, including circular motion and centripetal force.
- The Physics Classroom: Provides simulations and tutorials on various physics concepts.
9.4. Experiments You Can Try at Home
- Whirling a Ball on a String: Tie a small ball to a string and whirl it around your head. Feel the tension in the string, which provides the centripetal force.
- Water in a Bucket: Fill a bucket with water and swing it in a vertical circle. Observe that the water stays in the bucket even when it’s upside down, thanks to centripetal force.
- Toy Car on a Circular Track: Set up a circular track for a toy car and observe how the car stays on the track due to the centripetal force provided by the track.
10. Why Understanding Centripetal Force Matters
Understanding centripetal force is not just an academic exercise; it has practical implications in various fields and everyday life.
10.1. Importance in Physics Education
Centripetal force is a fundamental concept in physics that helps students understand the laws of motion, gravity, and circular motion. It forms the basis for more advanced topics like rotational dynamics and orbital mechanics.
10.2. Applications in Engineering and Technology
Engineers use centripetal force principles to design safe and efficient systems, from roads and bridges to aircraft and spacecraft. Understanding this force is crucial for ensuring the stability and performance of these structures.
10.3. Relevance to Everyday Life
Centripetal force affects many aspects of everyday life, from driving a car to riding a bicycle. Understanding how it works can help you make informed decisions and stay safe in various situations.
10.4. Encouraging Curiosity and Exploration
Learning about centripetal force can spark curiosity and encourage further exploration of the natural world. It can inspire students to pursue careers in science, technology, engineering, and mathematics (STEM) fields.
10.5. Addressing Common Misconceptions
By understanding centripetal force, people can avoid common misconceptions about motion and forces, leading to a more accurate understanding of how the world works.
Navigating the world of physics can be challenging, but you don’t have to do it alone. At WHAT.EDU.VN, we understand the difficulties in finding quick, reliable answers to your questions. Whether you’re a student tackling homework, a professional seeking clarity, or simply a curious mind eager to learn, our platform offers a free and easy way to get the answers you need.
Are you struggling to grasp the nuances of centripetal force or any other complex topic? Do you find yourself spending hours searching for reliable information without success? WHAT.EDU.VN is here to help. We provide a space where you can ask any question and receive prompt, accurate responses from knowledgeable individuals.
Don’t let your questions go unanswered. Join the WHAT.EDU.VN community today and experience the ease of getting the information you need, absolutely free. Simply visit our website at WHAT.EDU.VN, type in your question, and let our experts guide you. For any inquiries, feel free to reach us at 888 Question City Plaza, Seattle, WA 98101, United States, or connect with us on WhatsApp at +1 (206) 555-7890. what.edu.vn is your go-to resource for all your questions.

