What Is A Point Of Inflection: Definition And Examples

What Is A Point Of Inflection? It’s a crucial concept in calculus, and WHAT.EDU.VN is here to make it crystal clear. Delve into understanding how to identify points of inflection, explore their significance, and see real-world applications. Learn about concavity, derivatives, and inflection points – all essential for mastering calculus and related fields. Let us help you find stationary points and understand derivative tests today.

1. Understanding the Inflection Point Definition

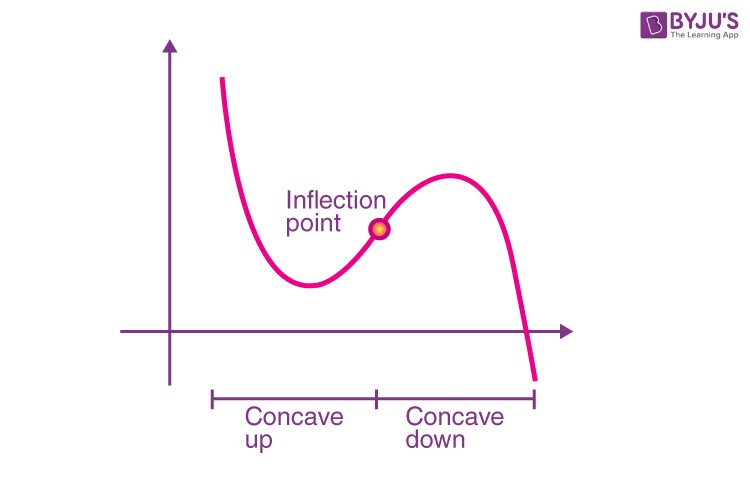
An inflection point, also known as a point of inflection or flex, marks a spot on a curve where the concavity shifts. Imagine a road that curves: an inflection point is where the curve changes from bending left to bending right, or vice versa. Mathematically, this means the function transitions from being concave up to concave down, or the reverse. Discover more educational resources at WHAT.EDU.VN.

Think of it like this:

Concave Up: Like a smile, holding water.
Concave Down: Like a frown, spilling water.

The inflection point is the exact spot where the smile turns into a frown or the frown turns into a smile. It’s not a maximum or minimum point (those are local extrema), but rather a point of change.

2. Concavity Explained

Concavity describes the direction in which a curve bends. A function can be concave up, concave down, or neither (at an inflection point). Understanding concavity is crucial for analyzing the behavior of functions. WHAT.EDU.VN offers resources to help you grasp these concepts effectively.

Concave Up (Convex Down): The curve opens upwards. A tangent line at any point on the curve lies below the curve itself (except at the point of tangency).
Concave Down (Convex Up): The curve opens downwards. A tangent line at any point on the curve lies above the curve itself (except at the point of tangency).

3. The Calculus Behind Inflection Points

Calculus provides the tools to precisely identify inflection points. The key is the second derivative of the function. Explore calculus concepts and get your questions answered for free at WHAT.EDU.VN.

Second Derivative: The rate of change of the rate of change (the derivative of the derivative). It tells us about the concavity of the function.
f”(x) > 0: Function is concave up.
f”(x) < 0: Function is concave down.
f”(x) = 0 or Undefined: Potential inflection point. We need to further investigate.

To find inflection points:

Find the second derivative of the function, f”(x).
Set f”(x) = 0 and solve for x. These are potential inflection points.
Check the sign of f”(x) on either side of each potential inflection point. If the sign changes, then it is indeed an inflection point. If the sign does not change, it is not an inflection point.

4. Visualizing Inflection Points on a Graph

Graphs provide a clear visual representation of inflection points. Look for points where the curve changes its “bend.” You can easily grasp the concept of inflection points with clear explanations at WHAT.EDU.VN.

Key things to look for:

Change in Concavity: The most obvious visual cue. The curve switches from looking like a cup to a cap, or vice versa.
Tangent Line Behavior: Imagine drawing tangent lines along the curve. At an inflection point, the tangent line will cross the curve (rather than just touching it).

5. Stationary vs. Non-Stationary Inflection Points

Inflection points can be further classified based on the value of the first derivative at that point. This distinction helps us understand the behavior of the function at the point of inflection. Ask your burning questions and receive reliable answers at WHAT.EDU.VN.

Stationary Inflection Point: The first derivative, f'(x), is equal to zero. This means the tangent line at the inflection point is horizontal. The function momentarily “flattens out” before changing concavity.
Non-Stationary Inflection Point: The first derivative, f'(x), is not equal to zero. The tangent line at the inflection point is not horizontal. The function is still increasing or decreasing as it changes concavity.

6. Finding Inflection Points: A Step-by-Step Guide

Let’s formalize the process of finding inflection points with a clear set of steps. We will explore the point of the second derivative and how it helps with identifying concavity change.

Find the Second Derivative: Calculate f”(x) from the original function f(x). This is often the most challenging step, requiring a good understanding of differentiation rules.
Set the Second Derivative to Zero: Solve the equation f”(x) = 0 for x. This will give you the x-coordinates of the potential inflection points. It’s also crucial to identify where f”(x) is undefined, as these points can also be inflection points.
Test Intervals: Create a number line with the potential inflection points marked. Choose a test value within each interval and plug it into f”(x). Determine the sign of f”(x) in each interval.
Determine Inflection Points: Analyze the sign changes of f”(x). If the sign changes at a potential inflection point, then it is indeed an inflection point. If the sign does not change, it is not.
Find the y-coordinate: For each inflection point (x-coordinate), plug the x-value back into the original function f(x) to find the corresponding y-coordinate. This gives you the complete coordinates (x, y) of the inflection point.

7. Inflection Point Examples: Working Through Problems

Let’s illustrate the process with some examples. These examples cover different types of functions and demonstrate the application of the steps outlined above.

Example 1: Polynomial Function

Find the inflection points of f(x) = x³ – 6x² + 5x – 10

Find the Second Derivative:
- f'(x) = 3x² – 12x + 5
- f”(x) = 6x – 12
Set the Second Derivative to Zero:
- 6x – 12 = 0
- 6x = 12
- x = 2
Test Intervals:
- Interval 1: x < 2. Choose x = 0. f”(0) = 6(0) – 12 = -12 (Negative)
- Interval 2: x > 2. Choose x = 3. f”(3) = 6(3) – 12 = 6 (Positive)
Determine Inflection Points:
- The sign of f”(x) changes at x = 2. Therefore, x = 2 is an inflection point.
Find the y-coordinate:
- f(2) = (2)³ – 6(2)² + 5(2) – 10 = 8 – 24 + 10 – 10 = -16
- The inflection point is (2, -16).

Example 2: Rational Function

Find the inflection points of f(x) = x / (x² + 1)

Find the Second Derivative:
- f'(x) = (1 – x²) / (x² + 1)²
- f”(x) = (2x(x² – 3)) / (x² + 1)³
Set the Second Derivative to Zero:
- 2x(x² – 3) = 0
- x = 0 or x² – 3 = 0
- x = 0, x = √3, x = -√3
Test Intervals: (This is a bit more involved due to the three potential inflection points. You would need to test intervals like x < -√3, -√3 < x < 0, 0 < x < √3, and x > √3)
Determine Inflection Points: (After testing the intervals, you would find that all three points are indeed inflection points).
Find the y-coordinate:
- f(0) = 0 / (0² + 1) = 0
- f(√3) = √3 / ((√3)² + 1) = √3 / 4
- f(-√3) = -√3 / ((-√3)² + 1) = -√3 / 4
- The inflection points are (0, 0), (√3, √3 / 4), and (-√3, -√3 / 4).

Example 3: Trigonometric Function

Find the inflection points of f(x) = sin(x) on the interval [0, 2π]

Find the Second Derivative:
- f'(x) = cos(x)
- f”(x) = -sin(x)
Set the Second Derivative to Zero:
- -sin(x) = 0
- x = 0, π, 2π (within the interval [0, 2π])
Test Intervals:
- Interval 1: 0 < x < π. Choose x = π/2. f”(π/2) = -sin(π/2) = -1 (Negative)
- Interval 2: π < x < 2π. Choose x = 3π/2. f”(3π/2) = -sin(3π/2) = 1 (Positive)
Determine Inflection Points:
- The sign of f”(x) changes at x = π. Therefore, x = π is an inflection point.
- Although f”(0) = 0 and f”(2π) = 0, these are endpoints of the interval and concavity doesn’t change around them within the interval. So they aren’t considered inflection points in this context.
Find the y-coordinate:
- f(π) = sin(π) = 0
- The inflection point is (π, 0).

8. Real-World Applications of Inflection Points

Inflection points aren’t just abstract mathematical concepts. They have practical applications in various fields. Find valuable insights and learn about a variety of topics on WHAT.EDU.VN.

Economics: In cost curves, the inflection point represents the point of diminishing returns. After this point, increasing inputs yields smaller increases in output.
Physics: In physics, inflection points can represent changes in acceleration or other rates of change.
Statistics: In statistics, inflection points can help identify changes in the rate of growth or decay in data sets.
Engineering: Engineers use inflection points to analyze the stability and behavior of structures and systems.
Machine Learning: Inflection points help determine model behavior, especially in activation functions within neural networks.

9. Common Mistakes to Avoid

Finding inflection points can be tricky. Here are some common mistakes to watch out for. Consult WHAT.EDU.VN for expert assistance and reliable information.

Assuming f”(x) = 0 Guarantees an Inflection Point: This is not always the case. You must check for a sign change in f”(x) around the point.
Forgetting to Check Where f”(x) is Undefined: Inflection points can occur where the second derivative is undefined, such as at a vertical asymptote.
Confusing Inflection Points with Local Maxima or Minima: Inflection points are points of changing concavity, while local maxima and minima are turning points.
Incorrectly Calculating Derivatives: A mistake in calculating the first or second derivative will lead to incorrect results. Double-check your work!

10. Inflection Points and Curve Sketching

Inflection points are powerful tools for sketching accurate graphs of functions. By identifying inflection points, along with other key features like intercepts, asymptotes, and local extrema, you can create a detailed representation of the function’s behavior. Do you have questions? Ask them on WHAT.EDU.VN and get reliable answers.

Here’s how inflection points contribute to curve sketching:

Identify Key Features: Find intercepts (where the graph crosses the x and y axes), asymptotes (lines the graph approaches), and local maxima/minima (turning points).
Find Inflection Points: Use the steps outlined earlier to find the inflection points.
Determine Concavity: Use the second derivative to determine the intervals where the function is concave up or concave down.
Sketch the Graph: Plot the key features and inflection points. Use the concavity information to sketch the shape of the curve in each interval. Connect the points smoothly, ensuring the curve changes concavity at the inflection points.

11. The Significance of the Second Derivative Test

The second derivative test is a powerful tool in calculus that uses the second derivative of a function to determine whether a critical point (where the first derivative is zero or undefined) is a local maximum, a local minimum, or neither. Inflection points are crucial for understanding how the second derivative test helps in curve sketching.

If f”(c) > 0, then f(x) has a local minimum at x = c.
If f”(c) < 0, then f(x) has a local maximum at x = c.
If f”(c) = 0, the test is inconclusive. It could be an inflection point or neither a maximum nor a minimum.

12. Advanced Concepts Related to Inflection Points

While the basic definition of an inflection point is straightforward, there are more advanced concepts to explore. Learn more about advanced mathematical concepts at WHAT.EDU.VN.

Saddle Points: In multivariable calculus, saddle points are analogous to inflection points. They are points where the function is neither a maximum nor a minimum but changes concavity in different directions.
Higher-Order Derivatives: Analyzing higher-order derivatives can provide even more detailed information about the behavior of a function, including the rate of change of concavity.
Applications in Optimization: Inflection points can play a role in optimization problems, helping to identify optimal solutions or regions of interest.

13. Inflection Points in Discrete Mathematics

While inflection points are typically discussed in the context of continuous functions in calculus, the concept can be extended to discrete mathematics. In discrete settings, we look for changes in the “trend” or “pattern” of a sequence or data set.

For example, in a sequence of numbers, an inflection point might be a point where the rate of increase or decrease changes significantly. This can be useful in analyzing trends in data, such as stock prices or population growth.

14. Numerical Methods for Finding Inflection Points

In many real-world applications, finding inflection points analytically (using calculus) can be difficult or impossible. In these cases, numerical methods can be used to approximate the location of inflection points.

Some common numerical methods include:

Finite Difference Methods: Approximating the derivatives using finite differences.
Root-Finding Algorithms: Using algorithms like the Newton-Raphson method to find the roots of the second derivative.
Optimization Techniques: Using optimization techniques to find points where the second derivative changes sign.

15. How Technology Aids in Inflection Point Analysis

Technology can greatly simplify the process of finding and analyzing inflection points. Numerous software tools and online calculators are available to help.

Graphing Calculators: Graphing calculators can plot functions and visually identify inflection points.
Computer Algebra Systems (CAS): Software like Mathematica, Maple, and SymPy can calculate derivatives and solve equations symbolically, making it easier to find inflection points analytically.
Online Calculators: Many online calculators can find derivatives and inflection points with minimal input.

16. The Role of Inflection Points in Optimization Problems

Inflection points play a crucial role in optimization problems, especially in determining the nature of critical points and understanding the behavior of the function around those points. Optimization problems involve finding the maximum or minimum value of a function, often subject to certain constraints.

Identifying Potential Optima: Inflection points can help identify potential locations where the function might reach its maximum or minimum values.
Understanding Function Behavior: By analyzing the concavity of the function using inflection points, we can gain insights into how the function behaves and where it is likely to reach its optimal values.
Constrained Optimization: In constrained optimization problems, inflection points can help determine whether a critical point satisfies the constraints and whether it corresponds to a maximum or minimum value.

17. Exploring Inflection Points in Different Types of Functions

Inflection points can manifest differently in various types of functions, each with its unique characteristics and applications. Let’s delve into some common function types and how inflection points behave in each.

Polynomial Functions: These are functions of the form f(x) = an x^n + a{n-1} x^{n-1} + … + a_1 x + a_0, where a_i are constants and n is a non-negative integer. Polynomial functions can have multiple inflection points, and their behavior is often determined by the degree of the polynomial.
Rational Functions: These are functions of the form f(x) = P(x) / Q(x), where P(x) and Q(x) are polynomial functions. Rational functions can have inflection points, vertical asymptotes, and horizontal asymptotes, which can affect their concavity and behavior.
Trigonometric Functions: These functions, such as sine, cosine, and tangent, are periodic and oscillate between certain values. Trigonometric functions can have inflection points at regular intervals, reflecting their periodic nature.
Exponential Functions: These functions, such as f(x) = a^x, where a is a constant, exhibit exponential growth or decay. Exponential functions typically do not have inflection points, as their concavity remains constant.
Logarithmic Functions: These functions, such as f(x) = log_a(x), are the inverse of exponential functions. Logarithmic functions can have inflection points, and their concavity changes depending on the base of the logarithm.

18. Practical Exercises to Master Inflection Points

Mastering the concept of inflection points requires practice. Here are some practical exercises to help you solidify your understanding:

Find Inflection Points of Polynomial Functions:
- f(x) = x^3 – 3x^2 + 2x – 1
- f(x) = x^4 – 6x^2 + 8x + 10
Find Inflection Points of Rational Functions:
- f(x) = (x + 1) / (x – 2)
- f(x) = x^2 / (x^2 + 1)
Find Inflection Points of Trigonometric Functions:
- f(x) = sin(2x)
- f(x) = cos(x) + sin(x)
Analyze Real-World Data:
- Find data sets related to economics, physics, or statistics and identify potential inflection points in the data.
- Interpret the meaning of these inflection points in the context of the data.

19. Addressing Common Misconceptions About Inflection Points

Despite their importance, several misconceptions surround inflection points. Let’s address some of the most common ones:

Inflection Points Are Always Turning Points: This is not true. Inflection points are points where the concavity changes, not necessarily where the function changes direction.
The Second Derivative Must Be Zero at an Inflection Point: While the second derivative is often zero at an inflection point, it can also be undefined.
Inflection Points Only Exist in Continuous Functions: The concept of inflection points can be extended to discrete functions and data sets, where we look for changes in the trend or pattern.
Inflection Points Are Only Useful in Mathematics: Inflection points have practical applications in various fields, including economics, physics, statistics, engineering, and machine learning.

20. The Future of Inflection Point Analysis

As technology and mathematics continue to advance, the future of inflection point analysis is bright. New tools and techniques are being developed to make it easier to find and analyze inflection points, and new applications are being discovered in various fields.

Some potential future developments include:

AI-Powered Inflection Point Analysis: Artificial intelligence (AI) and machine learning (ML) algorithms could be used to automate the process of finding and analyzing inflection points in complex data sets.
Integration with Data Visualization Tools: Inflection point analysis could be integrated with data visualization tools to provide more intuitive and insightful representations of data trends.
Applications in Emerging Fields: Inflection point analysis could find new applications in emerging fields such as bioinformatics, climate science, and financial modeling.

Do you still have questions about inflection points or other mathematical concepts? Don’t hesitate to ask on WHAT.EDU.VN. Our community of experts is ready to provide you with clear and helpful answers, completely free of charge. We’re located at 888 Question City Plaza, Seattle, WA 98101, United States. You can also reach us via WhatsApp at +1 (206) 555-7890 or visit our website at WHAT.EDU.VN. Let WHAT.EDU.VN be your trusted resource for all your learning needs. We’re here to help you succeed!

Why struggle with complex concepts when you can get the answers you need quickly and easily? Visit what.edu.vn today and ask your question!