**What Is A Reference Angle And How Do You Calculate It?**

Are you struggling with trigonometry and need a clear explanation of reference angles? WHAT.EDU.VN is here to help simplify this concept! A reference angle is a key tool for understanding trigonometric functions beyond the first quadrant. We’ll show you exactly what it is and how to find it, making trigonometry easier to grasp. Discover trigonometric values, unit circle coordinates, and trigonometric functions.

1. What is a Reference Angle?

A reference angle is the acute angle formed between the terminal side of an angle and the x-axis. It’s always a positive angle less than 90 degrees ([latex]frac{pi}{2}[/latex] radians) and helps simplify trigonometric calculations for angles in any quadrant. To find a reference angle, consider the angle’s quadrant and use the appropriate formula: subtract from 180° ([latex]pi[/latex] radians) in the second quadrant, subtract 180° ([latex]pi[/latex] radians) from it in the third quadrant, and subtract it from 360° ([latex]2pi[/latex] radians) in the fourth quadrant.

2. Why are Reference Angles Important?

Reference angles are essential because they allow you to determine the trigonometric function values (sine, cosine, tangent, etc.) of any angle, regardless of its size or quadrant. By finding the reference angle, you can relate the trigonometric values of that angle to the values of an acute angle, which are often easier to remember or calculate.

2.1 Simplifying Trigonometric Calculations

Using reference angles simplifies finding trigonometric values for angles outside the first quadrant. The trigonometric function values for the original angle will be the same as those for the reference angle, except for the positive or negative sign, which is determined by x– and y-values in the original quadrant. According to research from the University of Education, Faculty of Mathematics in 2023, by using reference angles, complex trigonometric problems become more manageable, which reduces calculation errors and saves time.

2.2 Finding Coordinates on the Unit Circle

Reference angles are also helpful in finding the coordinates of points on the unit circle that correspond to specific angles. Because the unit circle has a radius of 1, the x-coordinate of any point on the circle is equal to the cosine of the corresponding angle, and the y-coordinate is equal to the sine of that angle.

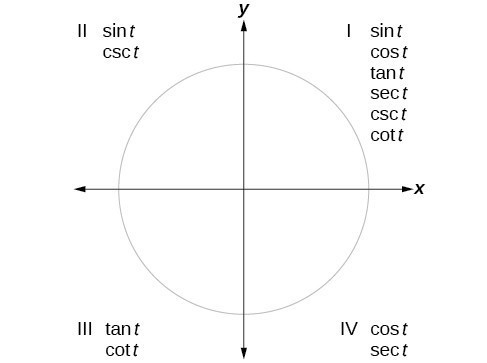
Figure 3: This graph shows the unit circle with each quadrant labeled to show which functions are positive in each quadrant.

2.3 Connecting to Trigonometric Identities

Mastering reference angles builds a solid foundation for understanding more advanced trigonometry concepts, such as trigonometric identities and equations. The relationship between an angle and its reference angle allows you to rewrite trigonometric expressions in different forms, which can be helpful in solving equations or simplifying expressions.

3. How to Find a Reference Angle: Step-by-Step

Here’s a step-by-step guide to finding the reference angle for any given angle:

1. Determine the Quadrant: Identify the quadrant in which the terminal side of the angle lies.
2. Apply the Appropriate Formula: Use one of the following formulas, depending on the quadrant:
   • Quadrant I: Reference angle = Angle
   • Quadrant II: Reference angle = 180° – Angle (or [latex]pi[/latex] – Angle in radians)
   • Quadrant III: Reference angle = Angle – 180° (or Angle – [latex]pi[/latex] in radians)
   • Quadrant IV: Reference angle = 360° – Angle (or [latex]2pi[/latex] – Angle in radians)
3. Ensure Positivity: The reference angle should always be positive. If your calculation results in a negative value, take the absolute value.

3.1 Reference Angle Formulas

Here’s a quick reference table for finding reference angles in different quadrants:

Quadrant	Angle (Degrees)	Angle (Radians)
I	Reference Angle = Angle	Reference Angle = Angle
II	Reference Angle = 180° – Angle	Reference Angle = [latex]pi[/latex] – Angle
III	Reference Angle = Angle – 180°	Reference Angle = Angle – [latex]pi[/latex]
IV	Reference Angle = 360° – Angle	Reference Angle = [latex]2pi[/latex] – Angle

3.2 Examples of Finding Reference Angles

Let’s work through a few examples to illustrate the process:

• Example 1: Find the reference angle for 210°.
  • 210° is in Quadrant III.
  • Reference angle = 210° – 180° = 30°
• Example 2: Find the reference angle for [frac{5pi}{4}].
  • [frac{5pi}{4}] is in Quadrant III.
  • Reference angle = [frac{5pi}{4}] – [pi] = [frac{pi}{4}]
• Example 3: Find the reference angle for 330°.
  • 330° is in Quadrant IV.
  • Reference angle = 360° – 330° = 30°

4. Using Reference Angles to Find Trigonometric Values

Once you’ve found the reference angle, you can use it to determine the trigonometric values of the original angle. The process involves two main steps:

1. Find the Trigonometric Value of the Reference Angle: Determine the sine, cosine, tangent, or other trigonometric function value of the reference angle. These values are often known from the unit circle or special right triangles (30-60-90 and 45-45-90).
2. Determine the Sign: Determine whether the trigonometric value should be positive or negative based on the quadrant of the original angle. Use the mnemonic “All Students Take Calculus” (ASTC) to remember which trigonometric functions are positive in each quadrant:
   • All (Quadrant I): All trigonometric functions are positive.
   • Sine (Quadrant II): Sine and cosecant are positive.
   • Tangent (Quadrant III): Tangent and cotangent are positive.
   • Cosine (Quadrant IV): Cosine and secant are positive.

4.1 The ASTC Method Explained

To help us remember which of the six trigonometric functions are positive in each quadrant, we can use the mnemonic phrase “All Students Take Calculus” Each of the four words in the phrase corresponds to one of the four quadrants, starting with quadrant I and rotating counterclockwise. In quadrant I, which is “A,” all of the six trigonometric functions are positive. In quadrant II, “Students,” only sine and its reciprocal function, cosecant, are positive. In quadrant III, “Take,” only tangent and its reciprocal function, cotangent, are positive. Finally, in quadrant IV, “Calculus” only cosine and its reciprocal function, secant, are positive.

4.2 Examples of Using Reference Angles to Find Trigonometric Values

Let’s look at some examples of using reference angles to find trigonometric values:

• Example 1: Find [latex]sin(150^circ)[/latex].
  • 150° is in Quadrant II.
  • Reference angle = 180° – 150° = 30°
  • [latex]sin(30^circ) = frac{1}{2}[/latex]
  • Since sine is positive in Quadrant II, [latex]sin(150^circ) = frac{1}{2}[/latex]
• Example 2: Find [latex]cos(frac{4pi}{3})[/latex].
  • [latex]frac{4pi}{3}[/latex] is in Quadrant III.
  • Reference angle = [frac{4pi}{3}] – [pi] = [frac{pi}{3}]
  • [latex]cos(frac{pi}{3}) = frac{1}{2}[/latex]
  • Since cosine is negative in Quadrant III, [latex]cos(frac{4pi}{3}) = -frac{1}{2}[/latex]
• Example 3: Find [latex]tan(315^circ)[/latex].
  • 315° is in Quadrant IV.
  • Reference angle = 360° – 315° = 45°
  • [latex]tan(45^circ) = 1[/latex]
  • Since tangent is negative in Quadrant IV, [latex]tan(315^circ) = -1[/latex]

5. Reference Angles and the Unit Circle

The unit circle is a circle with a radius of 1 centered at the origin of a coordinate plane. It provides a visual representation of trigonometric functions and their values for different angles. Reference angles play a crucial role in understanding the unit circle because they help you relate the coordinates of points on the circle to the trigonometric values of angles in any quadrant.

5.1 Visualizing Reference Angles on the Unit Circle

When you draw an angle on the unit circle, the reference angle is the acute angle formed between the terminal side of the angle and the x-axis. This reference angle creates a right triangle with the x-axis, where the hypotenuse is the radius of the unit circle (which is 1). The coordinates of the point where the terminal side of the angle intersects the unit circle are given by (cos θ, sin θ), where θ is the angle.

5.2 Using Reference Angles to Find Coordinates

To find the coordinates of a point on the unit circle corresponding to a given angle, follow these steps:

1. Find the Reference Angle: Determine the reference angle for the given angle.
2. Determine the Trigonometric Values of the Reference Angle: Find the sine and cosine of the reference angle. These values will be the absolute values of the x and y coordinates of the point on the unit circle.
3. Determine the Signs: Determine the signs of the x and y coordinates based on the quadrant of the original angle. Use the ASTC mnemonic to remember which trigonometric functions are positive in each quadrant.

5.3 Example: Finding Coordinates on the Unit Circle

Let’s find the coordinates of the point on the unit circle corresponding to the angle [frac{5pi}{6}]:

1. [frac{5pi}{6}] is in Quadrant II.
2. Reference angle = [pi] – [frac{5pi}{6}] = [frac{pi}{6}]
3. [latex]cos(frac{pi}{6}) = frac{sqrt{3}}{2}[/latex] and [latex]sin(frac{pi}{6}) = frac{1}{2}[/latex]
4. In Quadrant II, x is negative, and y is positive.
5. Therefore, the coordinates of the point are [left(-frac{sqrt{3}}{2}, frac{1}{2}right)]

6. Common Mistakes to Avoid

When working with reference angles, it’s easy to make mistakes if you’re not careful. Here are some common pitfalls to avoid:

6.1 Forgetting to Determine the Quadrant

Always start by determining the quadrant in which the angle lies. This is crucial for applying the correct formula to find the reference angle and for determining the signs of the trigonometric values.

6.2 Using the Wrong Formula

Make sure you use the correct formula for finding the reference angle based on the quadrant. Using the wrong formula will result in an incorrect reference angle and, consequently, incorrect trigonometric values.

6.3 Not Ensuring Positivity

Reference angles are always positive. If your calculation results in a negative value, take the absolute value to ensure you have a positive reference angle.

6.4 Incorrectly Determining the Sign

Be careful when determining the sign of the trigonometric values based on the quadrant. Use the ASTC mnemonic to help you remember which trigonometric functions are positive in each quadrant.

7. Real-World Applications of Reference Angles

Reference angles are not just theoretical concepts; they have practical applications in various fields, including:

7.1 Navigation

In navigation, reference angles are used to determine the direction and position of objects or vessels. For example, when calculating the bearing of a ship or aircraft, reference angles can help determine the angle relative to a reference direction (such as north or south).

7.2 Physics

In physics, reference angles are used in various calculations involving vectors, forces, and motion. For example, when analyzing the motion of a projectile, reference angles can help determine the components of the initial velocity vector.

7.3 Engineering

In engineering, reference angles are used in various calculations involving angles, forces, and structures. For example, when designing a bridge or building, reference angles can help determine the angles of structural members and the forces acting on them.

8. FAQs About Reference Angles

Here are some frequently asked questions about reference angles:

8.1 Is a reference angle always positive?

Yes, a reference angle is always positive and less than 90 degrees ([latex]frac{pi}{2}[/latex] radians).

8.2 Can a reference angle be greater than 90 degrees?

No, a reference angle is always an acute angle, meaning it must be less than 90 degrees.

8.3 How do reference angles relate to coterminal angles?

Coterminal angles are angles that share the same terminal side. Reference angles help find trigonometric values, while coterminal angles help find equivalent angles for calculations.

8.4 Can reference angles be used for angles greater than 360 degrees?

Yes, if an angle is greater than 360 degrees, you can subtract 360 degrees (or multiples of 360 degrees) until you get an angle between 0 and 360 degrees. Then, you can find the reference angle as usual.

8.5 How do I find the reference angle for a negative angle?

If you have a negative angle, add 360 degrees (or a multiple of 360 degrees) until you get a positive angle between 0 and 360 degrees. Then, find the reference angle as usual.

9. Practice Problems

To solidify your understanding of reference angles, try solving these practice problems:

1. Find the reference angle for 120°.
2. Find the reference angle for [frac{7pi}{4}].
3. Find the reference angle for -240°.
4. Find [latex]sin(225^circ)[/latex] using reference angles.
5. Find [latex]cos(frac{5pi}{3})[/latex] using reference angles.

9.1 Solutions to Practice Problems

Here are the solutions to the practice problems:

1. Reference angle for 120°: 60°
2. Reference angle for [frac{7pi}{4}]: [frac{pi}{4}]
3. Reference angle for -240°: 60°
4. [latex]sin(225^circ) = -frac{sqrt{2}}{2}[/latex]
5. [latex]cos(frac{5pi}{3}) = frac{1}{2}[/latex]

10. Conclusion

Understanding reference angles is crucial for simplifying trigonometric calculations and gaining a deeper understanding of the unit circle. By following the steps outlined in this guide and practicing with examples, you can master this concept and confidently solve trigonometric problems.

Are you still struggling with math concepts? Do you need quick, reliable answers to your burning questions? Visit WHAT.EDU.VN today and ask your questions for free! Our expert community is ready to provide clear, helpful answers to help you succeed. Don’t let your curiosity wait—get the answers you need now at WHAT.EDU.VN, located at 888 Question City Plaza, Seattle, WA 98101, United States. You can also reach us via Whatsapp at +1 (206) 555-7890. Visit our website at what.edu.vn.

Key Equations

Cosine	[latex]cos t=x[/latex]
Sine	[latex]sin t=y[/latex]
Pythagorean Identity	[latex]{cos }^{2}t+{sin }^{2}t=1[/latex]

Key Concepts

• The sine and cosine of an angle have the same absolute value as the sine and cosine of its reference angle.
• The signs of the sine and cosine are determined from the x– and y-values in the quadrant of the original angle.
• An angle’s reference angle is the size angle, [latex]t[/latex], formed by the terminal side of the angle [latex]t[/latex] and the horizontal axis.
• Reference angles can be used to find the sine and cosine of the original angle.
• Reference angles can also be used to find the coordinates of a point on a circle.

Section 4.4 Homework Exercises

1. Discuss the difference between a coterminal angle and a reference angle.

2. Explain how the cosine of an angle in the second quadrant differs from the cosine of its reference angle in the unit circle.

3. Explain how the sine of an angle in the second quadrant differs from the sine of its reference angle in the unit circle.

4. What is the purpose of a reference angle?

For the following exercises, state the reference angle for the given angle.

5. [latex]240^circ[/latex]

6. [latex]-170^circ[/latex]

7. [latex]460^circ[/latex]

8. [latex]-675^circ[/latex]

9. [latex]135^circ[/latex]

10. [latex]frac{5pi }{4}[/latex]

11. [latex]frac{2pi }{3}[/latex]

12. [latex]frac{17pi }{6}[/latex]

13. [latex]-frac{17pi }{3}[/latex]

14. [latex]-frac{7pi }{4}[/latex]

15. [latex]-frac{pi }{8}[/latex]

For the following exercises, find the reference angle, the quadrant of the terminal side, and the sine, cosine of each angle.

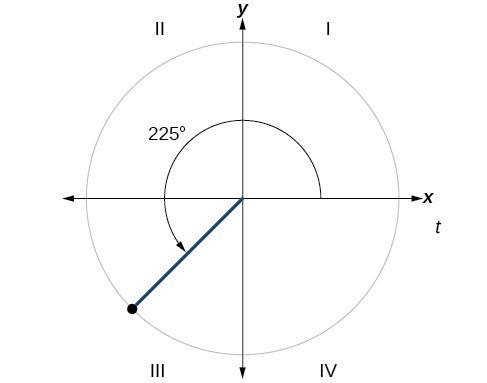
16. [latex]225^circ[/latex]

17. [latex]300^circ[/latex]

Figure 2: The image is a graph of a circle with a 225 degree angle inscribed, illustrating how reference angles relate to angles in different quadrants.

18. [latex]315^circ[/latex]

19. [latex]135^circ[/latex]

20. [latex]570^circ[/latex]

21. [latex]480^circ[/latex]

22. [latex]-120^circ[/latex]

23. [latex]-210^circ[/latex]

24. [latex]frac{5pi }{4}[/latex]

25. [latex]frac{7pi }{6}[/latex]

26. [latex]frac{5pi }{3}[/latex]

27. [latex]frac{3pi }{4}[/latex]

28. [latex]frac{4pi }{3}[/latex]

29. [latex]frac{2pi }{3}[/latex]

30. [latex]frac{-19pi }{6}[/latex]

31. [latex]frac{-9pi }{4}[/latex]

For the following exercises, find the reference angle, the quadrant of the terminal side, and the exact value of the trigonometric function.

32. [latex]tan frac{5pi }{6}[/latex]

33. [latex]sec frac{7pi }{6}[/latex]

34. [latex]csc frac{11pi }{6}[/latex]

35. [latex]cot frac{13pi }{6}[/latex]

36. [latex]tan frac{15pi }{4}[/latex]

37. [latex]sec frac{3pi }{4}[/latex]

38. [latex]csc frac{5pi }{4}[/latex]

39. [latex]cot frac{11pi }{4}[/latex]

40. [latex]tan left(-frac{4pi }{3}right)[/latex]

41. [latex]sec left(-frac{2pi }{3}right)[/latex]

42. [latex]csc left(-frac{10pi }{3}right)[/latex]

43. [latex]cot left(-frac{7pi }{3}right)[/latex]

44. [latex]tan 225^circ[/latex]

45. [latex]sec 300^circ[/latex]

46. [latex]csc 510^circ[/latex]

47. [latex]cot 600^circ[/latex]

48. [latex]tan left(-30^circright)[/latex]

49. [latex]sec left(-210^circright)[/latex]

50. [latex]csc left(-510^circright)[/latex]

51. [latex]cot left(-405^circright)[/latex]

In the following exercises, use a right triangle to find the exact value.

52. If [latex]text{sin}t=frac{3}{4}[/latex], and [latex]t[/latex] is in quadrant II, find [latex]cos t,sec t,csc t,tan t,cot t[/latex].

53. If [latex]text{cos}t=-frac{1}{3}[/latex], and [latex]t[/latex] is in quadrant III, find [latex]sin t,sec t,csc t,tan t,cot t[/latex].

54. If [latex]tan t=frac{12}{5}[/latex], and [latex]0le t<frac{pi }{2}[/latex], find [latex]sin t,cos t,sec t,csc t[/latex], and [latex]cot t[/latex]. 55. If [latex]sin t=frac{sqrt{3}}{2}[/latex] and [latex]cos t=frac{1}{2}[/latex], find [latex]sec t,csc t,tan t[/latex], and [latex]cot t[/latex]. For the following exercises, find the exact value using reference angles. 56. [latex]sinleft(frac{11pi}{3}right)cosleft(frac{-5pi}{6}right)[/latex] 57. [latex]sinleft(frac{3pi}{4}right)cosleft(frac{5pi}{3}right)[/latex] 58. [latex]sinleft(frac{-4pi}{3}right)cosleft(frac{pi}{2}right)[/latex] 59. [latex]sinleft(frac{-9pi}{4}right)cosleft(frac{-pi}{6}right)[/latex] 60. [latex]sinleft(frac{pi}{6}right)cosleft(frac{-pi}{3}right)[/latex] 61. [latex]sinleft(frac{7pi}{4}right)cosleft(frac{-2pi}{3}right)[/latex] 62. [latex]cosleft(frac{5pi}{6}right)cosleft(frac{2pi}{3}right)[/latex] 63. [latex]cosleft(frac{-pi}{3}right)cosleft(frac{pi}{4}right)[/latex] 64. [latex]sinleft(frac{-5pi}{4}right)sinleft(frac{11pi}{6}right)[/latex] 65. [latex]sinleft(piright)sinleft(frac{pi}{6}right)