What Is The Square Root of 3? Value, Calculation, and FAQs

The square root of 3, approximately 1.732, is a real number that, when multiplied by itself, equals 3; explore its significance and methods of calculation at WHAT.EDU.VN. We provide fast and free answers to your questions, bridging knowledge gaps effortlessly. Discover its applications and related concepts like irrational numbers, radical expressions, and long division methods.

1. Understanding the Square Root of 3

The square root of 3, denoted as √3, is a fundamental concept in mathematics. It represents the positive real number that, when multiplied by itself, equals 3. Understanding the square root of 3 involves recognizing its properties, calculation methods, and significance in various mathematical contexts.

1.1. Definition and Representation

The square root of 3 is an irrational number, meaning it cannot be expressed as a simple fraction. Its decimal representation is non-terminating and non-repeating. The value of √3 is approximately 1.732, and it is an algebraic number.

1.2. Why is √3 Important?

• Geometry: It appears in geometric calculations, such as the height of an equilateral triangle.
• Trigonometry: It is used in trigonometric ratios like tan(60°) and cot(30°).
• Calculus: It is found in various calculus problems, especially those involving integrals and derivatives.
• Engineering and Physics: It is relevant in fields such as electrical engineering (AC circuit analysis) and physics (mechanics and wave phenomena).

2. Methods to Calculate the Square Root of 3

Calculating the square root of 3 can be done using various methods, including the long division method, approximation techniques, and calculators. Each method offers a different approach to finding the value of √3.

2.1. Long Division Method

The long division method is a manual technique for finding the square root of a number. Here’s how it works for √3:

1. Start with 3.00 00 00: Pair the digits from right to left.
2. Find the largest integer whose square is less than or equal to 3: That’s 1 (1² = 1).
3. Divide and subtract: 3 ÷ 1 = 1 (quotient). Subtract 1² from 3, leaving 2.
4. Bring down the next pair of zeros: This gives you 200.
5. Double the quotient (1) to get 2: Find a digit ‘x’ such that 2x x is less than or equal to 200. ‘x’ is 7 (27 7 = 189).
6. Repeat: Subtract 189 from 200, leaving 11. Bring down the next pair of zeros, getting 1100.
7. Continue the process: Double the current quotient (17) to get 34. Find a digit ‘y’ such that 34y y is less than or equal to 1100. ‘y’ is 3 (343 3 = 1029).
8. Iterate: This process can be continued to get more decimal places.

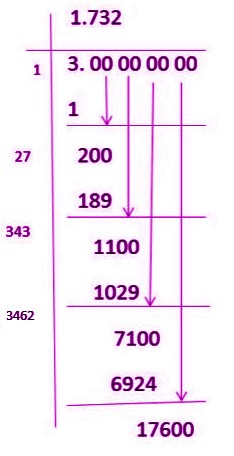Long division method for finding square root of 3

2.2. Approximation Method

Approximation methods involve estimating the value of √3 using iterative techniques. One such method is the Babylonian method:

1. Start with an initial guess: For example, let’s start with x = 2.
2. Iterate using the formula: x_next = 0.5 * (x + 3/x).
3. Repeat until convergence:
   • x_next = 0.5 * (2 + 3/2) = 1.75
   • x_next = 0.5 * (1.75 + 3/1.75) ≈ 1.732
4. Stop when the value stabilizes: After a few iterations, the value converges to approximately 1.732.

2.3. Using Calculators and Software

Calculators and software tools provide a quick and accurate way to find the square root of 3. Most scientific calculators have a square root function (√), which directly computes the value. Similarly, software like MATLAB, Python (with libraries like NumPy), and online calculators can be used.

Example using Python:

import numpy as np
result = np.sqrt(3)
print(result)  # Output: 1.7320508075688772

3. Applications of the Square Root of 3

The square root of 3 has numerous applications across various fields, including mathematics, physics, engineering, and computer science. Understanding these applications highlights its practical significance.

3.1. Mathematical Applications

• Geometry:
  • Equilateral Triangles: The height of an equilateral triangle with side length a is (√3/2)a.
  • 30-60-90 Triangles: In a 30-60-90 triangle, the ratio of the sides opposite the 60° angle to the side opposite the 30° angle is √3.
• Trigonometry:
  • tan(60°) = √3
  • cot(30°) = √3

3.2. Physics Applications

• Mechanics: In analyzing forces and vectors, especially in 2D and 3D space, √3 often appears when dealing with angles of 30°, 60°, or 90°.
• Wave Phenomena: In wave mechanics, particularly in the study of triangular waveforms and interference patterns.
• Electrical Engineering: In AC circuit analysis, especially when dealing with three-phase power systems.

3.3. Engineering Applications

• Structural Engineering: In calculating the stability and stress distribution in triangular structures.
• Acoustics: In designing acoustic panels and soundproofing materials, often involving triangular or hexagonal patterns.
• Robotics: In robot kinematics and dynamics, particularly in systems with triangular or hexagonal configurations.

3.4. Computer Science Applications

• Graphics and Game Development: In 3D graphics, √3 is used in calculations involving vectors, transformations, and rendering of triangular meshes.
• Data Analysis: In statistical analysis and data modeling, especially in techniques involving Euclidean distances and vector norms.
• Algorithm Design: In algorithms related to geometry and spatial data structures, such as Voronoi diagrams and Delaunay triangulations.

4. Properties of the Square Root of 3

Understanding the properties of the square root of 3 is crucial for advanced mathematical calculations and applications. These properties include its irrationality, algebraic nature, and decimal approximation.

4.1. Irrationality

The square root of 3 is an irrational number, which means it cannot be expressed as a fraction p/q, where p and q are integers. This can be proven using proof by contradiction.

Proof:

1. Assume √3 is rational, so √3 = p/q, where p and q are coprime integers (no common factors other than 1).
2. Square both sides: 3 = p²/q².
3. Rearrange: p² = 3q².
4. This implies p² is divisible by 3, and therefore p is also divisible by 3 (since 3 is prime).
5. Let p = 3k for some integer k.
6. Substitute into the equation: (3k)² = 3q² => 9k² = 3q² => 3k² = q².
7. This implies q² is divisible by 3, and therefore q is also divisible by 3.
8. Contradiction: Both p and q are divisible by 3, which contradicts the initial assumption that p and q are coprime.
9. Conclusion: √3 is irrational.

4.2. Algebraic Number

The square root of 3 is an algebraic number because it is a root of the polynomial equation x² – 3 = 0. Algebraic numbers are numbers that can be a root of a non-zero polynomial equation with integer coefficients.

4.3. Decimal Approximation

The decimal approximation of √3 is approximately 1.732. This approximation is commonly used in practical calculations where an exact value is not necessary. The approximation can be extended to more decimal places for higher accuracy:

• √3 ≈ 1.7320508075688772

5. Advanced Concepts Related to Square Root of 3

Exploring advanced concepts related to the square root of 3 provides a deeper understanding of its role in mathematics and related fields. These concepts include radical expressions, complex numbers, and its occurrence in various theorems.

5.1. Radical Expressions

Radical expressions involve square roots and other roots of numbers. The square root of 3 is a simple radical expression, but it can appear in more complex forms:

• Simplifying Radicals: √12 = √(4 * 3) = 2√3
• Rationalizing Denominators: 1/√3 = √3/3
• Combining Radicals: 2√3 + 5√3 = 7√3

5.2. Complex Numbers

In the context of complex numbers, the square root of 3 can appear in expressions involving imaginary units:

• Complex Conjugates: If z = a + b√3, then its conjugate is z* = a – b√3.
• Magnitude of Complex Numbers: |z| = √(a² + 3b²), where z = a + b√3i.

5.3. Theorems and Proofs

The square root of 3 appears in various mathematical theorems and proofs:

• Pythagorean Theorem: In a right triangle with sides a, b, and c (where c is the hypotenuse), if a = 1 and b = √3, then c = √(1² + (√3)²) = 2.
• Euler’s Formula: e^(iπ/3) = cos(π/3) + i sin(π/3) = 0.5 + i(√3/2), where √3 appears in the imaginary part.

6. Practical Examples and Problem Solving

Understanding how to apply the square root of 3 in practical examples and problem-solving scenarios enhances its relevance and usefulness. These examples cover geometry, trigonometry, and calculus.

6.1. Geometry Problems

Problem: Find the area of an equilateral triangle with side length 4.

Solution:

1. Formula: Area = (√3/4) * a², where a is the side length.
2. Substitute: Area = (√3/4) 4² = (√3/4) 16 = 4√3.
3. Approximate: Area ≈ 4 * 1.732 ≈ 6.928 square units.

6.2. Trigonometry Problems

Problem: Evaluate tan(60°).

Solution:

1. Recall: tan(60°) = √3.
2. Approximate: tan(60°) ≈ 1.732.

Problem: Determine the height of a tree if the angle of elevation from a point 20 meters away from the base of the tree is 60°.

Solution:

1. Formula: Height = Distance * tan(Angle).
2. Substitute: Height = 20 tan(60°) = 20 √3.
3. Approximate: Height ≈ 20 * 1.732 ≈ 34.64 meters.

6.3. Calculus Problems

Problem: Evaluate the integral ∫(0 to 1) x * √(3 – x²) dx.

Solution:

1. Substitute: Let u = 3 – x², then du = -2x dx.
2. Rewrite the integral: ∫(3 to 2) -0.5 √u du = -0.5 [ (2/3) * u^(3/2) ] (from 3 to 2).
3. Evaluate: -0.5 [ (2/3) (2^(3/2) – 3^(3/2)) ] = -(1/3) * (2√2 – 3√3).
4. Simplify: (3√3 – 2√2) / 3.

7. The Square Root of 3 in Everyday Life

While the square root of 3 is often encountered in academic and technical contexts, it also has relevance in everyday life. Understanding these connections can make mathematical concepts more relatable.

7.1. Construction and Design

In construction and design, the square root of 3 is used in calculations involving triangular structures, such as roof trusses and geodesic domes. These structures provide stability and efficient use of materials.

7.2. Carpentry and DIY Projects

In carpentry, the square root of 3 is used when creating precise angles and cuts, particularly in projects involving equilateral triangles or hexagonal shapes.

7.3. Art and Aesthetics

Artists and designers sometimes use geometric ratios involving the square root of 3 to create visually appealing compositions. These ratios can be found in patterns, mosaics, and other artistic creations.

8. Tips and Tricks for Remembering the Value of √3

Remembering the value of the square root of 3 can be helpful for quick calculations and estimations. Here are some tips and tricks to help you memorize it:

8.1. Mnemonic Devices

Create a mnemonic device or memorable phrase that helps you recall the digits of √3. For example:

• “I ate three too” (1.732)

8.2. Association with Geometric Shapes

Associate the square root of 3 with geometric shapes like equilateral triangles or 30-60-90 triangles. Visualizing these shapes can help you remember its value.

8.3. Repetition and Practice

Regularly use the value of √3 in calculations and problem-solving exercises. Repetition will reinforce your memory and make it easier to recall.

9. Common Mistakes and How to Avoid Them

When working with the square root of 3, it’s important to be aware of common mistakes and how to avoid them. These mistakes can occur in calculations, approximations, and applications.

9.1. Calculation Errors

• Mistake: Incorrectly calculating the square root using manual methods or calculators.
• Solution: Double-check your calculations and use reliable tools to verify your results.

9.2. Approximation Errors

• Mistake: Using an inaccurate approximation of √3, leading to significant errors in calculations.
• Solution: Use a sufficient number of decimal places (e.g., 1.732) or use the exact value in intermediate steps.

9.3. Application Errors

• Mistake: Misapplying the square root of 3 in geometric or trigonometric problems.
• Solution: Understand the underlying principles and formulas, and carefully consider the context of the problem.

10. Frequently Asked Questions (FAQs) about the Square Root of 3

Here are some frequently asked questions about the square root of 3, along with detailed answers:

Q1: What is the value of the square root of 3?

The square root of 3 (√3) is approximately 1.732. It is an irrational number, meaning its decimal representation is non-terminating and non-repeating. Knowing this value is crucial for various calculations in mathematics, physics, and engineering.

Q2: How do you calculate the square root of 3 without a calculator?

You can calculate the square root of 3 using the long division method or approximation techniques like the Babylonian method. The long division method involves a step-by-step process of dividing and subtracting to find the square root, while the Babylonian method uses an iterative formula to refine an initial guess.

Q3: Why is the square root of 3 important in trigonometry?

The square root of 3 is essential in trigonometry because it appears in the trigonometric ratios of certain angles, such as 30°, 60°, and 90°. For example, tan(60°) = √3 and cot(30°) = √3. These ratios are fundamental in solving trigonometric problems and understanding geometric relationships.

Q4: Is the square root of 3 a rational or irrational number?

The square root of 3 is an irrational number. This means it cannot be expressed as a simple fraction p/q, where p and q are integers. Its decimal representation is non-terminating and non-repeating, which is characteristic of irrational numbers.

Q5: What are some real-world applications of the square root of 3?

The square root of 3 has many real-world applications in fields such as:

• Construction: Calculating dimensions and stability in triangular structures.
• Engineering: Analyzing forces and vectors in mechanics.
• Computer Graphics: Rendering 3D models and calculating transformations.
• Physics: Studying wave phenomena and electrical circuits.

Q6: How can I remember the value of the square root of 3?

You can use mnemonic devices or associate it with geometric shapes to remember the value of the square root of 3. For example, you can use the phrase “I ate three too” (1.732) or visualize an equilateral triangle.

Q7: What is the square root of 3 used for in geometry?

In geometry, the square root of 3 is used to calculate the height of an equilateral triangle, the area of an equilateral triangle, and the relationships between sides in 30-60-90 triangles. It is also used in various geometric constructions and proofs.

Q8: How does the square root of 3 relate to complex numbers?

In complex numbers, the square root of 3 can appear in expressions involving imaginary units. For example, complex conjugates and magnitudes of complex numbers may involve √3 in their calculations.

Q9: Can the square root of 3 be simplified further?

No, the square root of 3 cannot be simplified further in terms of elementary radicals. It is already in its simplest radical form.

Q10: What is the difference between the square root of 3 and the cube root of 3?

The square root of 3 (√3) is the number that, when multiplied by itself, equals 3. The cube root of 3 (∛3) is the number that, when multiplied by itself twice, equals 3. Their values are different: √3 ≈ 1.732 and ∛3 ≈ 1.442.

Do you have more questions about math or any other subject? Visit what.edu.vn to ask your questions and receive fast, accurate, and free answers from our community of experts. Our platform is designed to provide easy access to knowledge and help you overcome any learning challenges. Contact us at 888 Question City Plaza, Seattle, WA 98101, United States or via Whatsapp at +1 (206) 555-7890. We’re here to help you learn and grow!