The area of a triangle represents the total space enclosed within its three sides, a fundamental concept in geometry, and WHAT.EDU.VN provides a comprehensive exploration of how to calculate it. This guide will cover various methods, from the basic formula using base and height to more advanced techniques like Heron’s formula, ensuring you can confidently tackle any triangle-related problem with insights into area calculation, geometric shapes, and spatial reasoning. Eager to learn more? Let’s dive in and explore the fascinating world of triangles together on WHAT.EDU.VN.
1. Understanding the Basic Area of a Triangle Formula
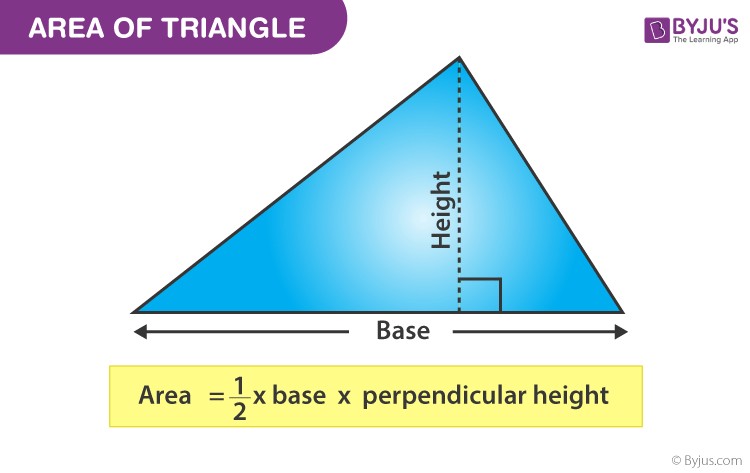
The most fundamental way to determine the area of a triangle involves using its base and height. This method applies universally to all triangles, irrespective of their shape or size.
-
The formula is expressed as: Area = 1/2 × base × height
-
Base (b): This refers to any side of the triangle chosen as the base.
-
Height (h): This is the perpendicular distance from the base to the opposite vertex (the highest point away from the base).
-
To effectively use this formula, you must ensure the height is measured perpendicularly to the base. This may sometimes require visualizing or drawing an additional line to represent the exact height.
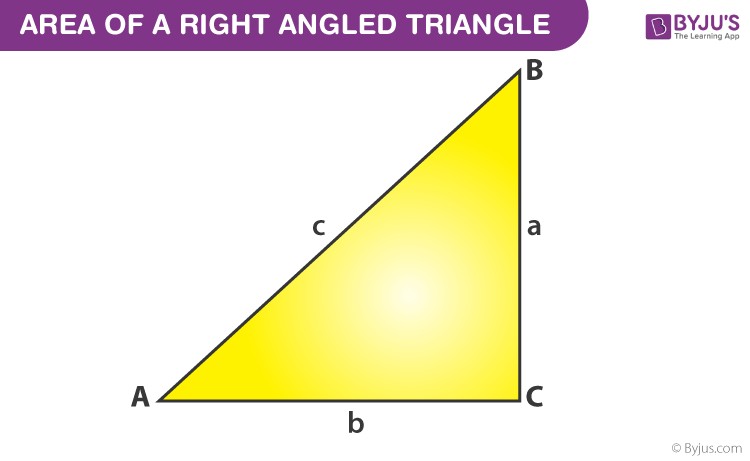
2. Calculating Area of a Right-Angled Triangle
A right-angled triangle simplifies the area calculation because one of its angles is exactly 90 degrees. In this type of triangle, the height and base are conveniently the two sides that form the right angle.
- Area of a Right Triangle = 1/2 × Base × Height
In a right triangle, if you know the lengths of the two sides adjacent to the right angle, you can easily compute the area without needing to find the perpendicular height separately.
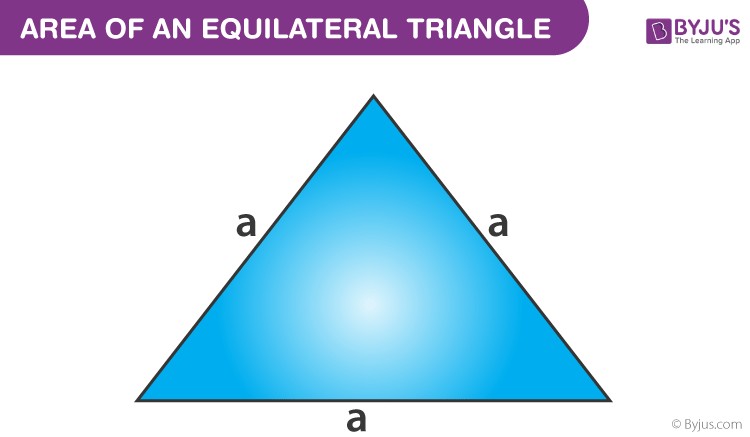
3. Finding the Area of an Equilateral Triangle
An equilateral triangle has three equal sides and three equal angles (each 60 degrees). Calculating its area requires a specific formula that takes into account the symmetry of the shape.
-
The formula to calculate the area of an equilateral triangle is:
-
Area = (√3 / 4) × side²
-
Where “side” is the length of any of the triangle’s sides.
-
This formula is derived using the Pythagorean theorem and properties of 30-60-90 special right triangles, making it a straightforward calculation if you know the length of one side.
4. Determining the Area of an Isosceles Triangle
An isosceles triangle features two sides of equal length. Calculating its area requires either knowing the height or using a modified formula if only the side lengths are known.
-
If you know the base (b) and the height (h):
- Area = 1/2 × b × h
-
If you know the length of the equal sides (a) and the base (b):
- Area = (b / 4) × √(4a² – b²)
This formula is derived by splitting the isosceles triangle into two right-angled triangles and applying the Pythagorean theorem.
5. Area of a Triangle with Three Sides (Heron’s Formula)
When all three sides of a triangle are known, but the height is not readily available, Heron’s formula provides a method to calculate the area using only the side lengths.
-
Heron’s formula is:
-
Area = √[s(s – a)(s – b)(s – c)]
-
Where a, b, and c are the lengths of the sides of the triangle,
-
s is the semi-perimeter of the triangle, calculated as s = (a + b + c) / 2
-
-
Heron’s formula is particularly useful for scalene triangles where the sides are of different lengths, and finding the height would require additional calculations.
6. Calculating Area Using Two Sides and an Included Angle (SAS)
When you know two sides of a triangle and the angle between them (Side-Angle-Side or SAS), you can use trigonometric functions to find the area.
-
The formula using trigonometry is:
-
Area = 1/2 × a × b × sin(C)
-
Where a and b are the lengths of the two sides,
-
C is the angle included between these sides.
-
-
This method is invaluable in scenarios where direct measurements of height are impractical, but angles and side lengths are known.
7. Practical Examples of Calculating Triangle Areas
To solidify your understanding, let’s walk through a few examples applying the different formulas discussed.
-
Example 1: Using Base and Height
-
Problem: Find the area of a triangle with a base of 10 cm and a height of 7 cm.
-
Solution: Area = 1/2 × base × height = 1/2 × 10 cm × 7 cm = 35 cm²
-
-
Example 2: Right-Angled Triangle
-
Problem: Calculate the area of a right triangle with sides 5 cm and 12 cm forming the right angle.
-
Solution: Area = 1/2 × 5 cm × 12 cm = 30 cm²
-
-
Example 3: Equilateral Triangle
-
Problem: Determine the area of an equilateral triangle with sides of 6 cm.
-
Solution: Area = (√3 / 4) × 6² = (√3 / 4) × 36 = 9√3 cm² ≈ 15.59 cm²
-
-
Example 4: Using Heron’s Formula
-
Problem: A triangle has sides of 4 cm, 13 cm, and 15 cm. Find its area.
-
Solution: First, calculate the semi-perimeter s = (4 + 13 + 15) / 2 = 16 cm. Then, use Heron’s formula:
- Area = √[16(16 – 4)(16 – 13)(16 – 15)] = √(16 × 12 × 3 × 1) = √576 = 24 cm²
-
-
Example 5: Using Two Sides and an Included Angle
-
Problem: Find the area of a triangle where two sides are 8 cm and 5 cm, and the included angle is 60 degrees.
-
Solution: Area = 1/2 × 8 cm × 5 cm × sin(60°) = 1/2 × 40 cm² × (√3 / 2) = 10√3 cm² ≈ 17.32 cm²
-
8. Common Mistakes and How to Avoid Them
Calculating the area of a triangle might seem straightforward, but certain common mistakes can lead to incorrect results. Here’s how to avoid them:
-
Incorrectly Identifying the Height:
-
Mistake: Using a side that is not perpendicular to the base as the height.
-
Solution: Always ensure that the height is measured perpendicularly from the base to the opposite vertex. If necessary, draw a line to represent the true height.
-
-
Misapplying Heron’s Formula:
-
Mistake: Forgetting to calculate the semi-perimeter correctly or misusing the formula.
-
Solution: Double-check the semi-perimeter calculation (s = (a + b + c) / 2) and ensure all side lengths are correctly substituted into Heron’s formula: Area = √[s(s – a)(s – b)(s – c)].
-
-
Using the Wrong Units:
-
Mistake: Mixing units (e.g., using meters for base and centimeters for height).
-
Solution: Ensure all measurements are in the same units before calculating the area. Convert if necessary, and remember to express the area in square units (e.g., cm², m²).
-
-
Confusing Formulas for Different Triangles:
-
Mistake: Applying the equilateral triangle formula to an isosceles or scalene triangle.
-
Solution: Understand the specific conditions for each formula. The equilateral triangle formula applies only to equilateral triangles, while Heron’s formula is versatile for any triangle when all three sides are known.
-
-
Errors in Trigonometric Calculations:
-
Mistake: Incorrectly calculating the sine of an angle or using the wrong angle in the area formula.
-
Solution: Ensure your calculator is in the correct mode (degrees or radians) and double-check the angle measurement. The correct formula is Area = 1/2 × a × b × sin(C), where C is the angle between sides a and b.
-
-
Rounding Errors:
-
Mistake: Rounding intermediate calculations too early, leading to a significant final error.
-
Solution: Keep as many decimal places as possible during intermediate calculations and only round the final answer to the required precision.
-
-
Not Visualizing the Problem:
-
Mistake: Trying to apply formulas without understanding the triangle’s properties or dimensions.
-
Solution: Draw a diagram of the triangle and label all known values. This visual aid can help prevent errors in identifying the correct base, height, or angles.
-
By being mindful of these common pitfalls and following the suggested solutions, you can increase your accuracy and confidence in calculating the area of a triangle in various contexts.
9. Advanced Applications of Triangle Area
Understanding the area of a triangle extends beyond basic geometry and has significant applications in various fields, including engineering, surveying, and computer graphics.
-
Engineering:
-
Structural Design: Engineers use triangle area calculations to determine the strength and stability of structures. Triangles are fundamental in trusses and frameworks, and their area helps calculate load distribution and stress.
-
Fluid Dynamics: In designing aircraft wings or ship hulls, the area of triangular sections is crucial for calculating lift, drag, and overall aerodynamic or hydrodynamic performance.
-
-
Surveying:
-
Land Measurement: Surveyors use triangulation techniques to measure land areas. By dividing a plot of land into triangles, they can accurately calculate the area using side lengths and angles. This is particularly useful for irregular shapes where direct measurement is difficult.
-
Mapping: Triangle area calculations are essential in creating accurate maps, especially in mountainous regions where terrain is uneven.
-
-
Computer Graphics:
-
3D Modeling: Triangles are the basic building blocks of 3D models. The efficiency and realism of these models depend on accurate area calculations for rendering and shading.
-
Game Development: In video games, triangle area calculations are used for collision detection, determining the size of textures, and creating realistic environments.
-
-
Navigation:
-
Piloting: Pilots use triangle area calculations for route planning and determining distances, especially in situations where direct radar or GPS data is unavailable.
-
Sailing: Sailors use similar techniques to calculate sail area, which is essential for optimizing sail performance under different wind conditions.
-
-
Architecture:
-
Roofing: Architects use triangle area calculations to determine the amount of roofing material needed for triangular roof sections.
-
Aesthetic Design: Triangles are often used in modern architectural designs for aesthetic appeal. Calculating their area helps in planning material usage and ensuring structural integrity.
-
-
Physics:
-
Mechanics: Calculating the area of triangles is important in physics for determining the center of mass and moment of inertia of triangular objects.
-
Optics: In optics, triangle area calculations are used in designing prisms and lenses to calculate refraction and dispersion of light.
-
-
Real Estate and Urban Planning:
-
Property Assessment: Calculating the area of triangular plots helps in property assessment and taxation.
-
Park Design: Urban planners use triangle area calculations to design parks and recreational areas, optimizing space utilization and creating aesthetically pleasing layouts.
-
These diverse applications highlight the importance of understanding how to accurately calculate the area of a triangle. Whether in professional fields or everyday problem-solving, a solid grasp of these principles is invaluable.
10. Area of a Triangle: FAQs Answered
To further clarify the concept, here are some frequently asked questions about the area of a triangle:
| Question | Answer |
|---|---|
| What is the basic formula for the area of a triangle? | The basic formula is Area = 1/2 × base × height, where the height is the perpendicular distance from the base to the opposite vertex. |
| How do I find the area if I only know the three sides? | You can use Heron’s formula: Area = √[s(s – a)(s – b)(s – c)], where a, b, and c are the lengths of the sides, and s is the semi-perimeter of the triangle, calculated as s = (a + b + c) / 2. |
| What if the triangle is a right triangle? | For a right triangle, the area is 1/2 × base × height, where the base and height are the two sides that form the right angle. |
| How do I calculate the area of an equilateral triangle? | The formula for an equilateral triangle is Area = (√3 / 4) × side², where side is the length of any of the triangle’s sides. |
| Can I find the area if I know two sides and an angle? | Yes, if you know two sides (a and b) and the included angle (C), use the formula: Area = 1/2 × a × b × sin(C). |
| What is the unit of measurement for the area? | The area is measured in square units. If the sides are in centimeters, the area will be in square centimeters (cm²); if in meters, the area will be in square meters (m²), and so on. |
| How accurate do I need to be in my measurements? | The accuracy of your area calculation depends on the accuracy of your measurements. For practical purposes, measure to the nearest reasonable unit. In precise calculations, use as many decimal places as possible and round only the final answer. |
| What is the semi-perimeter in Heron’s formula? | The semi-perimeter (s) is half the sum of the lengths of all three sides of the triangle. It is calculated as s = (a + b + c) / 2. |
| Why is the height perpendicular to the base? | The height must be perpendicular to the base to accurately measure the vertical extent of the triangle from the base to the highest point (vertex). This ensures that the area calculation reflects the true two-dimensional space enclosed by the triangle. |
| Can I use any side as the base of a triangle? | Yes, any side of the triangle can be chosen as the base. However, the height must be measured perpendicularly from the chosen base to the opposite vertex. The area will be the same regardless of which side you choose as the base, provided you use the corresponding height. |
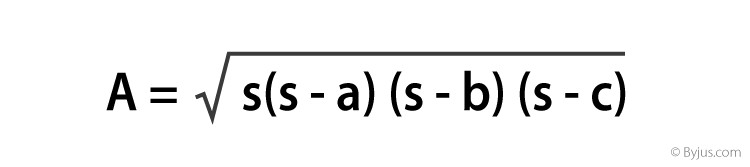
These FAQs should address common queries and provide a clearer understanding of how to approach different scenarios when calculating the area of a triangle.
Navigating the world of geometry can sometimes feel like a complex maze, but understanding the area of a triangle doesn’t have to be daunting. Whether you’re a student tackling homework, a professional working on a project, or simply a curious mind eager to learn, mastering this fundamental concept opens doors to countless applications.
At WHAT.EDU.VN, we understand the challenges of finding clear, reliable answers to your questions. That’s why we’re dedicated to providing you with comprehensive guides and expert insights, all in one convenient place.
Do you have more burning questions about triangles, geometry, or any other topic under the sun? Don’t let your curiosity wait! Visit WHAT.EDU.VN today and ask your question for free. Our community of experts is ready to provide you with accurate, easy-to-understand answers, helping you unlock your full learning potential.
Ready to take the next step in your learning journey? Head over to WHAT.EDU.VN now and ask your question for free!
Contact us:
- Address: 888 Question City Plaza, Seattle, WA 98101, United States
- WhatsApp: +1 (206) 555-7890
- Website: WHAT.EDU.VN
Join us at what.edu.vn, where asking questions is not just encouraged—it’s celebrated. Let’s explore the world together, one question at a time!