Avogadro’s number is 6.02214076 × 10^23, representing the number of atoms or molecules in a mole, crucial for stoichiometric calculations; and at WHAT.EDU.VN, we can help you understand how this constant impacts chemistry and other scientific fields. This constant helps link the macroscopic world (grams) to the atomic world (atomic mass units) and is vital for quantitative chemical analysis, molar mass calculations, and understanding gas laws. For a deeper understanding of molar volume, atomic weights, and standard atomic weight, ask your questions at WHAT.EDU.VN for free and get professional answers.
1. Understanding Avogadro’s Number: The Foundation of Chemical Calculations
1.1 What is Avogadro’s Number and How Was It Determined?
Avogadro’s number, approximately 6.022 x 10^23, is the number of atoms, molecules, or other specified entities in one mole of a substance. Initially, Avogadro did not determine this number; rather, his hypothesis (Avogadro’s Law) stated that equal volumes of all gases, at the same temperature and pressure, contain the same number of molecules. This constant was later named in his honor because of his foundational work. The actual determination of Avogadro’s number has been achieved through various experimental methods.
1.2 Methods for Determining Avogadro’s Number
Several methods have been employed to accurately measure Avogadro’s number:
- Electrolysis: Electrolysis of water, measuring the volume of hydrogen and oxygen produced from a known quantity of electricity.
- Brownian Motion: Observing Brownian motion of particles suspended in a liquid and applying statistical mechanics.
- X-ray Diffraction: Using X-ray diffraction to measure the volume of the unit cell in a crystal and relating it to the molar volume.
1.3 Why is Avogadro’s Number Important in Chemistry?
Avogadro’s number serves as a bridge between the macroscopic world (grams) and the microscopic world (atomic mass units). It allows chemists to:
- Convert between mass and moles: Essential for stoichiometric calculations in chemical reactions.
- Determine molar masses: Calculating the mass of one mole of a compound based on its chemical formula.
- Calculate gas volumes: Applying the ideal gas law and other gas laws in quantitative analysis.
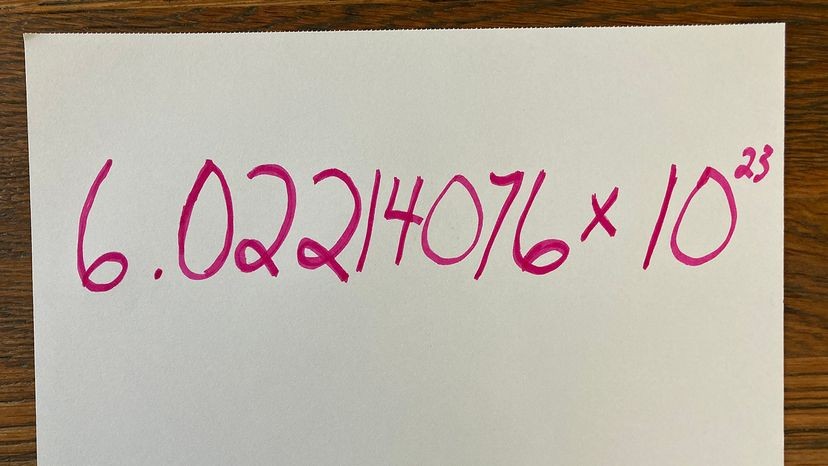Avogadro's Number and Moles
1.4 Avogadro’s Hypothesis vs. Avogadro’s Law
Avogadro’s Hypothesis, now known as Avogadro’s Law, states that equal volumes of all gases at the same temperature and pressure contain the same number of molecules. This principle is crucial in understanding the behavior of gases and forms the basis for gas stoichiometry.
2. The Mole Concept: Linking Microscopic and Macroscopic Worlds
2.1 What is a Mole?
A mole is a unit of measurement that represents 6.022 x 10^23 entities (atoms, molecules, ions, etc.). It’s similar to how “dozen” represents 12 items. The mole concept is central to quantitative chemistry, allowing chemists to work with measurable quantities of substances.
2.2 How is the Mole Related to Avogadro’s Number?
One mole contains Avogadro’s number of entities. Therefore, the mole is directly linked to Avogadro’s number, providing a practical way to count atoms and molecules by measuring mass.
2.3 Practical Examples of Using the Mole in Chemistry
Consider the reaction:
2H2 + O2 → 2H2O
This equation tells us that 2 moles of hydrogen react with 1 mole of oxygen to produce 2 moles of water. Using molar masses, we can calculate the mass of each substance involved:
- 2 moles of H2 = 2 x 2.016 g = 4.032 g
- 1 mole of O2 = 1 x 32.00 g = 32.00 g
- 2 moles of H2O = 2 x 18.02 g = 36.04 g
2.4 How Does the Mole Concept Simplify Chemical Calculations?
The mole concept simplifies chemical calculations by:
- Providing a standard unit: Allows easy conversion between mass, moles, and number of particles.
- Balancing chemical equations: Ensures accurate stoichiometric relationships in reactions.
- Determining limiting reactants: Helps identify the reactant that limits the amount of product formed.
3. Applications of Avogadro’s Number in Stoichiometry
3.1 What is Stoichiometry?
Stoichiometry is the branch of chemistry that deals with the quantitative relationships between reactants and products in chemical reactions. It relies heavily on the mole concept and Avogadro’s number to ensure accurate calculations.
3.2 How Avogadro’s Number is Used in Stoichiometric Calculations
Avogadro’s number is used in stoichiometric calculations to:
- Convert grams to moles: Determining the number of moles in a given mass of a substance.
- Convert moles to grams: Calculating the mass of a specified number of moles of a substance.
- Determine mole ratios: Establishing the ratios of reactants and products in a balanced chemical equation.
3.3 Example Stoichiometric Problem and Solution
Problem: How many grams of oxygen are required to completely react with 10 grams of methane (CH4) in the following reaction?
CH4 + 2O2 → CO2 + 2H2O
Solution:
- Convert grams of CH4 to moles:
Molar mass of CH4 = 12.01 (C) + 4 x 1.008 (H) = 16.04 g/mol
Moles of CH4 = 10 g / 16.04 g/mol = 0.623 moles - Determine mole ratio of O2 to CH4:
From the balanced equation, 1 mole of CH4 reacts with 2 moles of O2.
Moles of O2 required = 0.623 moles CH4 x (2 moles O2 / 1 mole CH4) = 1.246 moles - Convert moles of O2 to grams:
Molar mass of O2 = 2 x 16.00 g/mol = 32.00 g/mol
Grams of O2 required = 1.246 moles x 32.00 g/mol = 39.87 g
Therefore, 39.87 grams of oxygen are required to completely react with 10 grams of methane.
3.4 Common Mistakes in Stoichiometric Calculations and How to Avoid Them
Common mistakes in stoichiometric calculations include:
- Incorrectly balancing chemical equations: Always double-check the balanced equation before proceeding.
- Using incorrect molar masses: Verify the molar masses of all substances involved.
- Failing to convert units: Ensure all quantities are in the appropriate units (grams, moles, etc.).
- Ignoring mole ratios: Always use the correct mole ratios from the balanced equation.
4. Avogadro’s Number and the Ideal Gas Law
4.1 What is the Ideal Gas Law?
The Ideal Gas Law describes the relationship between pressure (P), volume (V), number of moles (n), ideal gas constant (R), and temperature (T) for an ideal gas:
PV = nRT
Where:
- P is the pressure of the gas
- V is the volume of the gas
- n is the number of moles of the gas
- R is the ideal gas constant (0.0821 L atm / (mol K) or 8.314 J / (mol K))
- T is the temperature of the gas in Kelvin
4.2 How Avogadro’s Number Relates to the Ideal Gas Law
Avogadro’s number is essential in the Ideal Gas Law because it relates the number of moles (n) to the number of molecules:
n = N / NA
Where:
- N is the number of molecules
- NA is Avogadro’s number
4.3 Using Avogadro’s Number and the Ideal Gas Law in Calculations
Problem: What volume is occupied by 2 moles of an ideal gas at standard temperature and pressure (STP)?
Solution:
At STP:
- P = 1 atm
- T = 273.15 K
- n = 2 moles
- R = 0.0821 L atm / (mol K)
Using the Ideal Gas Law:
V = (nRT) / P
V = (2 moles x 0.0821 L atm / (mol K) x 273.15 K) / 1 atm
V = 44.8 L
4.4 Limitations of the Ideal Gas Law and When to Use Real Gas Equations
The Ideal Gas Law assumes that gas particles have no volume and do not interact with each other. These assumptions are not valid at high pressures and low temperatures. In such cases, real gas equations, such as the Van der Waals equation, provide more accurate results:
(P + a(n/V)^2) (V – nb) = nRT
Where a and b are constants that account for intermolecular forces and the volume of gas particles, respectively.
5. Avogadro’s Number in Different Fields of Science
5.1 Applications in Nanotechnology
In nanotechnology, Avogadro’s number is used to calculate the number of atoms or molecules in nanoparticles, which is essential for controlling their properties and behavior.
5.2 Applications in Material Science
Material scientists use Avogadro’s number to determine the composition and structure of materials at the atomic level, aiding in the design of new materials with specific properties.
5.3 Applications in Environmental Science
Environmental scientists use Avogadro’s number to quantify pollutants and contaminants in air, water, and soil, ensuring accurate assessment and management of environmental risks.
5.4 Applications in Pharmaceutical Science
In pharmaceutical science, Avogadro’s number is crucial for determining the dosage of drugs and understanding their interactions with biological systems at the molecular level.
6. The Historical Context of Avogadro’s Number
6.1 Amedeo Avogadro’s Contributions to Chemistry
Amedeo Avogadro (1776-1856) was an Italian scientist who made significant contributions to the field of chemistry. His hypothesis, now known as Avogadro’s Law, laid the foundation for understanding the relationship between the number of particles and the volume of gases.
6.2 The Evolution of Determining Avogadro’s Number
The determination of Avogadro’s number has evolved through various experimental methods over the years, each providing more accurate and precise values. Key milestones include:
- Early 19th century: Initial estimations based on gas densities and electrochemical measurements.
- Late 19th century: Refinement using kinetic theory of gases and solution properties.
- Early 20th century: Precise measurements using Brownian motion and X-ray diffraction.
- Modern era: Highly accurate determinations using advanced techniques, such as single-crystal X-ray diffraction and the Kibble balance.
6.3 The Impact of Avogadro’s Work on Modern Chemistry
Avogadro’s work has had a profound impact on modern chemistry, providing the basis for:
- Stoichiometry: Accurate quantitative analysis of chemical reactions.
- Molar mass determination: Calculation of molecular weights and formula weights.
- Ideal gas law: Understanding the behavior of gases under various conditions.
- Molecular theory: Developing and refining models of molecular structure and behavior.
7. Understanding Molar Mass and Its Relationship to Avogadro’s Number
7.1 What is Molar Mass?
Molar mass is the mass of one mole of a substance, expressed in grams per mole (g/mol). It is numerically equal to the atomic or molecular weight of the substance in atomic mass units (amu).
7.2 How is Molar Mass Calculated?
Molar mass is calculated by summing the atomic masses of all the atoms in a molecule or formula unit. For example, the molar mass of water (H2O) is:
- 2 x Atomic mass of H (1.008 amu) = 2.016 g/mol
- 1 x Atomic mass of O (16.00 amu) = 16.00 g/mol
- Molar mass of H2O = 2.016 + 16.00 = 18.02 g/mol
7.3 The Relationship Between Molar Mass and Avogadro’s Number
Molar mass provides the link between the mass of a substance and the number of particles it contains. One mole of any substance has a mass equal to its molar mass, and it contains Avogadro’s number of particles.
7.4 Examples of Molar Mass Calculations for Different Compounds
- Sodium Chloride (NaCl):
Molar mass of Na = 22.99 g/mol
Molar mass of Cl = 35.45 g/mol
Molar mass of NaCl = 22.99 + 35.45 = 58.44 g/mol - Sulfuric Acid (H2SO4):
Molar mass of H = 1.008 g/mol
Molar mass of S = 32.07 g/mol
Molar mass of O = 16.00 g/mol
Molar mass of H2SO4 = (2 x 1.008) + 32.07 + (4 x 16.00) = 98.09 g/mol - Glucose (C6H12O6):
Molar mass of C = 12.01 g/mol
Molar mass of H = 1.008 g/mol
Molar mass of O = 16.00 g/mol
Molar mass of C6H12O6 = (6 x 12.01) + (12 x 1.008) + (6 x 16.00) = 180.16 g/mol
8. Practical Experiments to Demonstrate Avogadro’s Number
8.1 Simple Experiments for High School Students
- Determining the Volume of a Monolayer: Dissolve a known mass of stearic acid in a solvent, spread a drop on water, and calculate the area and thickness of the monolayer to estimate Avogadro’s number.
- Electrolysis of Water: Electrolyze water to produce hydrogen and oxygen gases, measuring the volumes produced to calculate the number of molecules and Avogadro’s number.
8.2 Advanced Experiments for University Students
- X-ray Diffraction: Use X-ray diffraction to determine the crystal structure of a compound and calculate the unit cell volume, relating it to the molar volume and Avogadro’s number.
- Kibble Balance: Employ a Kibble balance to measure the Planck constant and relate it to fundamental constants to determine Avogadro’s number with high precision.
8.3 Demonstrating the Scale of Avogadro’s Number with Everyday Objects
To illustrate the immense scale of Avogadro’s number:
- Grains of Sand: A mole of grains of sand would cover the entire surface of the Earth to a depth of several feet.
- Pennies: A mole of pennies would be enough to give every person on Earth trillions of dollars.
- Atoms in a Pinhead: A pinhead contains approximately 10^18 atoms, which is a tiny fraction of Avogadro’s number.
9. Common Misconceptions About Avogadro’s Number
9.1 Avogadro’s Number as a Fixed Quantity for All Substances
Avogadro’s number is a fixed quantity (6.022 x 10^23) that represents the number of entities in one mole of any substance, regardless of its chemical nature.
9.2 Confusing Molar Mass with Molecular Weight
Molar mass is the mass of one mole of a substance (g/mol), while molecular weight is the mass of one molecule in atomic mass units (amu). They are numerically equal but have different units and meanings.
9.3 Thinking Avogadro’s Number Only Applies to Gases
Avogadro’s number applies to all substances, whether they are gases, liquids, or solids. It provides the link between the macroscopic and microscopic worlds for any chemical species.
9.4 Overlooking the Importance of Units in Calculations
Always pay attention to units in calculations involving Avogadro’s number. Ensure that all quantities are expressed in consistent units (grams, moles, liters, etc.) to avoid errors.
10. Avogadro’s Number in Modern Research
10.1 Recent Advancements in Determining Avogadro’s Number
Recent advancements in determining Avogadro’s number include:
- Single-Crystal X-ray Diffraction: High-precision measurements of crystal structures to determine molar volume and Avogadro’s number.
- Kibble Balance: Using electromagnetic forces to measure mass and relate it to fundamental constants, providing highly accurate values for Avogadro’s number.
10.2 The Role of Avogadro’s Number in Quantum Computing
In quantum computing, Avogadro’s number is used to quantify the number of quantum particles or qubits needed for complex calculations and simulations.
10.3 How Avogadro’s Number Aids in Developing New Technologies
Avogadro’s number plays a crucial role in developing new technologies by:
- Nanomaterial Synthesis: Precisely controlling the number of atoms or molecules in nanomaterials to achieve desired properties.
- Drug Delivery Systems: Designing drug delivery systems that target specific cells or tissues based on molecular interactions.
- Energy Storage: Developing new materials for batteries and fuel cells with enhanced energy storage capabilities.
11. Avogadro’s Number and the Concept of Isotopes
11.1 What are Isotopes?
Isotopes are variants of a chemical element which have the same number of protons and electrons, but different numbers of neutrons, and consequently different nucleon numbers. All isotopes of a given element have the same atomic number but different mass numbers.
11.2 How Isotopes Affect Molar Mass Calculations
The presence of isotopes affects molar mass calculations because the atomic mass of an element is the weighted average of the masses of its isotopes. The atomic mass is calculated using the following formula:
Atomic Mass = (Abundance of Isotope 1 x Mass of Isotope 1) + (Abundance of Isotope 2 x Mass of Isotope 2) + …
11.3 Examples of Isotopic Abundance and Their Impact on Molar Mass
Consider chlorine (Cl), which has two stable isotopes:
- Chlorine-35 (35Cl) with an abundance of 75.77% and a mass of 34.96885 amu
- Chlorine-37 (37Cl) with an abundance of 24.23% and a mass of 36.96590 amu
The atomic mass of chlorine is calculated as:
Atomic Mass of Cl = (0.7577 x 34.96885) + (0.2423 x 36.96590) = 26.4959 + 8.9570 = 35.4529 amu
Therefore, the molar mass of chlorine is approximately 35.45 g/mol.
11.4 Using Isotopic Data to Refine Stoichiometric Calculations
In high-precision stoichiometric calculations, it is essential to consider the isotopic composition of elements. Using the exact isotopic masses and abundances can lead to more accurate results, especially when dealing with elements that have significant isotopic variations.
12. Teaching Avogadro’s Number: Tips and Strategies
12.1 Effective Ways to Introduce the Concept to Students
- Relate to Everyday Examples: Compare the mole to familiar units like “dozen” or “gross” to illustrate the concept of a fixed quantity.
- Use Visual Aids: Use diagrams, models, and animations to show the number of atoms or molecules in a mole.
- Hands-on Activities: Conduct experiments that allow students to measure quantities and convert them to moles.
12.2 Addressing Common Difficulties and Misconceptions
- Emphasize the Scale: Use analogies to help students grasp the immense size of Avogadro’s number.
- Clarify Units: Clearly explain the difference between molar mass and molecular weight.
- Practice Problems: Provide plenty of practice problems with step-by-step solutions.
12.3 Interactive Tools and Resources for Teaching Avogadro’s Number
- Online Simulations: Use interactive simulations to visualize molecular behavior and stoichiometric relationships.
- Virtual Labs: Conduct virtual labs that allow students to perform experiments and collect data.
- Educational Videos: Utilize educational videos to explain complex concepts in a simple and engaging manner.
12.4 Making Avogadro’s Number Relevant to Real-World Applications
Connect Avogadro’s number to real-world applications such as:
- Drug Dosage: Explain how molar mass and Avogadro’s number are used to determine the correct dosage of medications.
- Environmental Monitoring: Discuss how these concepts are used to measure and monitor pollutants in the environment.
- Materials Science: Describe how they are applied in the design and synthesis of new materials with specific properties.
13. The Future of Avogadro’s Number in Scientific Advancements
13.1 Potential New Applications in Emerging Fields
Avogadro’s number has the potential for new applications in emerging fields such as:
- Quantum Materials: Precisely controlling the composition and structure of quantum materials at the atomic level.
- Personalized Medicine: Developing personalized drug therapies based on individual genetic and metabolic profiles.
- Sustainable Energy: Designing new materials for energy storage and conversion with enhanced efficiency.
13.2 The Ongoing Quest for More Precise Measurements
Scientists are continuously striving for more precise measurements of Avogadro’s number using advanced techniques and technologies. These efforts aim to:
- Improve Accuracy: Reduce uncertainties in fundamental constants and measurements.
- Refine Models: Develop more accurate models of molecular behavior and interactions.
- Validate Theories: Test and validate fundamental theories in physics and chemistry.
13.3 How Avogadro’s Number Will Continue to Shape Scientific Understanding
Avogadro’s number will continue to shape scientific understanding by:
- Providing a Fundamental Link: Connecting the macroscopic and microscopic worlds.
- Enabling Quantitative Analysis: Facilitating precise quantitative analysis of chemical reactions and processes.
- Driving Innovation: Inspiring new discoveries and innovations in science and technology.
14. Frequently Asked Questions About Avogadro’s Number
14.1 What is the currently accepted value of Avogadro’s Number?
The currently accepted value of Avogadro’s number is 6.02214076 × 10^23 mol-1. This value was officially adopted in 2019 as part of the redefinition of the International System of Units (SI).
14.2 How does Avogadro’s Number relate to the mass of an atom?
Avogadro’s number relates the mass of an atom to the macroscopic unit of mass, the gram. Specifically, it connects the atomic mass unit (amu) to grams through the following relationship: 1 amu = 1 g / NA, where NA is Avogadro’s number.
14.3 Can Avogadro’s Number be used for substances other than elements and compounds?
Yes, Avogadro’s number can be used for any specified entity, including ions, electrons, and even hypothetical particles. It is a universal constant that defines the number of entities in one mole.
14.4 What are some real-world applications of Avogadro’s Number in industry?
Real-world applications of Avogadro’s number in industry include:
- Chemical Manufacturing: Ensuring precise control over reactant quantities in chemical processes.
- Pharmaceutical Production: Determining accurate dosages of drugs and medications.
- Materials Science: Synthesizing materials with specific compositions and properties.
- Environmental Monitoring: Quantifying pollutants and contaminants in environmental samples.
14.5 How is Avogadro’s Number used in determining the age of artifacts using carbon dating?
In carbon dating, Avogadro’s number is used to calculate the number of carbon-14 atoms in a sample and relate it to the decay rate. This information is then used to estimate the age of the artifact.
14.6 What is the difference between Avogadro’s Number and Loschmidt’s Number?
Avogadro’s number (NA) is the number of entities (atoms, molecules, etc.) per mole, while Loschmidt’s number (n0) is the number of gas particles per unit volume at standard temperature and pressure (STP). Loschmidt’s number can be derived from Avogadro’s number using the ideal gas law.
14.7 How does temperature affect the application of Avogadro’s Law?
Avogadro’s Law states that equal volumes of all gases, at the same temperature and pressure, contain the same number of molecules. Temperature and pressure must be kept constant for the law to hold true. Changes in temperature can affect the volume of gases, thus impacting the number of molecules per unit volume.
14.8 What role does Avogadro’s Number play in the development of nanotechnology?
In nanotechnology, Avogadro’s number is essential for calculating the number of atoms or molecules in nanoscale materials, which is critical for controlling their properties and behavior. It allows scientists to manipulate matter at the atomic and molecular levels.
14.9 How can I improve my understanding of Avogadro’s Number for chemistry exams?
To improve your understanding of Avogadro’s number for chemistry exams:
- Practice Problems: Solve a variety of stoichiometry and gas law problems.
- Review Concepts: Understand the definitions of mole, molar mass, and Avogadro’s Law.
- Use Visual Aids: Create diagrams and flowcharts to visualize the relationships between different concepts.
- Seek Help: Ask questions and seek help from teachers or tutors when you encounter difficulties.
14.10 Is Avogadro’s Number relevant in biochemistry or biology?
Yes, Avogadro’s number is relevant in biochemistry and biology. It is used in various applications, such as:
- Calculating Concentrations: Determining the molar concentrations of biological molecules in solutions.
- Enzyme Kinetics: Analyzing enzyme reactions and determining reaction rates.
- Macromolecule Studies: Investigating the structure and behavior of proteins, DNA, and other macromolecules.
Understanding Avogadro’s number is fundamental to grasping many concepts in chemistry and related sciences.
15. Conclusion: The Enduring Significance of Avogadro’s Number
Avogadro’s number is more than just a numerical constant; it is a cornerstone of modern chemistry, linking the microscopic world of atoms and molecules to the macroscopic world of measurable quantities. Its applications span across various scientific disciplines, from nanotechnology to environmental science, and its enduring significance lies in its ability to enable precise quantitative analysis and drive innovation. Whether you’re a student, a researcher, or simply a curious mind, understanding Avogadro’s number is essential for unraveling the mysteries of the chemical world. Explore further by researching molecular weight, molar volume, and the concept of relative atomic mass.
Still have questions about Avogadro’s number or any other scientific concept? Don’t hesitate to ask at WHAT.EDU.VN! Our platform provides free access to expert answers and resources to help you understand the world around you. Contact us at 888 Question City Plaza, Seattle, WA 98101, United States, Whatsapp: +1 (206) 555-7890, or visit our website at what.edu.vn. We’re here to help you discover the wonders of science!
