In mathematics, understanding different types of numbers is fundamental. Among these, rational numbers play a crucial role. A rational number is defined as any number that can be expressed in the form of a fraction p/q, where ‘p’ and ‘q’ are integers, and ‘q’ is not equal to zero. Essentially, if you can write a number as a simple fraction, it’s a rational number. Think of everyday fractions like 1/2, 3/4, or even seemingly complex ones – they all fall under the umbrella of rational numbers, provided the denominator isn’t zero.
Even the number zero itself is a rational number. We can represent zero as 0/1, 0/2, 0/3, and so on. However, it’s crucial to remember that division by zero is undefined in mathematics. Therefore, fractions like 1/0, 2/0, 3/0 are not rational numbers as they represent undefined or infinite values. To deepen your understanding and see how they contrast, you might also want to explore irrational numbers and their unique characteristics.
This article will comprehensively explore the concept of rational numbers. We’ll delve into their properties, different types, and how they differ from irrational numbers. We’ll also cover arithmetic operations involving rational numbers and provide examples to solidify your understanding. This guide is designed to give you a robust grasp of rational numbers and their significance in mathematics. We will also touch upon how to represent rational numbers on a number line, showcasing their position and order.
Let’s navigate through the world of rational numbers and uncover their intricacies.
Defining Rational Numbers in Detail
As we’ve touched upon, a rational number is any number expressible as a fraction p/q where both p and q are integers and q ≠ 0. This definition is the cornerstone of understanding rational numbers. Another way to think about it is through decimal representation. When a rational number, expressed as a fraction, is converted into a decimal, the result is either a terminating decimal (it ends after a finite number of digits) or a repeating decimal (a pattern of digits repeats indefinitely).
Identifying Rational Numbers: Key Criteria
To confidently identify whether a number is rational, consider these key conditions:
- Fraction Form: Can the number be written in the form p/q, where p and q are integers, and q is not zero? If yes, it’s rational.
- Decimal Representation: Does the decimal representation of the number terminate or repeat? If yes, it’s rational.
The set of rational numbers encompasses a wide range of numbers, including:
- Integers: All integers (positive, negative, and zero) are rational. For example, 5 can be written as 5/1, -3 as -3/1, and 0 as 0/1.
- Fractions: By definition, all fractions (both proper and improper) with integer numerators and non-zero integer denominators are rational. Examples include 2/3, -7/4, 15/8.
- Terminating Decimals: Decimals that end, such as 0.5 (which is 1/2), 1.75 (which is 7/4), and -0.125 (which is -1/8), are all rational.
- Repeating Decimals: Decimals with a repeating pattern, like 0.333… (which is 1/3), 0.142857142857… (which is 1/7), and 2.666… (which is 8/3), are also rational.
Rational Number Examples – Table Breakdown:
| Numerator (p) | Denominator (q) | Fraction (p/q) | Decimal Form | Rational? |
|---|---|---|---|---|
| 10 | 2 | 10/2 | 5 | Yes |
| 1 | 1000 | 1/1000 | 0.001 | Yes |
| 50 | 10 | 50/10 | 5 | Yes |
| -3 | 7 | -3/7 | -0.428571… (repeating) | Yes |
| 9 | 1 | 9/1 | 9 | Yes |

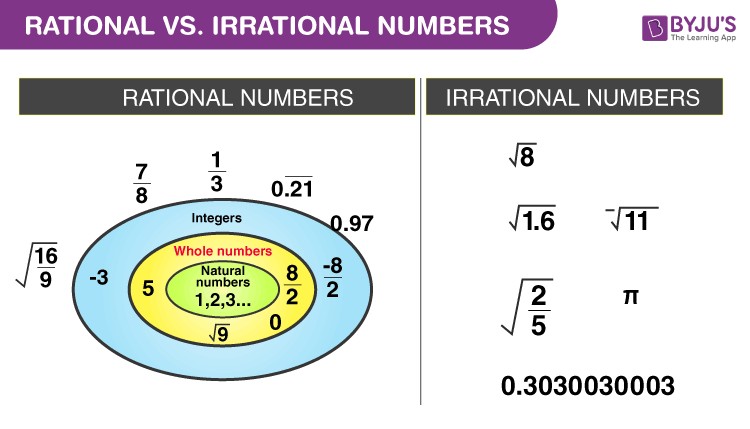

Exploring Types of Rational Numbers
Rational numbers are part of a larger hierarchy of number sets. Understanding their place within these sets helps clarify their nature. The diagram below illustrates this relationship:
- Real Numbers (R): This is the broadest set, encompassing all rational and irrational numbers.
- Rational Numbers (Q): A subset of real numbers, as we’ve been discussing.
- Integers (Z): All whole numbers and their negatives (…, -2, -1, 0, 1, 2, …). Integers are a subset of rational numbers (e.g., 5 = 5/1).
- Whole Numbers (W): Non-negative integers (0, 1, 2, 3, …). Whole numbers are a subset of integers and thus also rational numbers.
- Natural Numbers (N): Positive integers (1, 2, 3, …). Natural numbers are a subset of whole numbers and rational numbers.
Essentially, every natural number, whole number, and integer is also a rational number. This is because they can all be expressed in the form p/q with a denominator of 1.
Standard Form of Rational Numbers: Simplification
A rational number is said to be in its standard form or simplest form when the numerator and denominator have no common factors other than 1, and the denominator is positive. Simplifying a rational number to its standard form makes it easier to compare and work with.
For instance, consider the rational number 12/36. While it is rational, it’s not in standard form because 12 and 36 share common factors (2, 3, 4, 6, 12). To convert it to standard form, we find the greatest common divisor (GCD) of 12 and 36, which is 12. Dividing both the numerator and the denominator by 12, we get (12 ÷ 12) / (36 ÷ 12) = 1/3. Now, 1/3 is in standard form because 1 and 3 have no common factors other than 1, and the denominator (3) is positive.
Positive and Negative Rational Numbers: Sign Matters
Rational numbers can be either positive or negative, just like integers. The sign of a rational number is determined by the signs of its numerator and denominator.
- Positive Rational Numbers: A rational number p/q is positive if both the numerator (p) and the denominator (q) have the same sign (both positive or both negative). For example, 3/5, 12/17, and even (-2)/(-3) (which simplifies to 2/3) are positive rational numbers. Positive rational numbers are always greater than 0.
- Negative Rational Numbers: A rational number p/q is negative if the numerator (p) and the denominator (q) have opposite signs (one positive and one negative). For example, -2/5, 9/-11, and -1/5 are negative rational numbers. Negative rational numbers are always less than 0. It’s important to note that -(p/q), (-p)/q, and p/(-q) all represent the same negative rational number.
| Feature | Positive Rational Numbers | Negative Rational Numbers |
|---|---|---|
| Sign of Numerator & Denominator | Same sign (both + or both -) | Opposite signs (one + and one -) |
| Value | Greater than 0 | Less than 0 |
| Examples | 12/17, 9/11, 3/5, (-4)/(-7) | -2/17, 9/-11, -1/5, (-3)/8 |
Arithmetic Operations with Rational Numbers
Just like with integers and whole numbers, we can perform basic arithmetic operations – addition, subtraction, multiplication, and division – with rational numbers. Let’s explore how these operations work for two rational numbers, say p/q and s/t.
1. Addition: To add two rational numbers, p/q and s/t, we first need to find a common denominator. The easiest common denominator to use is the product of the denominators, q*t. Then, we rewrite each fraction with this common denominator and add the numerators:
(p/q) + (s/t) = (p*t)/(q*t) + (s*q)/(t*q) = (pt + qs) / (qt)
Example: 1/2 + 3/4 = (1*4 + 3*2) / (2*4) = (4 + 6) / 8 = 10/8. This can be simplified to 5/4.
2. Subtraction: Subtraction of rational numbers follows a similar process to addition. Find a common denominator, rewrite the fractions, and subtract the numerators:
(p/q) – (s/t) = (p*t)/(q*t) – (s*q)/(t*q) = (pt – qs) / (qt)
Example: 1/2 – 3/4 = (1*4 – 3*2) / (2*4) = (4 – 6) / 8 = -2/8. This simplifies to -1/4.
3. Multiplication: Multiplying rational numbers is straightforward. Simply multiply the numerators together and the denominators together:
(p/q) * (s/t) = (p*s) / (q*t)
Example: 1/2 * 3/4 = (1*3) / (2*4) = 3/8
4. Division: Dividing rational numbers involves multiplying the first rational number by the reciprocal of the second rational number. The reciprocal of s/t is t/s.
(p/q) ÷ (s/t) = (p/q) * (t/s) = (p*t) / (q*s)
Example: 1/2 ÷ 3/4 = (1/2) * (4/3) = (1*4) / (2*3) = 4/6. This simplifies to 2/3.
Multiplicative Inverse (Reciprocal) of Rational Numbers
The multiplicative inverse or reciprocal of a rational number p/q is obtained by flipping the fraction, resulting in q/p (where p is not zero). When a rational number is multiplied by its multiplicative inverse, the product is always 1.
For example, the multiplicative inverse of 4/7 is 7/4. And indeed, (4/7) * (7/4) = (4*7) / (7*4) = 28/28 = 1.
Key Properties of Rational Numbers
Rational numbers, being a subset of real numbers, inherit many properties of the real number system. Some important properties specific to rational numbers include:
- Closure Property: Rational numbers are closed under addition, subtraction, and multiplication. This means that if you add, subtract, or multiply any two rational numbers, the result will always be another rational number.
- Density Property: Between any two distinct rational numbers, there are infinitely many other rational numbers. This property highlights the continuous nature of rational numbers on the number line.
- Equivalence: A rational number remains unchanged if both its numerator and denominator are multiplied or divided by the same non-zero integer. This is the principle behind simplifying fractions and finding equivalent forms.
- Additive Identity: Zero (0) is the additive identity for rational numbers. Adding zero to any rational number leaves the number unchanged (a + 0 = a).
- Multiplicative Identity: One (1) is the multiplicative identity for rational numbers. Multiplying any rational number by one leaves the number unchanged (a * 1 = a).
For a more in-depth exploration, you can delve into the properties of rational numbers in a dedicated resource.
Rational Numbers vs. Irrational Numbers: Key Differences
The realm of real numbers is divided into two distinct categories: rational numbers and irrational numbers. We’ve extensively discussed rational numbers; now, let’s understand how they differ from irrational numbers.
The fundamental difference lies in their representation as fractions and decimals:
- Rational Numbers: Can be expressed as a fraction p/q (integers p, q; q≠0). Their decimal representations are either terminating or repeating.
- Irrational Numbers: Cannot be expressed as a simple fraction p/q. Their decimal representations are non-terminating and non-repeating (they go on forever without a repeating pattern).
Examples of Irrational Numbers:
- Pi (π): Approximately 3.141592653589… This famous mathematical constant represents the ratio of a circle’s circumference to its diameter.
- Euler’s Number (e): Approximately 2.718281828459… This number is crucial in calculus and other areas of mathematics.
- Square root of 2 (√2): Approximately 1.414213… This is the length of the diagonal of a square with sides of length 1.
- Square root of 3 (√3), Square root of 5 (√5), etc.: Square roots of non-perfect square integers are irrational.
Key Distinctions Summarized:
| Feature | Rational Numbers | Irrational Numbers |
|---|---|---|
| Fraction Form | Can be expressed as p/q | Cannot be expressed as p/q |
| Decimal Representation | Terminating or repeating | Non-terminating and non-repeating |
| Examples | 1/2, -3/4, 0.75, 0.333… | π, e, √2, √3 |
Finding Rational Numbers Between Two Rational Numbers
A fascinating property of rational numbers is their density. Between any two given rational numbers, you can always find infinitely many other rational numbers. Here are two common methods to find rational numbers between two given rational numbers:
Method 1: Using Equivalent Fractions
- Find a Common Denominator: Convert the given rational numbers to equivalent fractions with a common denominator.
- Increase the Denominator (if needed): If the numerators are consecutive or too close to find integers in between, multiply both the numerator and denominator of both fractions by the same integer (like 10, 100, etc.) to create more space between the numerators.
- Identify Intermediate Rational Numbers: Write down rational numbers with the same denominator and numerators that lie between the numerators of the equivalent fractions you found.
Method 2: Using the Mean (Average)
- Calculate the Mean: The mean of two numbers is found by adding them together and dividing by 2. For two rational numbers, a and b, their mean is (a + b) / 2. The mean of two rational numbers is always a rational number that lies between them.
- Repeat for More Numbers: To find more rational numbers, you can repeat this process. Find the mean of one of the original numbers and the newly found mean. You can continue this process to generate as many rational numbers as you need between the original two.
Video Lesson: Visualizing Rational Numbers
[Include Video Here – if available, or link to a relevant video on YouTube about Rational Numbers]
Solved Examples: Putting Concepts into Practice
Let’s work through some examples to solidify your understanding of rational numbers.
Example 1: Identifying Rational vs. Irrational Numbers
Classify each of the following numbers as rational or irrational: ¾, 90/12007, 12, and √5.
Solution:
- ¾: Rational. It is already in the form of a fraction p/q. Decimal form: 0.75 (terminating).
- 90/12007: Rational. It is expressed as a fraction p/q.
- 12: Rational. It can be written as 12/1, which is in the form p/q. Decimal form: 12 (terminating).
- √5: Irrational. The square root of 5 is a non-terminating, non-repeating decimal (approximately 2.2360679775…). It cannot be expressed as a simple fraction.
Example 2: Mixed Fractions and Rationality
Is the mixed fraction 1 1/2 a rational number?
Solution:
First, convert the mixed fraction to an improper fraction: 1 1/2 = (1 * 2 + 1) / 2 = 3/2.
Now, we examine 3/2:
- Numerator = 3 (an integer)
- Denominator = 2 (an integer and not equal to zero)
Since 3/2 fits the definition of a rational number (p/q form), yes, 1 1/2 is a rational number.
Example 3: Decimal Numbers – Rational or Irrational?
Determine whether the following decimal numbers are rational or irrational: (a) 1.75 (b) 0.01 (c) 0.5 (d) 0.09 (e) √3
Solution:
Convert each decimal to fraction form if possible.
| Decimal Number | Fraction Form | Rational? |
|---|---|---|
| (a) 1.75 | 175/100 = 7/4 | Yes |
| (b) 0.01 | 1/100 | Yes |
| (c) 0.5 | 5/10 = 1/2 | Yes |
| (d) 0.09 | 9/100 | Yes |
| (e) √3 | Cannot be expressed as a simple fraction | No (Irrational) |
To further enhance your understanding and practice more problems on rational numbers, consider exploring resources like BYJU’S – The Learning App for detailed explanations and step-by-step solutions. You can also take practice tests to assess your grasp of the concepts.
Frequently Asked Questions (FAQs) About Rational Numbers
Q1: What Are Rational Numbers? Give examples.
A: Rational numbers are numbers that can be expressed in the form p/q, where p and q are integers, and q is not equal to 0. Examples include: 1/3, 2/4 (which simplifies to 1/2), 1/5, 9/3 (which simplifies to 3), -5/7, 0 (which can be written as 0/1).
Q2: What is the difference between rational and irrational numbers?
A: Rational numbers can be expressed as a ratio of two integers (fractions), and their decimal representations are either terminating or repeating. Irrational numbers cannot be expressed as a simple fraction, and their decimal representations are non-terminating and non-repeating. Examples: Rational – 10/2, Irrational – Pi (π) ≈ 3.141592653589…
Q3: Is 0 a rational number?
A: Yes, 0 is a rational number. It is an integer and can be written in the form p/q, such as 0/1, 0/2, etc. Since the denominator can be any non-zero integer, 0 fits the definition of a rational number.
Q4: Is 7 a rational number?
A: Yes, 7 is a rational number. Any integer is a rational number because it can be expressed as a fraction with a denominator of 1. So, 7 can be written as 7/1.
Q5: Is 3.14 a rational number? What about Pi (π)?
A: 3.14 is a rational number because it is a terminating decimal. It can be written as the fraction 314/100 (or 157/50 in simplest form). However, Pi (π) is not a rational number. While 3.14 is a common approximation, the exact value of Pi is 3.141592653589793238… which is a non-terminating, non-repeating decimal, making it irrational.
Q6: Find a rational number between 3 and 4.
A: One way to find a rational number between 3 and 4 is to calculate their mean: (3 + 4) / 2 = 7/2. 7/2 (or 3.5) is a rational number that lies exactly halfway between 3 and 4.
Q7: What can the denominator of a rational number be?
A: The denominator of a rational number can be any integer except 0. It can be positive or negative, but it cannot be zero because division by zero is undefined.
Q8: Is Pi (π) a rational number?
A: No, Pi (π) is definitively not a rational number. It is a famous example of an irrational number. Its decimal representation is non-terminating and non-repeating, and it cannot be expressed as a simple fraction of two integers. Its approximate value is 3.141592653589…