What Does Congruent Mean? Geometry Explained Simply

What Does Congruent Mean in geometry? This is a common question, and at WHAT.EDU.VN, we provide clear, concise answers to help you understand. Learn about congruent figures, their properties, and how they differ from similar figures. Explore congruence postulates and theorems, and discover how this concept is applied in real-world scenarios. Are you struggling to grasp these concepts? Don’t worry, you can ask any question and get free answers on WHAT.EDU.VN. We’ll break it down for you!

1. Understanding Congruent Meaning in Geometry

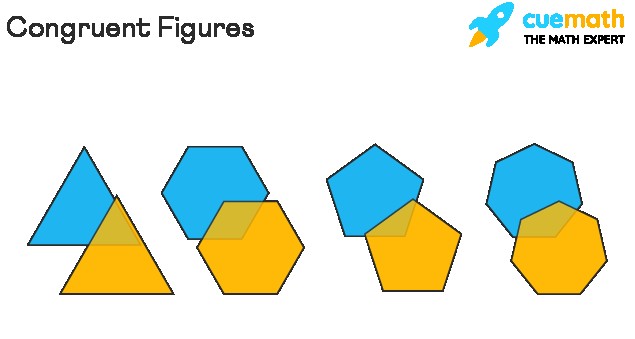
The term ‘congruent’ in geometry signifies that two figures are precisely identical in both shape and size. Think of it as an exact match. The figures can be rotated, flipped, or turned, but if they still match up perfectly, they are congruent. Two geometric figures are congruent if they have the same dimensions. Imagine two identical puzzle pieces; they are congruent. Congruency is a fundamental concept in geometry that helps in understanding shapes and their relationships. Congruent shapes and congruent objects are the same.

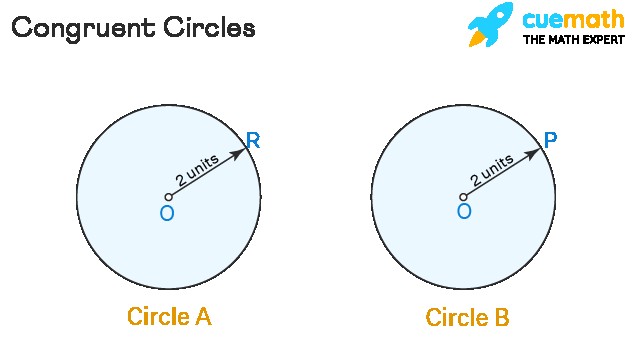
For example, if you draw two circles with the same radius, cut them out, and place one on top of the other, they will perfectly overlap. This demonstrates that the two circles are congruent. The symbol for congruence is “≅”. So, if circle A is congruent to circle B, we write: Circle A ≅ Circle B.

Key Takeaways:

• Congruent figures are identical in shape and size.
• The symbol “≅” denotes congruence.
• Rotation, flipping, or turning doesn’t affect congruence.
• Congruent means exactly equal.
• Discover more on WHAT.EDU.VN

2. Exploring Congruent Figures

Two figures are congruent if they can be perfectly superimposed on each other. This means you can place one figure directly on top of the other, and they will align precisely. The term ‘congruence’ describes the relationship between these figures. This principle applies not only to shapes like triangles and quadrilaterals but also to line segments and angles, provided they have the same measure. This makes understanding shapes easier.

Imagine tracing a shape on a piece of paper, then cutting it out. The original shape and the cutout are congruent.

Key Takeaways:

• Congruent figures can be superimposed on each other.
• The concept applies to shapes, line segments, and angles.
• WHAT.EDU.VN helps you understand congruent relationships.
• Congruent shapes are mirror images if one is flipped.
• Equal parts define congruence.

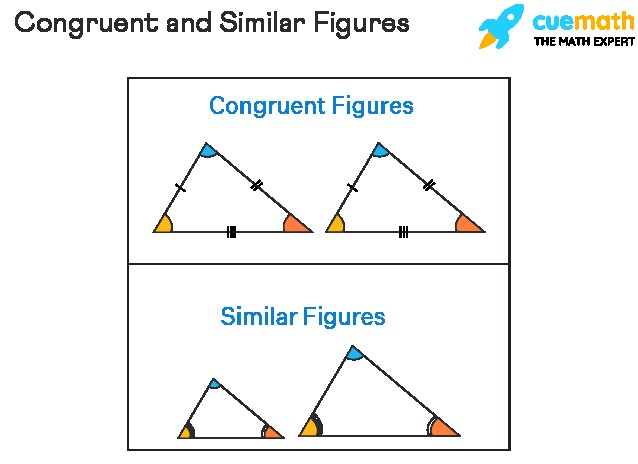
3. Congruent vs. Similar Figures: What’s the Difference?

It’s crucial to distinguish between congruent and similar figures. Congruent figures are exactly the same – same shape, same size. Similar figures, on the other hand, have the same shape, but their sizes can differ. Think of it like this: a photograph and a smaller copy of it are similar, but two identical photographs are congruent. Equal angles are required for similar figures.

In congruent figures, all corresponding sides and angles are equal. In similar figures, corresponding angles are equal, but the corresponding sides are proportional (meaning they have the same ratio). Understanding the difference between these shapes will help when studying geometry.

Key Takeaways:

• Congruent: Same shape and size.
• Similar: Same shape, different size.
• Corresponding sides are equal in congruent figures.
• Corresponding angles are equal in similar figures, but sides are proportional.
• If you’re still confused, ask a question on WHAT.EDU.VN.

4. Diving Deep: Congruence of Triangles

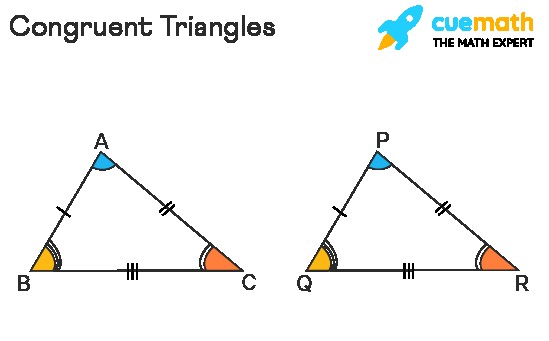
Two triangles are congruent if all their corresponding sides and angles are equal. This also means that one triangle can be perfectly superimposed on the other. To prove that two triangles are congruent, we use congruence theorems or criteria.

Sides: AB = PQ, BC = QR and AC = PR

Angles: ∠A = ∠P, ∠B = ∠Q, and ∠C = ∠R

Therefore, Δ ABC ≅ Δ PQR. There are several theorems for congruent triangles.

Here are the most commonly used congruence theorems:

• SSS (Side, Side, Side): If all three sides of one triangle are equal to the corresponding three sides of another triangle, then the triangles are congruent.
• SAS (Side, Angle, Side): If two sides and the included angle (the angle between those two sides) of one triangle are equal to the corresponding two sides and included angle of another triangle, then the triangles are congruent.
• ASA (Angle, Side, Angle): If two angles and the included side (the side between those two angles) of one triangle are equal to the corresponding two angles and included side of another triangle, then the triangles are congruent.
• AAS (Angle, Angle, Side): If two angles and a non-included side of one triangle are equal to the corresponding two angles and non-included side of another triangle, then the triangles are congruent.
• RHS (Right angle-Hypotenuse-Side): This applies to right-angled triangles. If the hypotenuse and one side of one right-angled triangle are equal to the hypotenuse and corresponding side of another right-angled triangle, then the triangles are congruent. This is also known as the Hypotenuse Leg theorem.

Key Takeaways:

• Triangles are congruent if all corresponding sides and angles are equal.
• Congruence theorems (SSS, SAS, ASA, AAS, RHS) help prove congruence.
• Understanding these theorems simplifies geometry problems.
• Practice applying these theorems to various triangle examples.
• For more help, visit WHAT.EDU.VN and ask away!

5. Real-World Congruent Examples

Congruence isn’t just a theoretical concept; it’s all around us. Here are some examples of congruent shapes and figures in everyday life:

• Tiles: Identical tiles on a floor or wall are congruent. They have the same shape and size, allowing them to fit together perfectly.
• Building Blocks: Sets of building blocks often contain congruent pieces, enabling you to create symmetrical structures.
• Mass-produced Items: Products like screws, bolts, and washers are often manufactured to be congruent, ensuring they are interchangeable.
• Playing Cards: In a deck of cards, all the cards of the same rank and suit (e.g., all the Aces) are congruent.
• Stamps: Identical postage stamps are congruent.

By recognizing congruence in these real-world examples, you can better appreciate its practical applications and deepen your understanding of the concept.

Key Takeaways:

• Congruence is evident in everyday objects.
• Examples include tiles, building blocks, and mass-produced items.
• Recognizing these examples enhances your understanding.
• Consider how congruence simplifies manufacturing and design.
• Got a real-world example you’re unsure about? Ask WHAT.EDU.VN.

6. Side-by-Side: Examples Demystifying Congruence

Let’s solidify your understanding with a couple of detailed examples:

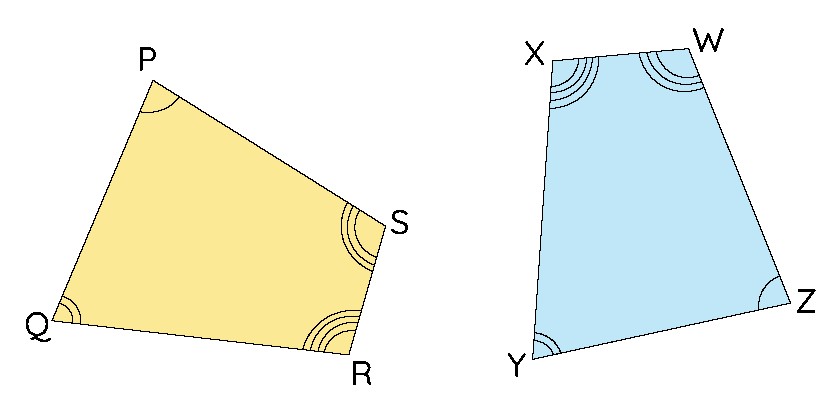
1. Example 1: Quadrilateral Congruence

   Suppose you have two quadrilaterals, PQRS and WXYZ, and you know they are congruent. If angle WXY in quadrilateral WXYZ is marked with four arcs, which angle in quadrilateral PQRS corresponds to it?

   Solution:
   Identify the corresponding parts in both quadrilaterals. If ∠WXY is marked with four arcs, look for the angle in PQRS that is marked in the same way. If ∠QRS is also marked with four arcs, then ∠QRS corresponds to ∠WXY, meaning they are congruent.

2. Example 2: Finding Congruent Squares

   Emma has four squares with the following side lengths:

   • Square A: side = 5 inches
   • Square B: side = 7 inches
   • Square C: side = 5 inches
   • Square D: side = 8 inches

   Which two squares can be placed exactly one over the other?

   Solution:
   Squares that have the same side lengths will superimpose perfectly, meaning they are congruent. Emma needs to find two squares with identical side lengths. In this case, Square A and Square C both have sides of 5 inches. Therefore, Emma can choose Square A and Square C because they are congruent.

Key Takeaways:

• Corresponding parts in congruent figures are equal.
• Matching side lengths indicate congruent squares.
• Visual aids can help identify congruent angles and sides.
• Always look for matching markings or measurements.
• For more examples, ask our community at WHAT.EDU.VN.

7. Congruence Properties: Reflexive, Symmetric, and Transitive

Congruence, like equality, has several important properties that are useful in proofs and problem-solving. These properties apply to lines, angles, and figures:

1. Reflexive Property: Any geometric figure is congruent to itself.

   • For example: Line segment AB ≅ Line segment AB, or ∠P ≅ ∠P.

2. Symmetric Property: If one figure is congruent to another, then the second figure is congruent to the first.

   • For example: If ∠P ≅ ∠Q, then ∠Q ≅ ∠P.

3. Transitive Property: If one figure is congruent to a second figure, and the second figure is congruent to a third figure, then the first figure is congruent to the third figure.

   • For example: If line 1 ≅ line 2, and line 2 ≅ line 3, then line 1 ≅ line 3.

Understanding these properties can simplify complex geometric problems and proofs. They allow you to make logical deductions and establish relationships between different figures.

Key Takeaways:

• Reflexive: A figure is congruent to itself.
• Symmetric: Congruence works in both directions.
• Transitive: Congruence can be chained together.
• These properties aid in geometric proofs.
• Need more clarification? Post your question on WHAT.EDU.VN.

8. Diving Deeper: Common Questions About Congruence

Let’s address some frequently asked questions to enhance your understanding:

Question	Answer
What are congruent figures?	Congruent figures have the same side lengths and angle measures. They can be superimposed perfectly.
How do you prove triangles are congruent?	You can prove triangles congruent using SSS, SAS, ASA, AAS, or RHS congruence theorems.
What shape has all congruent sides?	A square is a classic example of a shape with all congruent sides and equal angles.
Are vertical angles always congruent?	Yes, according to the vertical angles theorem, vertical angles (opposite angles formed by intersecting lines) are always congruent.
What is another word for congruent?	Synonyms for congruent include identical, equal, matching, and coinciding.
What makes angles congruent?	Angles are congruent if their measures (in degrees or radians) are exactly the same.
Are similar figures congruent?	No, similar figures have the same shape but can be different sizes. Congruent figures must have the same shape and size.
Can congruent figures be mirror images?	Yes, congruent figures can be mirror images of each other. They are still considered congruent even if one is flipped or reflected.
Is congruence used outside of geometry?	Yes, congruence is used in various fields like engineering, architecture, and manufacturing to ensure precision and uniformity in designs and products.
How does congruence relate to symmetry?	Congruence is closely related to symmetry. A figure has symmetry if one part of it is congruent to another part (e.g., reflectional symmetry, rotational symmetry).

Key Takeaways:

• Congruence is about exact matching, not just similarity.
• Various theorems and properties help prove congruence.
• Congruence applies in many real-world contexts.
• Understanding these FAQs can clarify common confusions.
• Have more questions? The WHAT.EDU.VN community is here to help!

9. Congruence Theorems Explained: SSS, SAS, ASA, AAS, and RHS

To definitively prove that two triangles are congruent, we rely on several key theorems. Here’s a breakdown:

1. SSS (Side, Side, Side):

   • If all three sides of one triangle are equal in length to the corresponding three sides of another triangle, then the two triangles are congruent.

2. SAS (Side, Angle, Side):

   • If two sides and the included angle (the angle between those sides) of one triangle are equal to the corresponding two sides and included angle of another triangle, then the two triangles are congruent.

3. ASA (Angle, Side, Angle):

   • If two angles and the included side (the side between those angles) of one triangle are equal to the corresponding two angles and included side of another triangle, then the two triangles are congruent.

4. AAS (Angle, Angle, Side):

   • If two angles and a non-included side of one triangle are equal to the corresponding two angles and non-included side of another triangle, then the two triangles are congruent.

5. RHS (Right angle-Hypotenuse-Side):

   • This theorem applies specifically to right-angled triangles. If the hypotenuse and one side of one right-angled triangle are equal to the hypotenuse and corresponding side of another right-angled triangle, then the two triangles are congruent. This is also known as the Hypotenuse Leg Theorem.

Mastering these theorems is essential for solving geometry problems involving triangles. Each theorem provides a specific set of conditions that, when met, guarantee congruence.

Key Takeaways:

• Each theorem has specific requirements for proving congruence.
• SSS relies on three sides, while SAS and ASA use sides and angles.
• AAS and RHS are variations that apply in specific cases.
• Knowing these theorems streamlines problem-solving.
• Need help applying these theorems? Ask an expert on WHAT.EDU.VN!

10. Step-by-Step: Proving Congruence with Examples

Let’s work through some examples to demonstrate how to apply the congruence theorems:

Example 1: Using SSS (Side, Side, Side)

• Given: Triangle ABC and Triangle DEF with AB = DE, BC = EF, and CA = FD.
• Proof:
  • AB = DE (Given)
  • BC = EF (Given)
  • CA = FD (Given)
  • Therefore, Triangle ABC ≅ Triangle DEF (SSS Congruence Theorem)

Example 2: Using SAS (Side, Angle, Side)

• Given: Triangle PQR and Triangle XYZ with PQ = XY, ∠PQR = ∠XYZ, and QR = YZ.
• Proof:
  • PQ = XY (Given)
  • ∠PQR = ∠XYZ (Given)
  • QR = YZ (Given)
  • Therefore, Triangle PQR ≅ Triangle XYZ (SAS Congruence Theorem)

Example 3: Using ASA (Angle, Side, Angle)

• Given: Triangle LMN and Triangle UVW with ∠LMN = ∠UVW, MN = VW, and ∠MNL = ∠VWU.
• Proof:
  • ∠LMN = ∠UVW (Given)
  • MN = VW (Given)
  • ∠MNL = ∠VWU (Given)
  • Therefore, Triangle LMN ≅ Triangle UVW (ASA Congruence Theorem)

By following these step-by-step proofs, you can see how the congruence theorems are applied in practice. Remember to always clearly state the given information and the theorem you are using to justify each step.

Key Takeaways:

• Clearly state the given information.
• Identify which theorem applies based on the given information.
• Write a logical step-by-step proof.
• Practice with various examples to build confidence.
• For personalized help, connect with tutors on WHAT.EDU.VN.

11. Advanced Congruence: Beyond Basic Shapes

While we’ve focused on triangles, congruence extends to other geometric shapes as well. Here’s how:

• Quadrilaterals: Two quadrilaterals are congruent if all four corresponding sides and all four corresponding angles are equal. This means you need to demonstrate eight congruencies in total.
• Circles: Two circles are congruent if they have the same radius. Since all points on a circle are equidistant from the center, knowing the radii are equal is sufficient to prove congruence.
• Polygons: For any polygon, congruence requires that all corresponding sides and angles are equal. This can become quite complex for polygons with many sides.

The underlying principle remains the same: for figures to be congruent, they must be identical in both shape and size. Extending your understanding of congruence to these shapes opens up new possibilities in geometry and related fields.

Key Takeaways:

• Congruence applies to more than just triangles.
• Quadrilaterals require proving equality of sides and angles.
• Circles are congruent if they have the same radius.
• Polygons require all corresponding parts to be equal.
• Explore advanced congruence concepts on WHAT.EDU.VN.

12. Applications of Congruence in Various Fields

Congruence is more than just a theoretical concept; it has practical applications in numerous fields:

• Architecture: Architects use congruence to design symmetrical buildings and structures. Identical windows, doors, and structural elements ensure visual appeal and structural integrity.
• Engineering: Engineers rely on congruence to manufacture interchangeable parts. This ensures that components fit together correctly and that machines function as intended.
• Manufacturing: In mass production, congruence is essential for creating identical products. This allows for quality control and ensures that customers receive consistent items.
• Computer Graphics: Congruence is used in computer graphics to create realistic images and animations. By using congruent shapes and patterns, artists can create visually appealing designs.
• Robotics: Robots use congruence to perform tasks that require precision and accuracy. For example, a robot might use congruent movements to assemble a product or perform a surgical procedure.

By understanding the applications of congruence, you can appreciate its importance in the world around us. It’s a fundamental concept that enables innovation and progress in many different fields.

Key Takeaways:

• Congruence is used in architecture for symmetrical designs.
• Engineering relies on congruence for interchangeable parts.
• Manufacturing uses congruence for mass production.
• Computer graphics and robotics also utilize congruence.
• Discover more real-world applications on WHAT.EDU.VN.

13. Mastering Geometric Proofs: Leveraging Congruence

Geometric proofs often involve demonstrating that two figures are congruent. Here’s a strategy for tackling such proofs:

1. Understand the Given Information: Carefully read the problem and identify what information is provided. Draw a diagram if necessary.

2. Identify What Needs to Be Proven: Clearly state what you need to demonstrate. This will guide your steps.

3. Choose the Appropriate Congruence Theorem: Based on the given information, select the congruence theorem (SSS, SAS, ASA, AAS, RHS) that is most likely to help you prove congruence.

4. Write the Proof Step-by-Step:

   • Start with the given information.
   • Use logical deductions and geometric principles to build your argument.
   • Justify each step with a theorem or definition.
   • End with the statement you were trying to prove.

5. Review Your Proof: Check each step to ensure it is logically sound and supported by a valid reason.

By following these steps, you can approach geometric proofs with confidence and demonstrate your understanding of congruence.

Key Takeaways:

• Start by understanding the given information.
• Choose the appropriate congruence theorem.
• Write a step-by-step proof with justifications.
• Review your proof for accuracy.
• Get expert help with proofs on WHAT.EDU.VN.

14. Visual Learning: Diagrams and Congruence

Visual aids are incredibly helpful for understanding congruence. Diagrams allow you to see the relationships between figures and identify corresponding parts.

Here are some tips for using diagrams effectively:

• Draw Accurate Diagrams: Use a ruler and protractor to create accurate diagrams that reflect the given information.
• Label Corresponding Parts: Clearly label corresponding sides and angles with the same markings (e.g., tick marks for equal sides, arcs for equal angles).
• Use Color Coding: Use different colors to highlight congruent parts or different triangles, making it easier to see the relationships.
• Redraw Complex Diagrams: If a diagram is too cluttered or confusing, redraw it with only the essential information.

By using diagrams effectively, you can enhance your understanding of congruence and make it easier to solve geometry problems.

Key Takeaways:

• Draw accurate and well-labeled diagrams.
• Use color coding to highlight congruent parts.
• Redraw complex diagrams for clarity.
• Visual aids improve understanding and problem-solving.
• Find helpful diagrams and explanations on WHAT.EDU.VN.

15. Congruence in Coordinate Geometry: A Modern Perspective

Congruence isn’t limited to traditional geometric shapes. In coordinate geometry, we can determine congruence using coordinates and distances:

1. Distance Formula: To prove that two line segments are congruent, calculate their lengths using the distance formula:

   • d = √((x₂ – x₁)² + (y₂ – y₁)²). If the distances are equal, the line segments are congruent.

2. Transformations: Congruence is preserved under transformations such as translations, rotations, and reflections. This means if you apply these transformations to a figure, the resulting figure will be congruent to the original.

3. Corresponding Parts: Identify corresponding vertices and sides of the figures. Calculate the distances between corresponding vertices to determine if the corresponding sides are congruent.

4. Coordinate Proofs: Use coordinate proofs to demonstrate congruence by showing that corresponding sides and angles have equal measures using coordinate geometry techniques.

Using coordinate geometry provides a powerful way to prove congruence using algebraic methods.

Key Takeaways:

• Use the distance formula to prove line segments congruent.
• Congruence is preserved under translations, rotations, and reflections.
• Identify and compare corresponding vertices and sides.
• Coordinate proofs offer an algebraic approach to congruence.
• Explore coordinate geometry and congruence on WHAT.EDU.VN.

16. Pitfalls to Avoid When Working with Congruence

Understanding common mistakes can help you avoid them:

1. Assuming Congruence: Don’t assume figures are congruent just because they look similar. Always rely on given information and theorems to prove congruence.
2. Misinterpreting Theorems: Make sure you understand the conditions of each congruence theorem (SSS, SAS, ASA, AAS, RHS) and apply them correctly.
3. Ignoring Corresponding Parts: Always identify and compare corresponding sides and angles when proving congruence.
4. Incorrect Labeling: Label diagrams accurately to avoid confusion and ensure you are comparing the correct parts.
5. Skipping Steps in Proofs: Write out each step in your proofs clearly and justify it with a valid theorem or definition. Don’t skip steps or make logical leaps.

By being aware of these pitfalls, you can approach congruence problems with greater accuracy and avoid common errors.

Key Takeaways:

• Don’t assume congruence without proof.
• Understand and apply congruence theorems correctly.
• Always identify and compare corresponding parts.
• Label diagrams accurately and avoid skipping steps.
• Find more tips and tricks on WHAT.EDU.VN.

17. Mnemonics and Memory Aids for Congruence Theorems

Using mnemonics can help you remember the congruence theorems:

1. SSS (Side, Side, Side): “Super Simple Sides” – emphasizes that all three sides must match.
2. SAS (Side, Angle, Side): “Sandwich Angle Side” – the angle is sandwiched between the two sides.
3. ASA (Angle, Side, Angle): “Angle’s Sweet Arrangement” – the side is arranged between the two angles.
4. AAS (Angle, Angle, Side): “Angels Always Sing” – helps to remember the order of angles and side.
5. RHS (Right angle-Hypotenuse-Side): “Right Hypotenuse Side” – specific to right triangles, listing the key components.

These mnemonics provide a fun and memorable way to recall the conditions required for each congruence theorem, making it easier to apply them in problems.

Key Takeaways:

• Use mnemonics to remember congruence theorems.
• Create your own mnemonics for personalized learning.
• Mnemonics make learning fun and memorable.
• Share your mnemonics with others on WHAT.EDU.VN.
• These are helpful for understanding the relationships.

18. Overcoming Challenges in Congruence Problems

Encountering difficulties is part of the learning process. Here’s how to overcome common challenges:

1. Break Down Complex Problems: Divide complex problems into smaller, more manageable steps.
2. Review Definitions and Theorems: Ensure you have a solid understanding of the basic definitions and theorems related to congruence.
3. Practice Regularly: Consistent practice is key to mastering congruence problems. Work through a variety of examples to build your skills.
4. Seek Help When Needed: Don’t hesitate to ask for help from teachers, tutors, or online resources like WHAT.EDU.VN.
5. Use Different Learning Styles: Experiment with different learning styles, such as visual aids, hands-on activities, or group discussions, to find what works best for you.

By adopting these strategies, you can overcome challenges and build your confidence in solving congruence problems.

Key Takeaways:

• Break down complex problems into smaller steps.
• Review definitions and theorems regularly.
• Practice consistently and seek help when needed.
• Experiment with different learning styles.
• WHAT.EDU.VN offers support and resources for learners.

19. Congruence and Transformations: Maintaining Shape and Size

Transformations play a crucial role in understanding congruence. When a figure undergoes a transformation like a translation, rotation, or reflection, its shape and size remain unchanged. This means that the original figure and the transformed figure are congruent.

• Translation: Moving a figure without changing its orientation.
• Rotation: Turning a figure around a fixed point.
• Reflection: Flipping a figure over a line.

Understanding how transformations preserve congruence is essential for solving problems in coordinate geometry and visualizing geometric relationships.

Key Takeaways:

• Translations, rotations, and reflections preserve congruence.
• The original and transformed figures are congruent.
• Transformations help visualize geometric relationships.
• Explore transformations and congruence on WHAT.EDU.VN.
• Symmetry is maintained under transformations.

20. Want to Ask Questions About Congruence?

Having trouble understanding the nuances of congruence? Don’t worry! WHAT.EDU.VN provides a platform where you can ask any question and get free answers from experts and fellow learners. Our community is dedicated to helping you succeed in geometry and beyond. We are available 24 hours a day, 7 days a week.

Here’s how you can benefit from WHAT.EDU.VN:

• Ask Questions for Free: Post your questions about congruence or any other topic and receive helpful responses.
• Get Expert Answers: Our community includes experienced educators and professionals who can provide clear and accurate explanations.
• Connect with Other Learners: Interact with other students who are also studying congruence and share insights and tips.
• Access a Variety of Resources: Explore our library of articles, tutorials, and videos to enhance your understanding of congruence and other mathematical concepts.

Don’t let confusion hold you back. Join the WHAT.EDU.VN community today and get the support you need to master congruence!

We are located at 888 Question City Plaza, Seattle, WA 98101, United States. Contact us on Whatsapp: +1 (206) 555-7890 or visit our website: WHAT.EDU.VN.

Key Takeaways:

• Ask questions for free on WHAT.EDU.VN.
• Get expert answers and connect with other learners.
• Access a variety of learning resources.
• Overcome challenges and build your confidence.
• Join our community and succeed in geometry!

Remember, understanding “what does congruent mean” is just the beginning. There’s a whole world of geometry waiting to be explored, and what.edu.vn is here to guide you every step of the way. So, don’t hesitate—ask your questions, explore our resources, and become a geometry master today!