Have you ever wondered how to represent the fraction 1/4 as a decimal? It’s a common question! Imagine you have a quarter of a pizza. How would you write that as a number with a decimal point? Let’s explore how to convert 1/4 to its decimal equivalent.
Understanding Fractions and Decimals
Fractions and decimals are two different ways of representing parts of a whole. A fraction shows a portion of something (like 1/4 of a donut), while a decimal uses a base-10 system to show the same portion. Converting between them is a useful skill in everyday life. The key is to understand that converting a fraction to a decimal is all about finding an equivalent form where the denominator is effectively ‘1’.
Converting 1/4 to a Decimal: Two Easy Methods
There are two primary ways to convert the fraction (dfrac{1}{4}) into a decimal. Let’s examine each method:
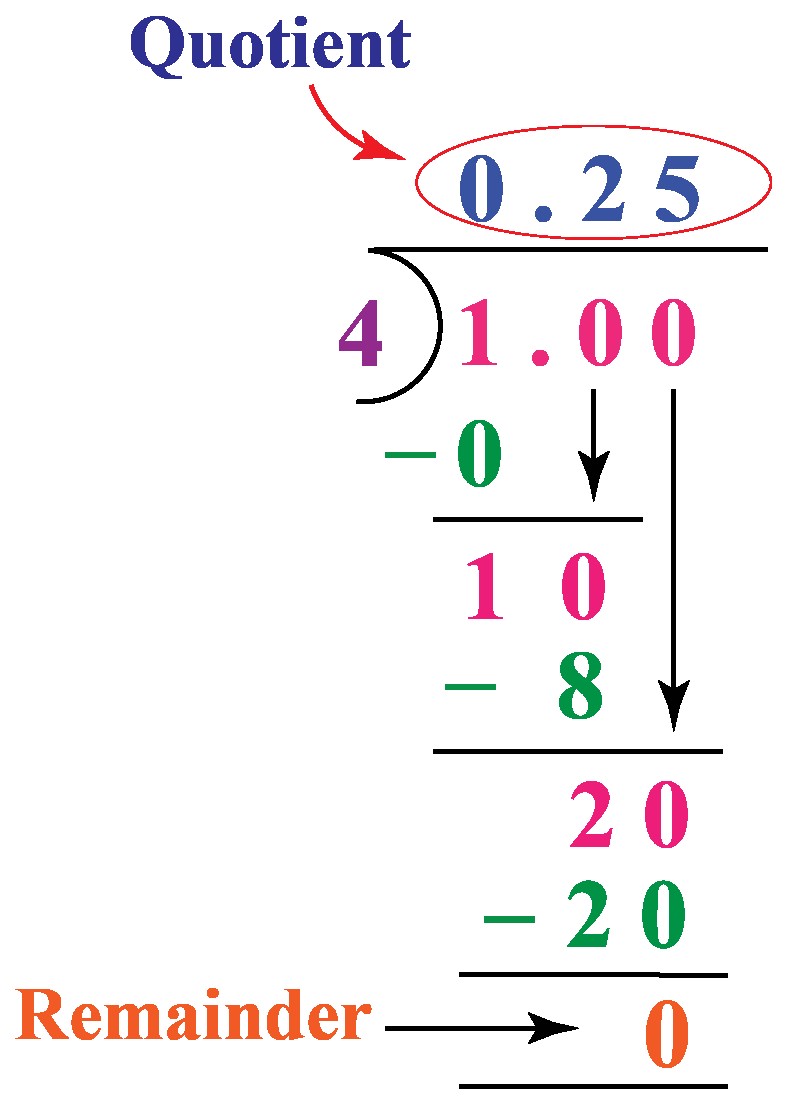
Method 1: Long Division
This method involves dividing the numerator (1) by the denominator (4).
When you perform the long division, you’ll find that 1 divided by 4 equals 0.25. Therefore:
(dfrac{1}{4} = 0.25)
Long division can be applied to convert virtually any fraction into its decimal form.
Method 2: Creating an Equivalent Fraction
This method involves finding an equivalent fraction where the denominator is a power of 10 (like 10, 100, 1000, etc.). Since 4 is a factor of 100, we can easily convert the denominator.
To make the denominator 100, we multiply both the numerator and the denominator of (dfrac{1}{4}) by 25:
begin{align} dfrac{1}{4}&=dfrac{1times 25}{4times 25}\&=dfrac{25}{100}end{align}
Now, since 100 has two zeros, we know there will be two digits after the decimal point in the numerator. Thus:
(dfrac{1}{4} = 0.25)
Converting Other Fractions to Decimals
Let’s look at converting (dfrac{3}{8}) into a decimal, to extend your understanding:
begin{align} dfrac{3}{8}&=dfrac{3times 125}{8times 125}\&=dfrac{375}{1000}\&=0.375end{align}
Converting Decimals to Fractions
You can reverse the process and convert decimals back to fractions. The number of digits after the decimal point determines the denominator (a power of 10).
For example, to convert 0.65 to a fraction:
begin{align} 0.65&= dfrac{65}{100}\&=dfrac{13}{20}end{align}
Alt text: Quick reminders about decimals, fractions, and their relationship.
Real-World Applications
Understanding how to convert fractions to decimals is very useful. Common examples include:
- Calculating discounts: If an item is 1/4 off, you can easily calculate the discount as 0.25 of the original price.
- Measuring ingredients: Recipes often use fractions, and converting them to decimals can make measuring easier.
- Understanding statistics: Many statistics are presented as decimals or percentages, which are closely related to fractions.
Examples
Example 1: Express (dfrac{2}{3}) as a decimal.
Using long division, (dfrac{2}{3}) = 0.6666… which can be rounded to 0.67.
Example 2: Convert (dfrac{3}{8}) to a decimal.
Dividing 3 by 8 gives you 0.375.
Conclusion
Converting (dfrac{1}{4}) to a decimal is straightforward: it’s 0.25. Whether you use long division or create an equivalent fraction, the result is the same. Understanding this conversion, and similar conversions for other fractions, allows you to easily work with fractions and decimals in many practical situations. With this knowledge, you can confidently tackle problems involving fractions and decimals!