What Is 5/8 As A Decimal? Are you looking for a simple and clear explanation? At WHAT.EDU.VN, we provide free answers to all your questions, offering easy-to-understand solutions. Discover the decimal equivalent of fractions, understand the division method, and explore related concepts like converting fractions to decimals and understanding place value.
1. Understanding Fractions and Decimals
Fractions and decimals are two different ways of representing parts of a whole. A fraction is written as one number over another, like 5/8, where 5 is the numerator and 8 is the denominator. It represents 5 parts out of 8 total parts. A decimal, on the other hand, uses a decimal point to separate the whole number part from the fractional part, like 0.625. Both fractions and decimals can express the same value, just in different formats.
Think of a pizza cut into 8 equal slices. If you eat 5 of those slices, you’ve eaten 5/8 of the pizza. The decimal 0.625 represents the same amount – a little more than half of the pizza. Understanding this equivalence is key to working with both fractions and decimals effectively. Knowing how to convert between the two allows you to choose the representation that is most convenient for a particular situation, whether it’s cooking, measuring, or solving math problems.
2. Converting 5/8 to a Decimal: The Division Method
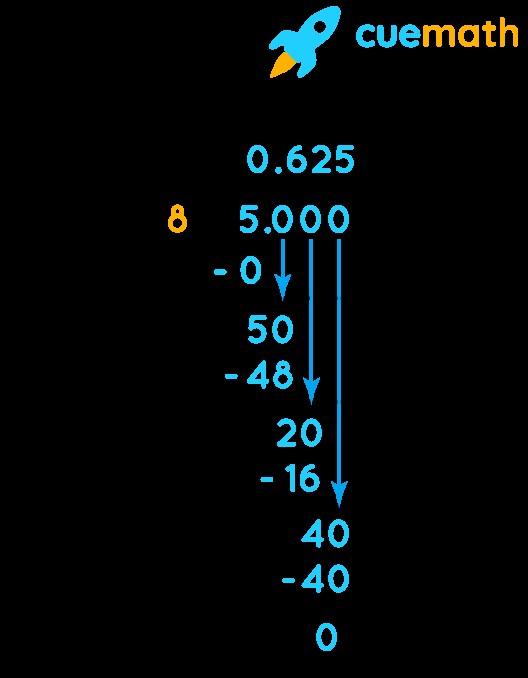
The most straightforward way to convert a fraction to a decimal is by dividing the numerator (the top number) by the denominator (the bottom number). In the case of 5/8, this means dividing 5 by 8. Let’s break down the steps:
- Step 1: Set up the division problem. You’ll be dividing 5 (the numerator) by 8 (the denominator).
- Step 2: Since 8 doesn’t go into 5, add a decimal point and a zero to the right of the 5, making it 5.0.
- Step 3: Now, divide 8 into 50. 8 goes into 50 six times (6 x 8 = 48). Write the 6 after the decimal point in your answer (0.6).
- Step 4: Subtract 48 from 50, which leaves a remainder of 2.
- Step 5: Add another zero to the right of the remainder, making it 20.
- Step 6: Divide 8 into 20. 8 goes into 20 two times (2 x 8 = 16). Write the 2 after the 6 in your answer (0.62).
- Step 7: Subtract 16 from 20, which leaves a remainder of 4.
- Step 8: Add another zero to the right of the remainder, making it 40.
- Step 9: Divide 8 into 40. 8 goes into 40 five times (5 x 8 = 40). Write the 5 after the 2 in your answer (0.625).
- Step 10: Since there is no remainder, you’re done. The decimal equivalent of 5/8 is 0.625.
This division method works for converting any fraction to a decimal. Simply divide the numerator by the denominator, adding zeros as needed until you reach a remainder of zero or the desired level of precision.
3. Understanding the Decimal Value of 5/8
The decimal 0.625 represents six hundred twenty-five thousandths. This means that if you were to divide something into 1000 equal parts, 0.625 would represent 625 of those parts. It’s a bit more than half, as 0.5 would be exactly half.
To further understand the value, you can relate it to other common fractions and decimals. For example, 1/2 is equal to 0.5, and 3/4 is equal to 0.75. Since 5/8 falls between 1/2 and 3/4, the decimal value of 0.625 makes sense. It’s greater than 0.5 but less than 0.75.
Visual aids, such as number lines or pie charts, can also help solidify the understanding of the decimal value. On a number line, 0.625 would be located between 0.5 and 0.75, closer to 0.5. In a pie chart, 5/8 would represent a portion of the pie that is slightly larger than half.
4. Real-World Applications of Converting 5/8 to a Decimal
Knowing how to convert fractions to decimals is useful in many real-world situations. Here are a few examples:
- Cooking and Baking: Recipes often use fractions for ingredients. If you need to double a recipe that calls for 5/8 cup of flour, you’ll need to know the decimal equivalent (0.625) to accurately measure the correct amount (1.25 cups).
- Construction and Carpentry: When measuring materials, fractions are common. If you need to cut a piece of wood that is 5/8 of an inch thick, knowing the decimal equivalent (0.625 inches) can help you use a measuring tool more accurately.
- Finance: Interest rates are often expressed as decimals. If you’re calculating interest on a loan or investment, you may need to convert fractions to decimals to perform the calculations. For example, an interest rate of 5/8 percent would be 0.00625 as a decimal.
- Science and Engineering: Many scientific and engineering calculations involve both fractions and decimals. Being able to convert between the two is essential for accurate measurements and problem-solving.
 5/8 as a decimal example in cooking
5/8 as a decimal example in cooking
5. Tips and Tricks for Fraction to Decimal Conversions
While dividing the numerator by the denominator always works, there are some tips and tricks that can make fraction to decimal conversions easier:
- Memorize Common Equivalents: It’s helpful to memorize the decimal equivalents of common fractions like 1/2 (0.5), 1/4 (0.25), 3/4 (0.75), and 1/8 (0.125). This can speed up calculations and provide a quick reference point.
- Look for Simplification: Before dividing, see if you can simplify the fraction. For example, if you had 10/16, you could simplify it to 5/8 by dividing both the numerator and denominator by 2. This makes the division easier.
- Use Benchmarks: If you’re not sure of the exact decimal equivalent, use benchmark fractions to estimate. For example, if you know that 1/2 is 0.5 and 3/4 is 0.75, you can estimate that 5/8 (which falls between these two fractions) will be somewhere between 0.5 and 0.75.
- Use a Calculator: When accuracy is crucial or the fraction is complex, don’t hesitate to use a calculator. Most calculators have a fraction function that can convert fractions to decimals with ease.
- Practice Regularly: The more you practice converting fractions to decimals, the more comfortable and confident you’ll become. Try converting fractions you encounter in everyday life, such as in recipes or measurements.
6. Common Mistakes to Avoid When Converting Fractions to Decimals
Converting fractions to decimals is a fundamental skill, but it’s easy to make mistakes if you’re not careful. Here are some common errors to avoid:
- Dividing the Denominator by the Numerator: Remember to always divide the numerator (the top number) by the denominator (the bottom number). Dividing the other way around will give you the wrong answer.
- Misplacing the Decimal Point: Pay close attention to the placement of the decimal point. Make sure you add it after the whole number part and keep it aligned as you perform the division.
- Rounding Errors: If the decimal repeats or continues for a long time, you may need to round it to a certain number of decimal places. Be sure to follow the rounding rules correctly (e.g., round up if the next digit is 5 or greater, round down if it’s less than 5).
- Forgetting to Simplify: Simplifying the fraction before dividing can make the calculation easier and reduce the chance of errors. Always check if the fraction can be simplified before you start dividing.
- Not Checking Your Answer: It’s always a good idea to check your answer, especially if you’re working on an important problem. You can use a calculator or estimate to see if your answer makes sense.
7. Exploring Other Fractions and Their Decimal Equivalents
Converting 5/8 to a decimal is a great starting point, but there are many other fractions with interesting decimal equivalents. Here are a few examples:
- 1/3: This fraction has a repeating decimal equivalent of 0.3333… The 3s go on forever.
- 2/3: Similar to 1/3, this fraction has a repeating decimal equivalent of 0.6666… The 6s go on forever.
- 1/6: This fraction has a repeating decimal equivalent of 0.1666… The 6s go on forever.
- 1/7: This fraction has a repeating decimal equivalent of 0.142857142857… The sequence “142857” repeats indefinitely.
- 1/9: This fraction has a repeating decimal equivalent of 0.1111… The 1s go on forever.
These examples illustrate that some fractions have terminating decimals (like 5/8 = 0.625), while others have repeating decimals. Understanding the difference between these types of decimals can help you work with fractions and decimals more effectively.
8. Understanding Terminating and Repeating Decimals
When converting fractions to decimals, you’ll encounter two main types of decimals: terminating and repeating.
- Terminating Decimals: These decimals have a finite number of digits. In other words, they end after a certain number of decimal places. Examples include 1/2 = 0.5, 1/4 = 0.25, and 5/8 = 0.625. Terminating decimals occur when the denominator of the simplified fraction has only 2 and/or 5 as prime factors.
- Repeating Decimals: These decimals have a digit or a group of digits that repeat indefinitely. Examples include 1/3 = 0.3333…, 2/3 = 0.6666…, and 1/7 = 0.142857142857… Repeating decimals occur when the denominator of the simplified fraction has prime factors other than 2 and 5.
It’s important to recognize the difference between terminating and repeating decimals because they require different methods of representation. Terminating decimals can be written exactly, while repeating decimals are often written with a bar over the repeating digit(s) or rounded to a certain number of decimal places.
9. Using Decimals in Measurement Systems
Decimals play a crucial role in various measurement systems, particularly the metric system. The metric system is based on powers of 10, which makes it easy to work with decimals. Here are a few examples:
- Length: In the metric system, the base unit of length is the meter (m). Smaller units, such as centimeters (cm) and millimeters (mm), are defined as decimal fractions of a meter (1 cm = 0.01 m, 1 mm = 0.001 m).
- Weight: In the metric system, the base unit of mass is the gram (g). Larger units, such as kilograms (kg), are defined as decimal multiples of a gram (1 kg = 1000 g).
- Volume: In the metric system, the base unit of volume is the liter (L). Smaller units, such as milliliters (mL), are defined as decimal fractions of a liter (1 mL = 0.001 L).
The use of decimals in the metric system simplifies conversions and calculations. For example, to convert 2.5 meters to centimeters, you simply multiply by 100 (2.5 m x 100 = 250 cm).
10. Converting Decimals to Fractions
Just as it’s important to know how to convert fractions to decimals, it’s also useful to know how to convert decimals to fractions. Here’s how:
- Step 1: Write the decimal as a fraction with a denominator of 1. For example, 0.625 can be written as 0.625/1.
- Step 2: Multiply both the numerator and denominator by a power of 10 to eliminate the decimal point. The power of 10 should be equal to the number of decimal places. In this case, there are three decimal places, so we multiply by 1000: (0.625 x 1000) / (1 x 1000) = 625/1000.
- Step 3: Simplify the fraction by dividing both the numerator and denominator by their greatest common factor (GCF). The GCF of 625 and 1000 is 125. So, we divide both by 125: (625 ÷ 125) / (1000 ÷ 125) = 5/8.
Therefore, the fraction equivalent of 0.625 is 5/8. This process can be used to convert any terminating decimal to a fraction.
11. Understanding Place Value in Decimals
Place value is a fundamental concept in mathematics that applies to both whole numbers and decimals. In a decimal number, each digit has a specific place value that determines its contribution to the overall value of the number.
- The Decimal Point: The decimal point separates the whole number part from the fractional part.
- Places to the Left of the Decimal Point: These places represent whole numbers and have the same place values as in whole numbers (ones, tens, hundreds, thousands, etc.).
- Places to the Right of the Decimal Point: These places represent fractional parts and have place values that are powers of 1/10 (tenths, hundredths, thousandths, ten-thousandths, etc.).
In the decimal 0.625:
- The 6 is in the tenths place, so it represents 6/10 or 0.6.
- The 2 is in the hundredths place, so it represents 2/100 or 0.02.
- The 5 is in the thousandths place, so it represents 5/1000 or 0.005.
Understanding place value helps you read, write, and compare decimals accurately. It also helps you perform operations with decimals, such as addition, subtraction, multiplication, and division.
12. Decimals and Percentages
Decimals and percentages are closely related. A percentage is simply a decimal multiplied by 100. To convert a decimal to a percentage, you multiply it by 100 and add the percent sign (%). To convert a percentage to a decimal, you divide it by 100 and remove the percent sign.
For example, to convert the decimal 0.625 to a percentage, you multiply it by 100: 0.625 x 100 = 62.5%. Therefore, 0.625 is equal to 62.5%.
Percentages are often used to express proportions, rates, and changes. For example, if you get 80 out of 100 questions correct on a test, you can say that you scored 80%. This is the same as saying that you scored 0.80 as a decimal.
13. Rounding Decimals
Rounding decimals is the process of approximating a decimal number to a certain number of decimal places. This is often done to simplify calculations or to present data in a more concise way. Here are the basic rules for rounding decimals:
- Identify the Rounding Place: Determine which decimal place you want to round to (e.g., tenths, hundredths, thousandths).
- Look at the Digit to the Right: Look at the digit immediately to the right of the rounding place.
- Rounding Rules:
- If the digit to the right is 5 or greater, round up the digit in the rounding place.
- If the digit to the right is less than 5, leave the digit in the rounding place as it is.
For example, to round 0.625 to the nearest hundredth (two decimal places):
- The rounding place is the hundredths place (2).
- The digit to the right is 5.
- Since 5 is 5 or greater, round up the 2 to a 3.
Therefore, 0.625 rounded to the nearest hundredth is 0.63.
14. Comparing Decimals
Comparing decimals involves determining which of two or more decimal numbers is greater or smaller. Here’s how to compare decimals:
- Line Up the Decimal Points: Write the decimals vertically, aligning the decimal points.
- Add Zeros as Needed: If the decimals have different numbers of decimal places, add zeros to the right of the shorter decimal so that they have the same number of decimal places.
- Compare Digit by Digit: Starting from the left, compare the digits in each place value. The decimal with the larger digit in the first different place value is the larger decimal.
For example, to compare 0.625 and 0.63:
- Line up the decimal points:
0.625 0.63 - Add a zero to 0.63:
0.625 0.630 - Compare digit by digit:
- The tenths place is the same (6).
- The hundredths place is different (2 vs. 3).
- Since 3 is greater than 2, 0.63 is greater than 0.625.
15. Adding and Subtracting Decimals
Adding and subtracting decimals is similar to adding and subtracting whole numbers, but you need to make sure to align the decimal points. Here’s how:
- Line Up the Decimal Points: Write the decimals vertically, aligning the decimal points.
- Add Zeros as Needed: If the decimals have different numbers of decimal places, add zeros to the right of the shorter decimal so that they have the same number of decimal places.
- Add or Subtract as Usual: Add or subtract the digits in each place value, starting from the right. Carry or borrow as needed.
- Bring Down the Decimal Point: Bring down the decimal point into the answer, making sure it’s aligned with the decimal points in the original numbers.
For example, to add 0.625 and 0.35:
- Line up the decimal points:
0.625 + 0.35 - Add a zero to 0.35:
0.625 + 0.350 - Add as usual:
0.625 + 0.350 ------- 0.975
Therefore, 0.625 + 0.35 = 0.975.
16. Multiplying Decimals
Multiplying decimals is similar to multiplying whole numbers, but you need to keep track of the decimal point. Here’s how:
- Multiply as Usual: Multiply the numbers as if they were whole numbers, ignoring the decimal points.
- Count Decimal Places: Count the total number of decimal places in the original numbers.
- Place the Decimal Point: Place the decimal point in the answer so that it has the same number of decimal places as the total number of decimal places in the original numbers.
For example, to multiply 0.625 and 0.4:
- Multiply as usual:
625 x 4 ----- 2500 - Count decimal places: 0.625 has 3 decimal places, and 0.4 has 1 decimal place, for a total of 4 decimal places.
- Place the decimal point: Place the decimal point in 2500 so that it has 4 decimal places: 0.2500.
Therefore, 0.625 x 0.4 = 0.25.
17. Dividing Decimals
Dividing decimals requires a bit more care than multiplying, adding, or subtracting. Here’s how to divide decimals:
- Make the Divisor a Whole Number: If the divisor (the number you’re dividing by) is a decimal, move the decimal point to the right until it becomes a whole number.
- Move the Decimal Point in the Dividend: Move the decimal point in the dividend (the number you’re dividing into) the same number of places to the right.
- Divide as Usual: Divide as you would with whole numbers.
- Bring Up the Decimal Point: Bring the decimal point up into the quotient (the answer), making sure it’s aligned with the new decimal point in the dividend.
For example, to divide 0.75 by 0.25:
- Make the divisor a whole number: Move the decimal point in 0.25 two places to the right to get 25.
- Move the decimal point in the dividend: Move the decimal point in 0.75 two places to the right to get 75.
- Divide as usual: 75 ÷ 25 = 3.
- Bring up the decimal point: Since we moved the decimal point two places in both the divisor and dividend, the decimal point in the quotient stays in the same relative position.
Therefore, 0.75 ÷ 0.25 = 3.
18. Converting Fractions and Decimals on a Number Line
A number line is a visual tool that can help you understand the relationship between fractions and decimals. To represent fractions and decimals on a number line:
- Draw a Number Line: Draw a horizontal line and mark off equal intervals.
- Label the Endpoints: Label the endpoints of the number line with 0 and 1.
- Divide the Number Line: Divide the number line into equal parts based on the denominator of the fraction. For example, if you want to represent 1/4, divide the number line into four equal parts.
- Mark the Fractions: Mark the fractions on the number line at the appropriate intervals.
- Mark the Decimals: Mark the decimals on the number line at the corresponding locations. For example, 0.25 would be marked at the same location as 1/4.
Using a number line can help you visualize the relative sizes of fractions and decimals and understand how they relate to each other.
19. Fraction and Decimal Games and Activities
Learning about fractions and decimals doesn’t have to be boring. There are many fun and engaging games and activities that can help you master these concepts:
- Fraction Bingo: Create bingo cards with fractions and decimals. Call out fractions or decimals and have players mark them off on their cards.
- Decimal Matching Game: Create pairs of cards with matching fractions and decimals. Have players match the pairs.
- Fraction War: Deal out a deck of cards with fractions. Each player flips over a card, and the player with the larger fraction wins the round.
- Decimal Scavenger Hunt: Hide objects around the room and label them with decimal values. Have players find the objects and add up their values.
- Online Fraction and Decimal Games: There are many websites and apps that offer interactive games and activities for learning about fractions and decimals.
These games and activities can make learning about fractions and decimals more enjoyable and effective.
20. Advanced Fraction and Decimal Concepts
Once you have a solid understanding of the basics of fractions and decimals, you can explore more advanced concepts, such as:
- Scientific Notation: Scientific notation is a way of writing very large or very small numbers using powers of 10. It’s often used in science and engineering.
- Rational and Irrational Numbers: Rational numbers are numbers that can be expressed as a fraction, while irrational numbers cannot. Decimals of rational numbers either terminate or repeat, while decimals of irrational numbers go on forever without repeating.
- Complex Numbers: Complex numbers are numbers that have a real part and an imaginary part. They are often used in advanced mathematics and physics.
- Number Theory: Number theory is a branch of mathematics that deals with the properties of numbers, including fractions and decimals.
These advanced concepts can help you deepen your understanding of mathematics and its applications.
Do you have more questions about fractions, decimals, or any other topic? Don’t hesitate to ask at WHAT.EDU.VN. Our community of experts is here to provide free answers and help you learn. We’re located at 888 Question City Plaza, Seattle, WA 98101, United States. You can also reach us on Whatsapp at +1 (206) 555-7890. Visit our website at WHAT.EDU.VN for more information. Get the answers you need quickly and easily at what.edu.vn.