What Is A 1 To 1 Function? This is a common question, and WHAT.EDU.VN is here to provide a clear answer. One-to-one functions ensure each input has a unique output, offering valuable insights in mathematics. Discover the concept, properties, and real-world applications to enhance your understanding of injective functions and their significance.
1. What Is a One to One Function?
A one to one function, also known as an injective function, is a special type of function where each element in the range (output) corresponds to exactly one element in the domain (input). This means that no two different inputs will produce the same output. Understanding this concept is crucial in various mathematical fields.
1.1. One to One Function Definition
A one to one function ensures that every element in its range corresponds to exactly one element in its domain, preventing outputs from repeating. For example, the function ( g(x) = x + 5 ) is a one to one function because each input ( x ) produces a unique output. In contrast, ( g(x) = x^2 ) is not a one to one function because both ( x = 2 ) and ( x = -2 ) produce the same output, 4. Functions that are not one-to-one are known as many-to-one functions.
Algebraically, a function ( g: D rightarrow F ) is one-to-one if:
[
g(x_1) = g(x_2) Rightarrow x_1 = x_2
]
for all elements ( x_1 ) and ( x_2 ) in ( D ). This condition is also known as injectivity. The contrapositive of this definition is equally valid:
[
x_1 neq x_2 Rightarrow g(x_1) neq g(x_2)
]
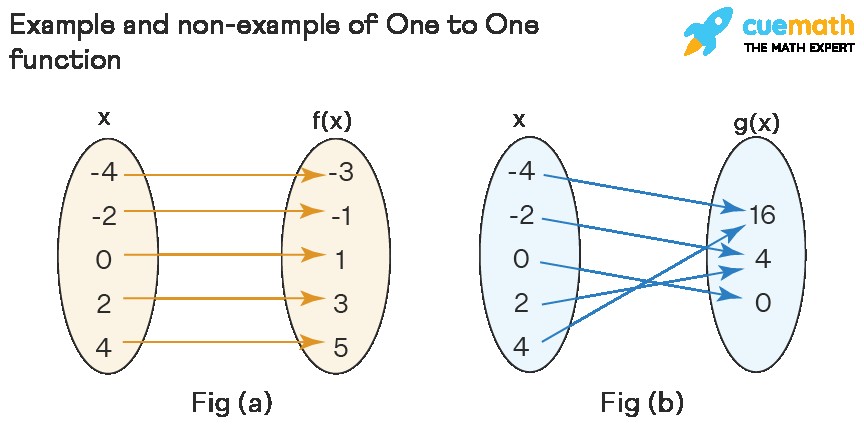
To visualize this, consider the following mappings:
In Figure (a), each value ( x ) in the domain maps to a unique value ( f(x) ) in the codomain, indicating a one to one function. In Figure (b), different values of ( x ) (e.g., 2 and -2) map to the same value of ( g(x) ) (4), showing that it is not a one to one function. This distinctive mapping characteristic is what sets one to one functions apart.
2. Horizontal Line Test
The horizontal line test is a visual method to determine if a function is one-to-one. It complements the algebraic approach by providing a graphical assessment.
- Draw a horizontal line across the graph of the function.
- If the horizontal line intersects the graph at more than one point, the function is not one-to-one.
- If the horizontal line never intersects the graph at more than one point, the function is one-to-one.
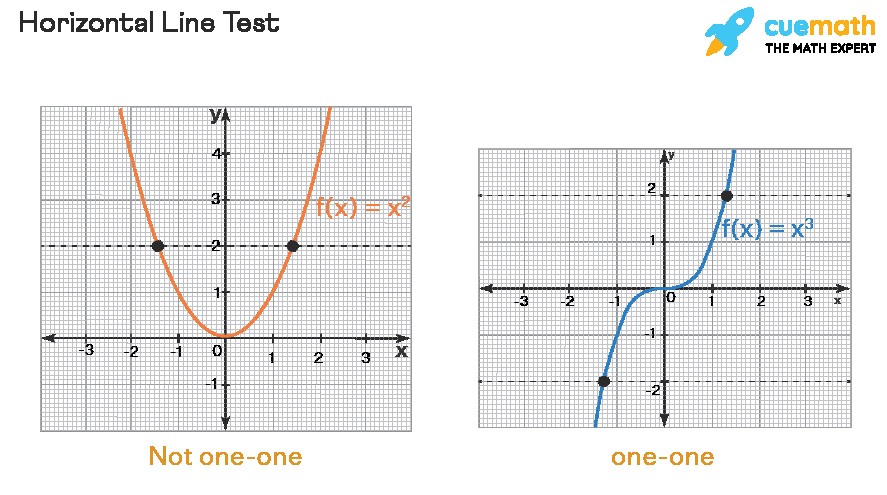
Example:
In the graph above, any horizontal line will intersect the curve at most once, indicating that the function passes the horizontal line test and is therefore a one to one function. This test provides a quick visual confirmation.
3. Properties of One to One Function
One-to-one functions, also known as injective functions, have unique characteristics that set them apart.
- Composition: If two functions, ( f(x) ) and ( k(x) ), are both one to one functions, then their composite function ( f circ k ) is also a one to one function. This can be shown as:
[
(f circ k)(x_1) = (f circ k)(x_2) Rightarrow f(k(x_1)) = f(k(x_2)) Rightarrow k(x_1) = k(x_2) Rightarrow x_1 = x_2
] - Domain and Range of Inverse: The domain of a function ( g ) is equal to the range of its inverse ( g^{-1} ), and the range of ( g ) is equal to the domain of ( g^{-1} ). This property highlights the symmetry between a function and its inverse.
- Monotonicity: A one to one function is either always increasing or always decreasing. This means that its graph will either consistently rise or fall as you move from left to right.
- Inverse Composition: ( g^{-1}(g(x)) = x ) for every ( x ) in the domain of ( g ), and ( g(g^{-1}(x)) = x ) for every ( x ) in the domain of ( g^{-1} ). This illustrates the inverse relationship where applying a function and then its inverse returns the original input.
- Injectivity of Composite: If ( f circ k ) is a one to one function, then ( k(x) ) is also guaranteed to be a one to one function.
- Symmetry of Graphs: The graph of a function and the graph of its inverse are symmetric with respect to the line ( y = x ). This symmetry is visually apparent when plotting both functions on the same coordinate plane.
These properties provide a deeper understanding of how one to one functions behave and how they relate to other mathematical concepts.
4. How to Determine if a Function is One to One?
Determining whether a function is one to one is crucial in many mathematical contexts. There are three primary methods to ascertain this: graphically, algebraically, and through the use of derivatives.
- Graphical Method (Horizontal Line Test): As previously mentioned, the horizontal line test involves drawing horizontal lines across the graph of the function. If any horizontal line intersects the graph more than once, the function is not one-to-one. This is a straightforward visual assessment.
- Algebraic Method: To prove a function ( g(x) ) is one to one algebraically, show that if ( g(a) = g(b) ), then ( a = b ) for all ( a ) and ( b ) in the domain of ( g ). This involves setting the function equal for two different inputs and demonstrating that those inputs must be equal.
- Using Derivatives: A function ( g(x) ) is one-to-one if its derivative ( g'(x) ) is either always positive (( g'(x) > 0 )) or always negative (( g'(x) < 0 )) throughout its domain. This means the function is either strictly increasing or strictly decreasing. For instance, the exponential function ( f(x) = e^x ) is strictly increasing over its entire domain (( -infty, infty )), hence it is one-to-one.
5. One to One Function Graph
A one to one function can be visually represented on a graph, where the domain is marked along the x-axis and the range along the y-axis. In a one to one function, no two points (( x_1, y_1 )) and (( x_2, y_2 )) share the same y-value. This means that no horizontal line will intersect the graph of the equation ( y = g(x) ) more than once.
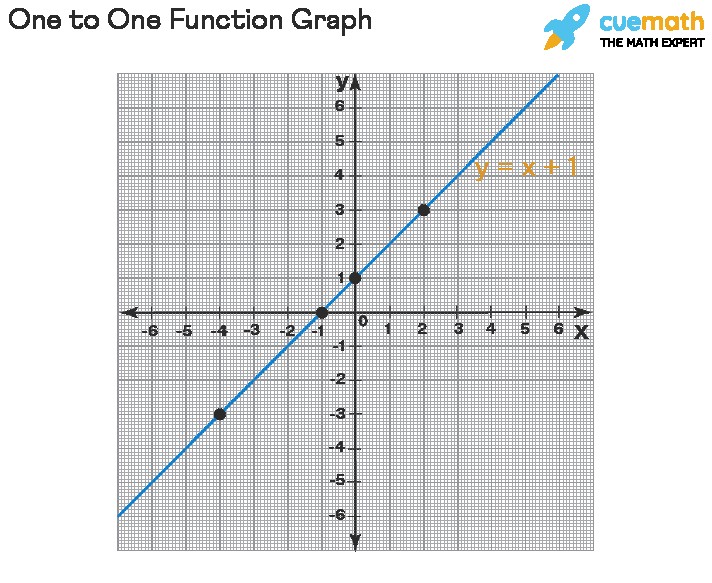
For example, the graph of the straight line ( y = x + 1 ) illustrates a one-to-one function:
Notice that no two points on this line have the same y-coordinate, confirming that it passes the horizontal line test and is indeed a one to one function.
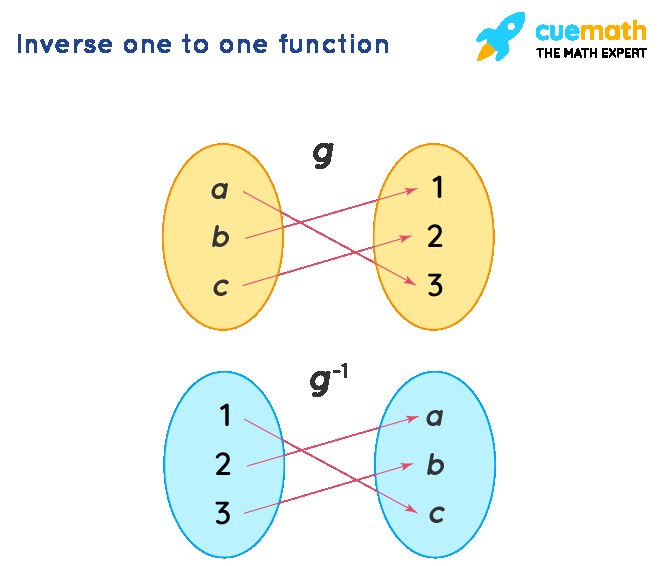
6. Inverse of One to One Function
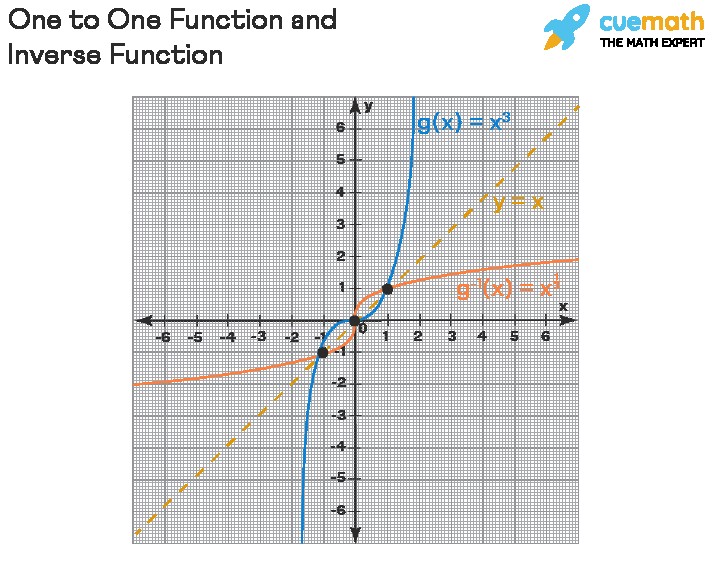
The concept of one-to-one functions is essential for understanding inverse functions. A function ( g ) has an inverse function, denoted as ( g^{-1} ), if and only if ( g ) is one-to-one. The inverse function ( g^{-1} ) essentially “undoes” the operation of ( g ).
In the illustration below, the ordered pairs of ( g^{-1} ) are obtained by swapping the coordinates in each ordered pair of ( g ). This means that the domain of ( g ) becomes the range of ( g^{-1} ), and the range of ( g ) becomes the domain of ( g^{-1} ).
6.1. Properties of the Inverse of One to One Function
The inverse of a one to one function has several important properties:
- A function ( f ) has an inverse function if and only if ( f ) is a one to one function.
- If ( g ) and ( f ) are inverses of each other, both functions are one to one functions.
- If ( f ) and ( g ) are inverses of each other, then ( (f circ g)(x) = x ) for ( x ) in the domain of ( g ), and ( (g circ f)(x) = x ) for ( x ) in the domain of ( f ).
- If ( f ) and ( g ) are inverses of each other, the domain of ( f ) equals the range of ( g ), and the range of ( f ) equals the domain of ( g ).
- The graphs of ( f ) and ( g ) (inverses of each other) are reflections of each other across the line ( y = x ).
- If the point ( (c, d) ) is on the graph of ( f ), then the point ( (d, c) ) is on the graph of ( f^{-1} ).
7. Steps to Find the Inverse of One to Function
To find the inverse function ( g^{-1}(x) ) for a one to one function ( g(x) ), follow these steps:
- Set ( g(x) ) equal to ( y ): ( y = g(x) ).
- Switch ( x ) and ( y ): ( x = g(y) ).
- Solve for ( y ) in terms of ( x ).
- Rename ( y ) as ( g^{-1}(x) ).
Example:
Find the inverse function ( g^{-1}(x) ) of the function ( g(x) = 3x – 2 ).
- Set ( g(x) = y ): ( y = 3x – 2 ).
- Switch ( x ) and ( y ): ( x = 3y – 2 ).
- Solve for ( y ):
[
x = 3y – 2
x + 2 = 3y
y = frac{x + 2}{3}
] - Rename ( y ) as ( g^{-1}(x) ):
[
g^{-1}(x) = frac{x + 2}{3}
]
Therefore, the inverse function of ( g(x) = 3x – 2 ) is ( g^{-1}(x) = frac{x + 2}{3} ).
Important Notes on One to One Function:
- One to one functions require equal numbers of items in the domain and range, ensuring each item is uniquely paired.
- Understanding one to one functions is essential for grasping inverse functions and solving certain equations.
- Determining if a function is one to one can be done both geometrically (horizontal line test) and algebraically.
8. FAQs on One to One Function
8.1. What is the Definition of One to One Function?
One to one functions, also known as injective functions, are defined as functions where each element of the range corresponds to a unique element in the domain. This means that for no two values ( x ) and ( y ) will ( f(x) ) equal ( f(y) ) unless ( x = y ). Unlike regular functions, one to one functions do not allow different input values to produce the same output.
8.2. What is the Difference Between Vertical Line Test and the Horizontal Line Test?
The vertical and horizontal line tests serve different purposes in determining the properties of a function.
| Vertical Line Test | Horizontal Line Test |
|---|---|
| Used to determine if a relation is a function. | Used to determine if a function is one-to-one. |
| If a vertical line does not meet the graph at more than one point, it is a function. | If a horizontal line does not meet the graph at more than one point, it is a one to one function. |
8.3. How Do You Check if a Function is One to One?
To check if a function is one to one, use either the graphical or algebraic method:
- Graphical Method: If the graph of the function passes the horizontal line test, it is considered a one to one function.
- Algebraic Method: Show that if ( g(x) = g(y) ), then ( x = y ) for all ( x ) and ( y ) in the domain.
8.4. What Types of Functions Are One to One Functions?
One to one functions are typically either strictly decreasing or strictly increasing.
- If ( f(x) ) is increasing, then ( f'(x) > 0 ) for every ( x ) in its domain.
- If ( f(x) ) is decreasing, then ( f'(x) < 0 ) for every ( x ) in its domain.
In essence, a one to one function ensures that different elements in the domain are never assigned the same value.
8.5. What Does It Mean if a Function is Not One to One Function?
If a function is not one-to-one, it means that a horizontal line can pass through the graph of the function more than once. Such functions are referred to as many-to-one functions, where different inputs can produce the same output.
8.6. What Are the Steps in Solving the Inverse of a One to One Function?
To solve for the inverse of a one to one function ( g(x) ):
- Replace ( g(x) ) with ( y ).
- Interchange the variables ( x ) and ( y ).
- Solve the equation for ( y ).
- Rename ( y ) as ( g^{-1}(x) ).
8.7. What is an Example of a One to One Function?
An example of a one to one function is ( f(x) = x + 3 ). This function produces a different output for each unique input ( x ). For example, ( f(1) = 4 ), ( f(2) = 5 ), and so on, with each element in the domain mapping to a unique element in the range.
8.8. What is Not a One to One Function?
The function ( f(x) = x^2 ) is not a one to one function because it produces the same output for different inputs. For instance, ( f(3) = 9 ) and ( f(-3) = 9 ), violating the condition for a function to be one to one.
8.9. Are Parabolas One to One Functions?
No, parabolas are generally not one to one functions. For example, the function ( g(y) = y^2 ) is a parabolic function where ( g(2) = 4 ) and ( g(-2) = 4 ). A horizontal line drawn through the parabola will intersect it twice, indicating that it is not a one to one function.
8.10. How Can We Apply the Concept of One to One Function in Daily Life?
One to one relationships are prevalent in everyday life. A common example is the relationship between a person and their social security number; each person has a unique number assigned only to them, illustrating a one-to-one correspondence.
Do you have more questions about one to one functions or other mathematical concepts? Visit WHAT.EDU.VN for free answers and expert assistance.
We understand that finding quick and reliable answers can be challenging. At WHAT.EDU.VN, we provide a platform where you can ask any question and receive accurate responses promptly.
Are you struggling to find solutions? Do you need information you can trust? Our services offer:
- A free platform to ask any question.
- Fast and accurate answers.
- Easy-to-understand explanations.
- A community to exchange knowledge.
- Free consultation for simple issues.
Don’t let your questions go unanswered. Visit WHAT.EDU.VN today and get the answers you need quickly and easily.
Contact us:
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: what.edu.vn