A buffer solution is a crucial component in many chemical and biological processes. It’s a solution designed to resist changes in pH when small amounts of acid or base are added. This stability is vital in reactions and processes that require a specific and consistent pH level. Understanding “What Is A Buffer” involves examining its composition and how it functions.
What is a Buffer Composed Of?
A buffer solution’s ability to maintain a stable pH stems from its unique composition. It must contain a weak conjugate acid-base pair. This can be achieved in one of two ways:
a. A weak acid and its conjugate base.
b. A weak base and its conjugate acid.
The choice between these two options depends on the desired pH of the buffer. Here are some examples of compounds that can function as buffers when combined in a solution:
-
Acetic acid (CH3COOH), a weak organic acid, and a salt containing its conjugate base, the acetate anion (CH3COO-), such as sodium acetate (CH3COONa).
-
Pyridine (C5H5N), a weak base, and a salt containing its conjugate acid, the pyridinium cation (C5H5NH+), such as Pyridinium Chloride.
-
Ammonia (NH3), a weak base, and a salt containing its conjugate acid, the ammonium cation (NH4+), such as Ammonium Hydroxide (NH4OH).
How Does a Buffer Work?
The effectiveness of a buffer lies in the equilibrium between the weak acid and its conjugate base. Both components are present in significant quantities and can neutralize small additions of acids (H3O+) or bases (OH-). Let’s consider the example of a Hydrofluoric Acid (HF) and Sodium Fluoride (NaF) buffer to illustrate this process.
Hydrofluoric acid is a weak acid because the fluoride ion (F-) has a strong attraction to protons (H3O+), hindering its complete dissociation in water. When HF is dissolved in water, it establishes the following equilibrium, with only slight dissociation (Ka(HF) = 6.6×10-4):
[HF_{(aq)} + H_2O_{(l)} rightleftharpoons F^-_{(aq)} + H_3O^+_{(aq)} nonumber ]
Sodium fluoride (NaF), when added to the solution, dissolves completely, yielding:
[NaF_{(aq)} + H_2O_{(l)} rightarrow Na^+_{(aq)} + F^-_{(aq)} nonumber ]
The sodium ion (Na+) is the conjugate of a strong base and does not affect the buffer’s pH. However, the addition of NaF increases the concentration of F- in the solution. According to Le Chatelier’s Principle, this increase in F- concentration will slightly suppress the dissociation of HF, further contributing to the buffering action. The presence of both HF and F- allows the solution to resist pH changes. This buffering action can be visualized using the titration curve of a buffer solution.
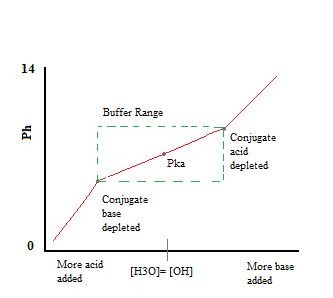Buffer titration curve showing the working range where pH changes are minimal
Alt text: Buffer titration curve illustrating minimal pH change within the working range, followed by rapid pH shift when the buffer capacity is exceeded.
The pH remains relatively stable within the buffer’s working range. Beyond this range, the pH changes drastically because the conjugate acid or base has been depleted through neutralization. A larger amount of conjugate acid or base leads to a greater buffering capacity.
If acid is added:
[F^-_{(aq)} + H_3O^+_{(aq)} rightleftharpoons HF_{(aq)} + H_2O_{(l)} nonumber ]
The conjugate base, F-, neutralizes the added acid (H3O+). This reaction proceeds to completion due to its large equilibrium constant (1/Ka(HF) = 1.5×10+3). As long as there is more F- than H3O+, almost all of the H3O+ will be consumed, shifting the equilibrium to the right. This slightly increases the concentration of HF and decreases the concentration of F-, resulting in minimal change in the overall H3O+ concentration.
If base is added:
[HF_{(aq)} + OH^-_{(aq)} rightleftharpoons F^-_{(aq)} + H_2O_{(l)} nonumber ]
The conjugate acid, HF, neutralizes the added base (OH-), again shifting the equilibrium to the right. This leads to a slight increase in F- concentration and a decrease in HF concentration. Since most of the OH- is neutralized, the pH change is minimal.
These reactions can alternate back and forth, maintaining a relatively stable pH.
Selecting Proper Components for Desired pH
Buffers are most effective when the pKa of the weak acid is close to the desired working pH range, which occurs when the concentrations of the conjugate acid and base are approximately equal.
For example, hydrofluoric acid has a Ka of 6.6 x 10-4, making its pKa approximately 3.18. Therefore, a hydrofluoric acid buffer is most effective around pH 3.18.
For the weak base ammonia (NH3), the Kb is 1.8×10-5. The Ka for its conjugate acid, NH4+, is Kw/Kb=10-14/1.8×10-5 = 5.6×10-10, resulting in a pKa of 9.25. Buffers using NH4+/NH3 work best around pH 9.25. The pKa of the conjugate acid dictates the approximate pH for a buffer system, and this is obviously dependent on the pKb of the conjugate base.
When the desired pH of a buffer solution is near the pKa of the conjugate acid being used, the Henderson-Hasselbalch equation provides a simple approximation of the solution’s pH.
Example 1: HF Buffer
To prepare an HF buffer at a pH of 3.0, we can use the Henderson-Hasselbalch approximation to determine the necessary ratio of F- and HF:
[pH = pKa + logdfrac{[Base]}{[Acid]} nonumber ]
[3.0 = 3.18 + logdfrac{[Base]}{[Acid]} nonumber ]
[logdfrac{[Base]}{[Acid]} = -0.18 nonumber ]
[dfrac{[Base]}{[Acid]} = 10^{-0.18} nonumber ]
[dfrac{[Base]}{[Acid]} = 0.66 nonumber ]
If we have 100 ml of 1 M HF and want to prepare a buffer using NaF, we need to calculate how much Sodium Fluoride to add.
We know that the ratio of base/acid should be 0.66. The molar mass of NaF is 41.99 g/mol. HF is a weak acid with a Ka = 6.6 x 10-4 and a concentration of 1 M.
The dissociation reaction is:
[HF_{(aq)} + H_2O_{(l)} rightleftharpoons F^-_{(aq)} + H_3O^+_{(aq)} nonumber ]
Since Ka is small, we can assume that virtually all HF remains undissociated, making the amount of F- from HF dissociation negligible. Thus, [HF] is approximately 1 M and [F-] is close to 0.
We want the ratio of Base/Acid to be 0.66, so [Base]/1M = 0.66. Thus, [F-] should be about 0.66 M. For 100 mL of solution, we will want to add 0.066 moles (0.1 L x 0.66 M) of F-. Since NaF completely dissociates in water, we need 0.066 moles of NaF, which is 0.066 moles x 41.99 g/mol = 2.767 g.
Note that because the conjugate acid and base are both mixed into the same volume of solution in the buffer, the ratio of “Base/Acid” can be determined using either a ratio of the concentrations or a ratio of the number of moles.
Adding Strong Acids or Bases to Buffer Solutions
Let’s explore what happens when we add a strong acid like HCl to our F-/HF buffer. We have 0.066 moles of F- and 0.10 moles of HF. The pH can be verified using the Henderson-Hasselbalch Approximation:
pH = pKa + log(Base/Acid) = 3.18 + log(0.066 moles F-/0.10 moles HF) = 3.00
When HCl is added to water, it completely dissociates into H3O+ and Cl-. The Cl- is inert, but the H3O+ affects pH and reacts with the buffer components:
[F^-_{(aq)} + H_3O^+_{(aq)} rightleftharpoons HF_{(aq)} + H_2O_{(l)} nonumber ]
For every mole of H3O+ added, an equivalent amount of F- reacts. If the F- is used up before the H3O+, the buffer capacity is exceeded. If we add 0.01 moles of HCl to this system, the H3O+ will all be consumed by the reaction with F-.
The 0.066 moles of F- is reduced by the amount of H30+ added:
- 066 initial moles F- – 0.010 moles reacted with H3O+ = 0.056 moles F- remaining
During this process, more HF is formed:
- 10 initial moles HF + 0.010 moles from reaction of F- with H3O+ = 0.11 moles HF after reaction
Plugging these new values into Henderson-Hasselbalch gives:
pH = pKa + log (base/acid) = 3.18 + log (0.056 moles F-/0.11 moles HF) = 2.89
The buffer resisted the change in pH, only dropping from 3.00 to 2.89 with the addition of 0.01 moles of strong acid.
References
- Brown, et al. Chemistry:The Central Science. 11th ed. Upper Saddle River, New Jersey: Pearson/Prentice Hall, 2008.
- Chang, Raymond. General Chemistry:The Essential Concepts. 3rd ed. New York: Mcgraw Hill, 2003
- Petrucci, et al. General Chemistry: Principles & Modern Applications. 9th ed. Upper Saddle River, New Jersey: Pearson/Prentice Hall, 2007.
Outside Links
- Urbansky, Edward T.; Schock, Michael R. “Understanding, Deriving, and Computing Buffer Capacity.” J. Chem. Educ. 2000 1640..
