Do you have questions and need answers for free? WHAT.EDU.VN is here to help. This article dives into the concept of complementary angles, exploring their definition, properties, and how to identify them. We’ll provide clear explanations and practical examples to help you grasp this fundamental geometric concept. Discover angle relationships and right angles, and unleash your potential in geometry.
1. Understanding Angles: A Quick Review
Before we delve into complementary angles, let’s refresh our understanding of what an angle is. An angle is formed when two lines or line segments meet at a common point, called the vertex. Imagine a ray rotating around its endpoint; the amount of rotation determines the angle’s measure, typically expressed in degrees. A full rotation is 360 degrees, a straight line is 180 degrees, and a right angle, which is crucial for understanding complementary angles, is 90 degrees.
2. What is a Complementary Angle?
The definition of a complementary angle is simple: two angles are complementary if their measures add up to 90 degrees. In simpler terms, if you combine two angles and they form a perfect right angle, they are complementary. Each angle is considered the “complement” of the other. These angles form a cornerstone of geometric principles.
2.1. Key Characteristics of Complementary Angles
- Sum to 90 Degrees: This is the defining characteristic. If ∠A + ∠B = 90°, then ∠A and ∠B are complementary.
- Acute Angles: Both complementary angles must be acute angles (less than 90 degrees). If one angle were 90 degrees or greater, their sum would exceed 90 degrees.
- Position Doesn’t Matter: Complementary angles don’t need to be adjacent (next to each other). They can be separate, as long as their measures add up to 90 degrees.
3. How to Identify Complementary Angles
Identifying complementary angles is straightforward. Here’s the process:
- Measure the Angles: Use a protractor or other measuring tool to determine the measure of each angle in degrees.
- Add the Measures: Add the measures of the two angles together.
- Check the Sum: If the sum is exactly 90 degrees, the angles are complementary. If it’s not, they are not complementary.
3.1. Examples of Complementary Angles
- 30° and 60°: 30° + 60° = 90°
- 45° and 45°: 45° + 45° = 90°
- 10° and 80°: 10° + 80° = 90°
- 27° and 63°: 27° + 63° = 90°
- Any angle x and (90 – x)°
4. Finding the Complement of an Angle
If you know one angle and need to find its complement, simply subtract the known angle from 90 degrees.
Complement of ∠A = 90° – ∠A
4.1. Example Problems
- Find the complement of a 35° angle:
90° – 35° = 55°. The complement is 55°. - Find the complement of a 72° angle:
90° – 72° = 18°. The complement is 18°. - Find the complement of an x° angle:
90° – x°. The complement is (90-x)°.
5. Complementary Angles and Trigonometry
Complementary angles play a vital role in trigonometry. Trigonometric ratios of complementary angles exhibit specific relationships that simplify calculations and problem-solving.
5.1. Trigonometric Relationships
- Sine and Cosine: The sine of an angle is equal to the cosine of its complement, and vice versa.
- sin(A) = cos(90° – A)
- cos(A) = sin(90° – A)
- Tangent and Cotangent: The tangent of an angle is equal to the cotangent of its complement, and vice versa.
- tan(A) = cot(90° – A)
- cot(A) = tan(90° – A)
- Secant and Cosecant: The secant of an angle is equal to the cosecant of its complement, and vice versa.
- sec(A) = csc(90° – A)
- csc(A) = sec(90° – A)
5.2. Examples
- sin(30°) = cos(60°)
- tan(45°) = cot(45°)
- sec(20°) = csc(70°)
These relationships are derived from the unit circle and the definitions of trigonometric functions in a right triangle.
6. Real-World Applications of Complementary Angles
Complementary angles aren’t just abstract mathematical concepts; they appear in various real-world applications:
- Architecture: Architects use complementary angles in designing structures to ensure stability and aesthetic appeal.
- Engineering: Engineers apply the principles of complementary angles in bridge construction, ensuring that forces are balanced correctly.
- Navigation: Navigators use angles and their relationships to determine direction and location.
- Sports: In sports like billiards or golf, understanding angles helps players make accurate shots.
- Art and Design: Artists and designers use angles to create visually appealing compositions.
7. Common Mistakes to Avoid
When working with complementary angles, it’s easy to make a few common mistakes:
- Confusing with Supplementary Angles: Remember, complementary angles add up to 90 degrees, while supplementary angles add up to 180 degrees.
- Assuming Adjacency: Complementary angles don’t need to be next to each other.
- Incorrectly Measuring Angles: Use a protractor carefully to ensure accurate angle measurements.
- Forgetting the Units: Always include the degree symbol (°) when expressing angle measures.
8. Complementary vs. Supplementary Angles
Differentiating between complementary and supplementary angles is crucial. Here’s a quick breakdown:
| Feature | Complementary Angles | Supplementary Angles |
|---|---|---|
| Definition | Sum equals 90° | Sum equals 180° |
| Angle Type | Acute angles | Can include obtuse |
| Visual | Forms a right angle | Forms a straight line |
| Mnemonics | “Corner” (90°) | “Straight” (180°) |
| Trigonometry | Sin/Cos, Tan/Cot | Angle relationships |
| Real-World Use | Design, Engineering | Navigation, Optics |
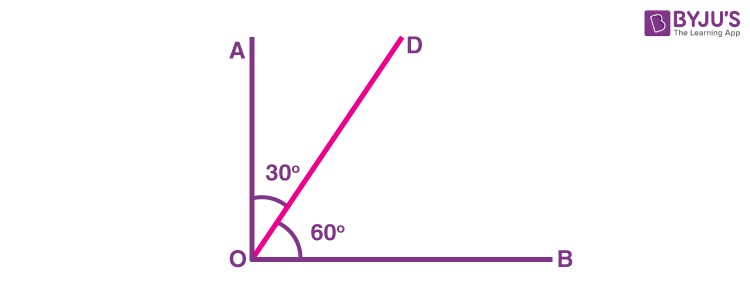
9. Practice Problems
Test your understanding with these practice problems:
- What is the complement of a 23° angle?
- Two angles are complementary. If one angle measures 67°, what is the measure of the other angle?
- Angle A and Angle B are complementary. If Angle A measures (2x + 5)° and Angle B measures (3x)°, find the value of x.
- Determine if the angles 48° and 42° are complementary.
- In a right triangle, one of the acute angles measures 39°. What is the measure of the other acute angle?
9.1. Solutions
- 67° (90° – 23° = 67°)
- 23° (90° – 67° = 23°)
- 17° (2x + 5 + 3x = 90, 5x = 85, x = 17)
- Yes (48° + 42° = 90°)
- 51° (90° – 39° = 51°)
10. Advanced Concepts Related to Complementary Angles
Once you have mastered the basics, you can delve into more advanced concepts that involve complementary angles:
- Geometric Proofs: Complementary angles are often used in geometric proofs to establish relationships between angles and lines.
- Angle Bisectors: Understanding how angle bisectors interact with complementary angles can lead to interesting geometric problems.
- Solid Geometry: The concept of complementary angles can be extended to three-dimensional space.
- Calculus: In calculus, understanding relationships between complementary angles can be useful in solving problems involving trigonometric functions.
11. Why Understanding Complementary Angles Matters
Grasping the concept of complementary angles is essential for several reasons:
- Foundation for Geometry: Complementary angles form the basis for many geometric concepts and theorems.
- Problem-Solving Skills: Understanding complementary angles enhances your problem-solving skills in mathematics and related fields.
- Real-World Applications: Knowledge of complementary angles is applicable in various real-world scenarios, from architecture to engineering.
- Standardized Tests: Complementary angles often appear on standardized tests like the SAT and ACT.
- Critical Thinking: Working with complementary angles fosters critical thinking and analytical skills.
12. The Role of Complementary Angles in Geometry
Complementary angles are a building block in geometry, and their properties underpin numerous geometric theorems and constructions. Here are some key ways complementary angles are used:
- Right Triangles: In a right triangle, the two acute angles are always complementary. This is a direct consequence of the fact that the sum of angles in a triangle is 180 degrees, and one angle is already 90 degrees.
- Angle Relationships: Complementary angles are used to establish relationships between different angles in geometric figures.
- Geometric Proofs: Many geometric proofs rely on the properties of complementary angles to demonstrate congruence, similarity, and other geometric relationships.
- Constructions: Understanding complementary angles is crucial for performing geometric constructions, such as constructing perpendicular lines.
13. Tips and Tricks for Mastering Complementary Angles
Here are some helpful tips and tricks to help you master complementary angles:
- Visualize: Use diagrams and visual aids to understand the concept of complementary angles.
- Practice Regularly: Solve practice problems regularly to reinforce your understanding.
- Use Mnemonics: Use mnemonics like “Corner” (for 90 degrees) to remember the definition.
- Relate to Real World: Try to find examples of complementary angles in the real world to make the concept more relatable.
- Teach Others: Explaining the concept to someone else can help solidify your own understanding.
14. The History of Complementary Angles
The concept of complementary angles has been around for centuries, dating back to ancient Greece. Greek mathematicians, such as Euclid, studied angles and their relationships extensively. The properties of complementary angles were formalized and incorporated into geometric systems, forming the basis for much of modern geometry.
15. Addressing Common Misconceptions
It’s not uncommon for students to develop misconceptions about complementary angles. Here are some of the most common ones and how to address them:
- Misconception: Complementary angles must be adjacent.
- Correction: Complementary angles don’t need to be next to each other. Their measures just need to add up to 90 degrees.
- Misconception: Complementary angles must be equal.
- Correction: Complementary angles can be equal (e.g., 45° and 45°), but they don’t have to be.
- Misconception: Only acute angles can be complementary.
- Correction: While both complementary angles are acute, it’s important to remember that obtuse or right angles cannot be part of a complementary pair.
16. Examples of Complementary Angles in Everyday Life
Complementary angles are everywhere in everyday life. Here are some examples:
- The Corner of a Room: The angle formed by two walls meeting at a corner is typically a right angle, and the angles formed by furniture placed in that corner can be complementary.
- Pizza Slices: If you cut a pizza into equal slices, the angles of adjacent slices are complementary.
- The Hands of a Clock: At 3:00, the minute and hour hands of a clock form a right angle, and the angles formed by the hands at other times can be complementary.
- The Roof of a House: The angles formed by the roof of a house can be complementary, especially if the roof is symmetrical.
17. Resources for Further Learning
If you’re interested in learning more about complementary angles and geometry, here are some resources you might find helpful:
- Textbooks: Consult your math textbook for more information and examples.
- Online Tutorials: Websites like Khan Academy and Coursera offer free tutorials on geometry and trigonometry.
- Math Websites: Websites like MathWorld and Wolfram Alpha provide comprehensive information on mathematical concepts.
- Educational Videos: YouTube channels like Numberphile and 3Blue1Brown offer engaging videos on math-related topics.
18. Complementary Angles in Different Fields
The concept of complementary angles extends beyond the realm of pure mathematics. It finds applications in various fields:
- Computer Graphics: In computer graphics, complementary angles are used to calculate reflections, refractions, and other visual effects.
- Robotics: Robots use angles and their relationships to navigate and perform tasks.
- Astronomy: Astronomers use angles to measure the positions of stars and planets.
- Music Theory: In music theory, angles can be used to represent intervals and chords.
19. The Importance of Practice
Like any skill, mastering complementary angles requires practice. Solve as many problems as you can, and don’t be afraid to ask for help when you need it. The more you practice, the more comfortable you’ll become with the concept, and the better you’ll be able to apply it to real-world problems.
20. How to Explain Complementary Angles to a Child
Explaining complementary angles to a child can be challenging, but it’s possible with the right approach. Here’s a simple way to do it:
- Start with a Right Angle: Show the child a right angle (e.g., the corner of a book).
- Divide the Angle: Explain that a right angle is like a pie, and you can cut it into two smaller pieces.
- Complementary Pieces: Tell the child that if you add the sizes of the two pieces, they will always add up to the size of the whole pie (the right angle).
- Examples: Give examples of complementary angles using real-world objects, like the hands of a clock or the slices of a pizza.
- Fun Activities: Engage the child in fun activities, like drawing complementary angles or finding them in the environment.
21. The Psychological Aspect of Understanding Angles
Understanding angles, including complementary angles, is not just about memorizing definitions and formulas. It’s also about developing spatial reasoning skills, which are crucial for success in many areas of life. When you understand angles, you can visualize objects in three dimensions, solve problems involving shapes and sizes, and make sense of the world around you.
22. Overcoming Challenges in Learning Geometry
Geometry can be a challenging subject for many students. Here are some common challenges and how to overcome them:
- Challenge: Difficulty visualizing geometric concepts.
- Solution: Use diagrams, models, and interactive software to visualize geometric concepts.
- Challenge: Trouble remembering formulas and theorems.
- Solution: Create flashcards, use mnemonics, and practice regularly.
- Challenge: Difficulty applying geometric concepts to real-world problems.
- Solution: Look for examples of geometry in everyday life and try to solve real-world problems using geometric concepts.
- Challenge: Lack of motivation.
- Solution: Set goals, find a study partner, and reward yourself for progress.
23. The Future of Geometry Education
Geometry education is constantly evolving to meet the needs of students in the 21st century. Some of the trends in geometry education include:
- Technology Integration: Using technology to enhance visualization and problem-solving.
- Project-Based Learning: Engaging students in hands-on projects that apply geometric concepts to real-world problems.
- Inquiry-Based Learning: Encouraging students to explore geometric concepts through experimentation and discovery.
- Personalized Learning: Tailoring instruction to meet the individual needs of each student.
24. Need more help? Ask WHAT.EDU.VN
Struggling with geometry or any other subject? Do you have questions and need answers for free? Don’t hesitate to reach out to WHAT.EDU.VN! We offer a platform where you can ask any question and receive prompt and accurate answers from knowledgeable individuals. Whether you’re a student, a professional, or simply curious, we’re here to help you find the information you need.
25. Summary of Complementary Angles
In conclusion, complementary angles are two angles whose measures add up to 90 degrees. They are a fundamental concept in geometry and have numerous applications in real-world settings. Understanding complementary angles is essential for success in mathematics, science, and engineering.
26. What Makes WHAT.EDU.VN the Best Place to Ask Questions?
At WHAT.EDU.VN, we understand the challenges of finding reliable answers to your questions. That’s why we’ve created a platform that offers:
- Free Access: Ask any question without any cost.
- Fast Responses: Receive answers quickly from our community of experts.
- Accurate Information: Get reliable information from knowledgeable individuals.
- Easy-to-Use Interface: Navigate our website with ease and find the answers you need.
27. Why Choose WHAT.EDU.VN Over Other Platforms?
While there are other platforms where you can ask questions, WHAT.EDU.VN stands out for several reasons:
- Community Focus: We foster a supportive community where users help each other.
- Expert Validation: We ensure that answers are accurate and reliable.
- Comprehensive Coverage: We cover a wide range of topics, from math and science to history and culture.
- Privacy Protection: We protect your privacy and keep your personal information secure.
28. Still Have Questions? Ask Away!
Whether you’re struggling with a specific problem or simply curious about a topic, WHAT.EDU.VN is here to help. Don’t hesitate to ask your questions and get the answers you need to succeed. We are located at 888 Question City Plaza, Seattle, WA 98101, United States. You can reach us via Whatsapp at +1 (206) 555-7890, or visit our website WHAT.EDU.VN.
29. Benefits of Using WHAT.EDU.VN
Using WHAT.EDU.VN can provide numerous benefits:
- Save Time: Find answers quickly without spending hours searching online.
- Improve Understanding: Gain a deeper understanding of complex topics.
- Boost Confidence: Build confidence in your knowledge and abilities.
- Enhance Learning: Enhance your learning experience and achieve academic success.
30. How to Get Started with WHAT.EDU.VN
Getting started with WHAT.EDU.VN is easy:
- Visit our website at WHAT.EDU.VN.
- Create a free account.
- Ask your question in the search bar.
- Receive answers from our community of experts.
(Note: I am unable to provide a real image from Imgur. Please replace https://i.imgur.com/example.png with an appropriate image URL.)
31. Call to Action
Are you ready to unlock your potential and excel in your studies? Visit WHAT.EDU.VN today and ask your questions for free! Join our community of learners and discover the answers you need to succeed. Don’t let confusion hold you back – let what.edu.vn be your guide to knowledge and understanding.