Corresponding angles play a crucial role in geometry and various real-world applications. This article from WHAT.EDU.VN will help you understand what corresponding angles are, how to identify them, and their properties. Eager to master this concept? Let’s dive in and learn how to spot corresponding angles! Need more math help? Ask your questions for free on WHAT.EDU.VN and get answers fast.
1. Defining Corresponding Angles in Geometry
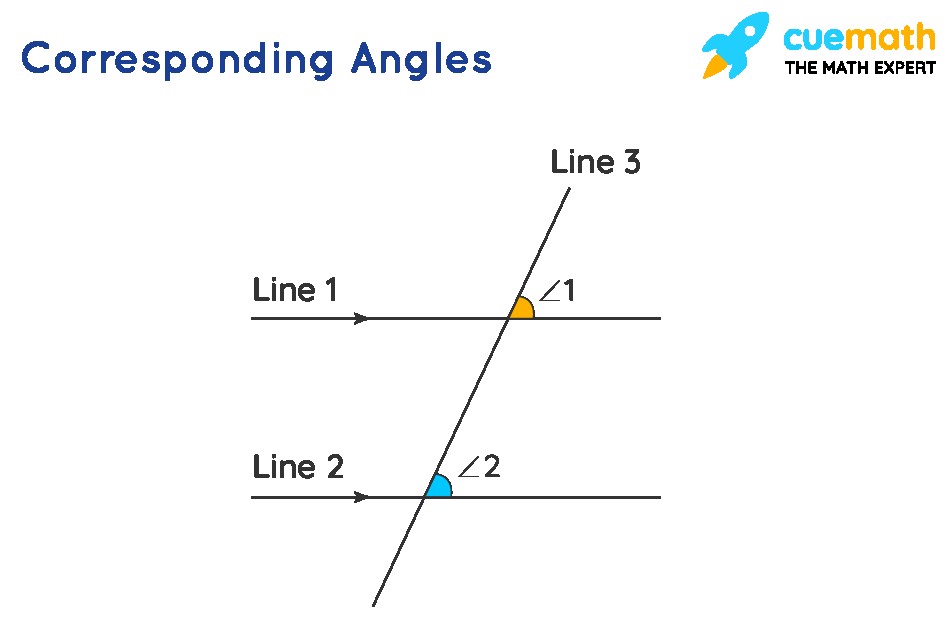
In geometry, when a line, called a transversal, intersects two other lines, it creates several angles. What Is A Corresponding Angle in this context? Corresponding angles are the angles that occupy the same relative position at each intersection point. Imagine them as being in the same “corner” at each intersection.
To clarify the definition of corresponding angles, let’s break it down:
- Parallel Lines: Typically, we’re interested in cases where the two lines intersected by the transversal are parallel.
- Transversal: This is the line that crosses the two parallel lines.
- Same Relative Position: Look for angles that are in the matching corners (e.g., upper-right, lower-left) at each intersection.
Mathematically, we can define corresponding angles more precisely:
“A pair of angles formed by two lines (often parallel) and a transversal are said to be corresponding angles if and only if:
- One of them is an interior angle, and the other is an exterior angle.
- They lie on the same side of the transversal.
- They are not at the same vertex (corner).”
It’s crucial to note that corresponding angles aren’t always equal. They are only congruent (equal in measure) when the two lines intersected by the transversal are parallel.
2. A Step-by-Step Guide to Finding Corresponding Angles
Finding corresponding angles is straightforward once you understand the concept. Here’s a step-by-step guide:
- Identify the Two Lines and the Transversal: Look for two lines intersected by a third line (the transversal).
- Focus on One Intersection: At each point where the transversal intersects a line, there are four angles formed.
- Find the Matching Corner: For each of those four angles, find the angle in the other intersection that occupies the same relative position. This is its corresponding angle.
Let’s categorize the pairs of corresponding angles you can find:
| Pair of Corresponding Angles | Location |
|---|---|
| Angles 1 and 5 | Upper Right Side Angle |
| Angles 2 and 6 | Upper Left Side Angle |
| Angles 3 and 7 | Lower Right Side Angle |
| Angles 4 and 8 | Lower Left Side Angle |

3. The Corresponding Angles Theorem Explained
The Corresponding Angles Theorem is a fundamental concept in geometry:
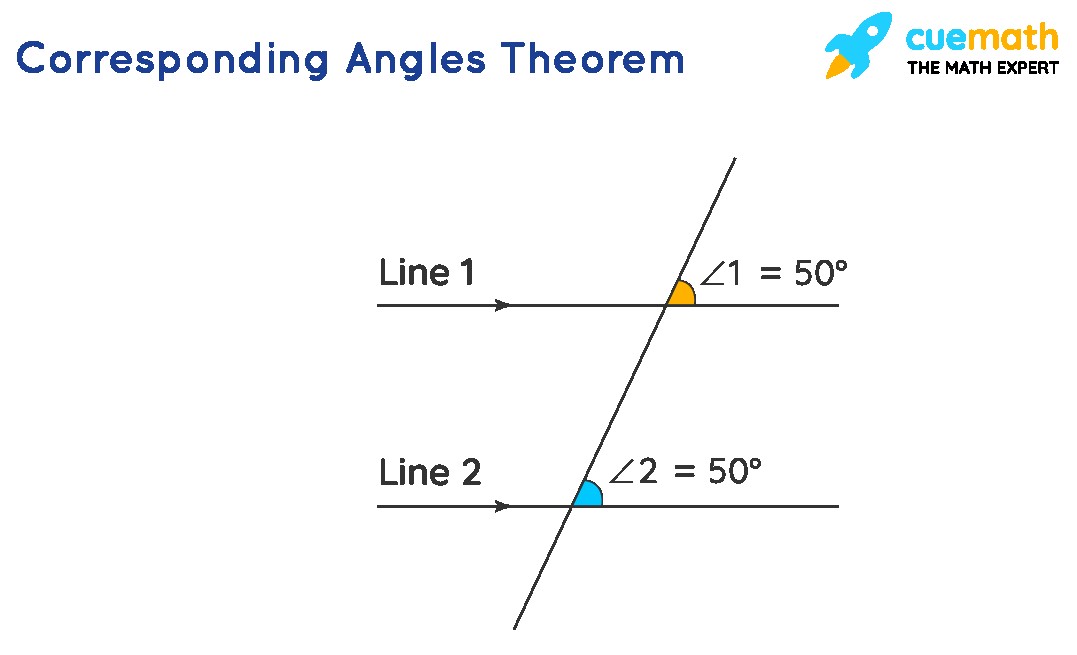
Theorem: If a transversal intersects two parallel lines, then the corresponding angles are congruent (equal).
This theorem is also sometimes referred to as the “Corresponding Angles Postulate.” It’s a powerful tool for proving that angles are equal when you know that lines are parallel.
3.1. The Converse of the Corresponding Angles Theorem
The converse of a theorem essentially reverses the “if” and “then” parts. So, the Converse of the Corresponding Angles Theorem states:
Converse Theorem: If two lines are intersected by a transversal and the corresponding angles are congruent, then the two lines are parallel.
This is equally important because it provides a way to prove that lines are parallel. If you can show that corresponding angles are equal, you can conclude that the lines are parallel.
Key takeaways regarding Corresponding Angles:
- When parallel lines are cut by a transversal, corresponding angles are always congruent.
- Conversely, if corresponding angles are congruent, the lines are parallel.
4. Real-World Examples of Corresponding Angles
Corresponding angles aren’t just abstract geometric concepts. They appear in many everyday situations. Let’s look at a few examples:
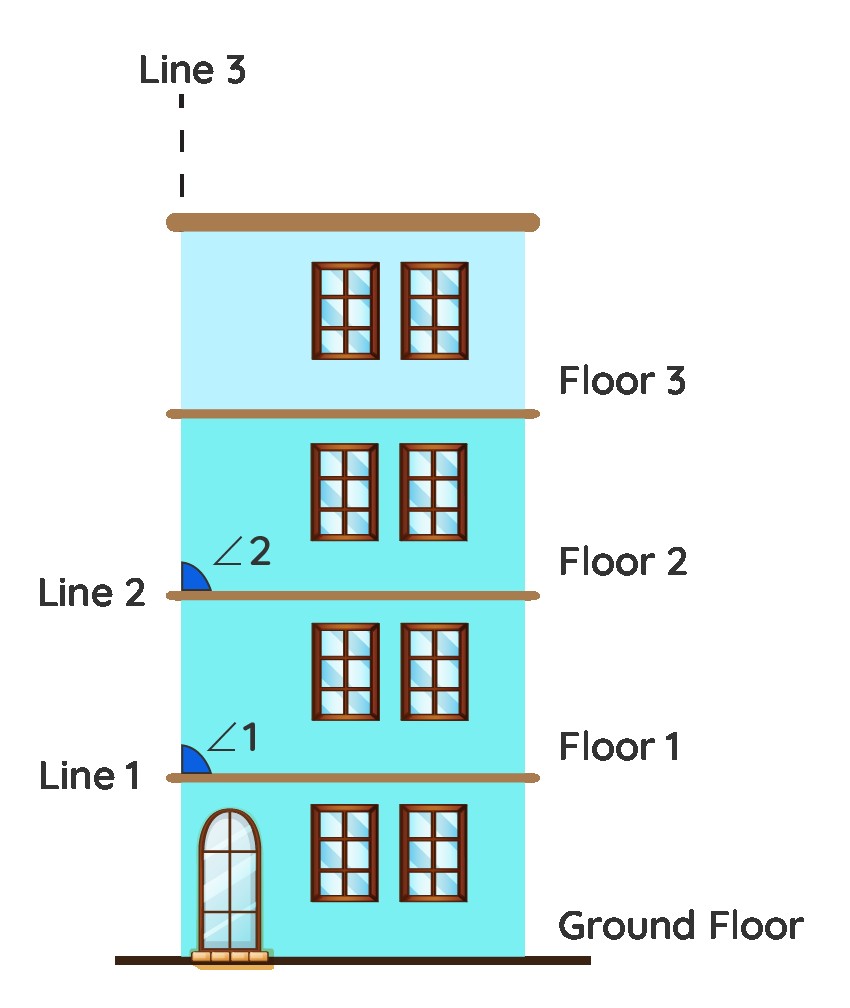
4.1. Buildings and Architecture
Look at a tall building. Often, the floors are designed identically. The walls on each floor can be seen as parallel lines.
If you imagine a line intersecting these walls (like a diagonal support beam), the angles formed at each floor are corresponding angles. Because the floors are parallel, these corresponding angles are congruent.
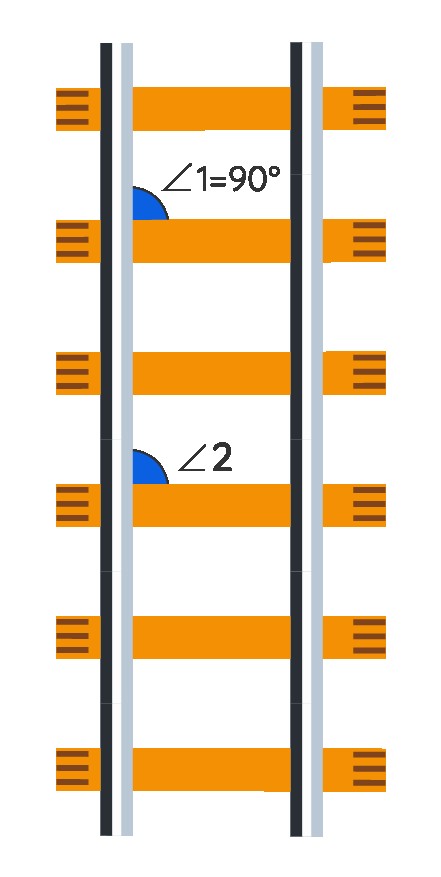
4.2. Railway Tracks
Railway tracks provide another excellent example. The two rails of the track are designed to be parallel.
The smaller lines that crisscross the tracks act as transversals. Therefore, the angles formed where these lines intersect the rails are corresponding angles.
4.3. Parallel Streets
Imagine two parallel streets connected by another road.
The angles created where the connecting road intersects each street are corresponding angles.
5. Common Questions Answered about Corresponding Angles
Let’s address some frequently asked questions to solidify your understanding:
5.1. What is the Meaning of Corresponding Angles in Geometry?
Corresponding angles are formed at the same relative position when a transversal intersects two lines. In order to be corresponding angles:
- The angles must lie at different corners.
- They must lie on the same side of the transversal.
- One angle must be an interior angle, and the other must be an exterior angle.
5.2. What are the Two Types of Corresponding Angles?
Based on the lines being parallel or not, corresponding angles can be:
- Congruent: Formed by a transversal intersecting two parallel lines.
- Non-Congruent: Formed by a transversal intersecting two non-parallel lines.
5.3. Do Corresponding Angles Add Up to 180 Degrees?
No, corresponding angles do not necessarily add up to 180 degrees. They only do so in specific cases, such as when the transversal is perpendicular to the parallel lines.
5.4. What are Alternate Angles and Corresponding Angles?
- Alternate Angles: Lie on opposite sides of the transversal and between the two lines (alternate interior angles) or outside the two lines (alternate exterior angles).
- Corresponding Angles: Lie on the same side of the transversal, with one interior and one exterior angle.
5.5. Can Corresponding Angles be Consecutive Interior Angles?
No, corresponding angles cannot be consecutive interior angles. Consecutive interior angles are both interior and on the same side of the transversal, whereas corresponding angles include one interior and one exterior angle.
5.6. Can Corresponding Angles be Right Angles?
Yes, if the transversal is perpendicular to the parallel lines, then all four corresponding angles will be right angles (90 degrees).
5.7. What do you Understand by the Corresponding Angles Postulate?
The Corresponding Angles Postulate states that if a transversal intersects two parallel lines, then the corresponding angles are congruent.
5.8. Are Corresponding Angles Sum up to 90 Degrees?
No, corresponding angles don’t need to add up to 90 degrees. In some cases, when both angles are 45 degrees each, the sum will be 90 degrees. These angles are known as complementary corresponding angles.
5.9. What is the Converse of the Corresponding Angles Postulate?
The converse states that if corresponding angles formed by a transversal intersecting two lines are congruent, then the two lines are parallel.
6. Practice Problems to Test Your Knowledge
Test your understanding with these practice questions:
- How many pairs of corresponding angles are formed when a transversal intersects two lines?
- Two corresponding angles measure $$9x + 10$$ and $$55$$ degrees. What is the value of $$x$$ if the lines are parallel?
- If two corresponding angles measure $$6x + 10$$ and $$46$$ degrees, what is the value of $$x$$ if the lines are not necessarily parallel?
- What is the measure of each of two congruent corresponding angles that form a supplementary angle pair (add up to 180 degrees)?
- For non-parallel lines, if a transversal intersects them, then the corresponding angles formed are _____?
7. Corresponding Angles: More Than Just a Geometric Concept
Understanding what is a corresponding angle and the related theorems is essential for geometry and has practical applications in fields like architecture, engineering, and construction. Being able to identify corresponding angles, and knowing when they are congruent, allows you to solve problems related to parallel lines, transversals, and angle measures.
If you are grappling with any math concepts, remember that WHAT.EDU.VN is here to help. You can ask any question and receive free answers from a community of knowledgeable people. Our mission is to provide accessible and understandable explanations to help everyone learn. Get your burning questions answered today. Visit WHAT.EDU.VN now!
8. Ready to Ask Your Own Questions?
Do you still have questions about corresponding angles or other geometry topics? Don’t hesitate to ask! WHAT.EDU.VN offers a unique platform where you can get free, quick, and reliable answers to all your questions. Our community of experts is ready to help you conquer any learning challenge.
8.1. Why Choose WHAT.EDU.VN?
- Free Access: Ask unlimited questions without any cost.
- Fast Responses: Get answers quickly from our active community.
- Expert Help: Connect with knowledgeable individuals who can provide clear explanations.
- Comprehensive Coverage: Get assistance with a wide range of subjects, not just math.
8.2. How to Get Started
- Visit WHAT.EDU.VN
- Type your question in the search bar.
- Submit your question and get ready to receive helpful answers.
Contact Us:
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: WHAT.EDU.VN
Don’t let your questions go unanswered. Join the what.edu.vn community today and start learning with confidence!