What Is A Diameter? It’s a fundamental concept in geometry, deeply connected to circles and their properties. WHAT.EDU.VN offers a clear understanding of this concept, providing insights into its definition, calculation, and applications. Discover the secrets of the diameter and unlock a new level of mathematical understanding. Let’s explore circles, radii, and more!
1. Understanding the Diameter of a Circle
The diameter of a circle is a straight line segment that passes through the center of the circle, with both endpoints lying on the circle’s circumference. It’s essentially the longest possible chord within a circle. Think of it as cutting the circle perfectly in half.
1.1. Definition Explained
The diameter is defined as twice the length of the radius of a circle. In simpler terms, if you draw a line from the center of the circle to any point on its edge (that’s the radius), the diameter is simply that length doubled. The diameter always passes through the center of the circle, dividing it into two equal halves.
1.2. The Diameter Symbol (Ø)
In engineering drawings and technical specifications, the symbol “Ø” is commonly used to represent the diameter. For instance, “Ø50 mm” indicates that the circle’s diameter is 50 millimeters. This symbol helps avoid confusion and clearly communicates the size of circular components.
2. Diameter of Circle Formulas: Your Toolkit
Understanding the formulas for calculating the diameter of a circle is crucial. There are several ways to determine the diameter, depending on the information you have available.
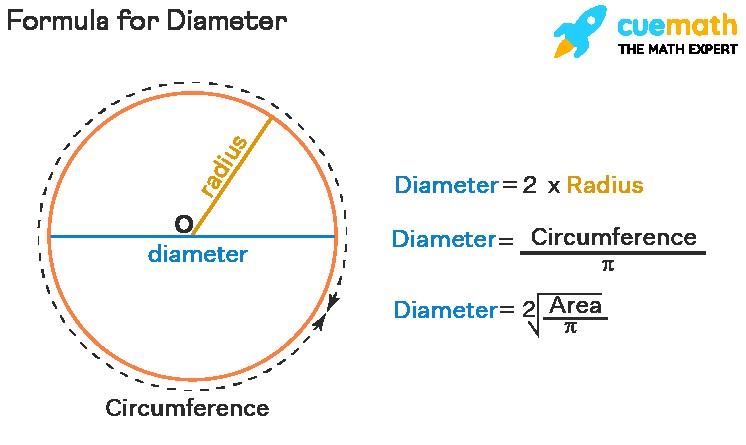Diameter formula
2.1. Using the Circumference
The circumference of a circle is the distance around it. The relationship between the circumference (C) and the diameter (d) is defined by the formula: C = πd, where π (pi) is a mathematical constant approximately equal to 3.14159.
To find the diameter using the circumference, rearrange the formula:
Diameter = Circumference / π
2.2. Using the Radius
The radius (r) is the distance from the center of the circle to any point on its circumference. The diameter is simply twice the radius:
*Diameter = 2 Radius**
This is perhaps the most straightforward way to calculate the diameter if you know the radius.
2.3. Using the Area
If you know the area (A) of the circle, you can also find the diameter. The formula for the area of a circle is: A = πr².
First, solve for the radius:
r = √(A / π)
Then, calculate the diameter:
*Diameter = 2 √(A / π)**
3. Step-by-Step: Finding the Diameter
Let’s break down the process of finding the diameter with clear, actionable steps:
-
Step 1: Identify the known information. Do you know the radius, circumference, or area?
-
Step 2: Choose the appropriate formula based on the available information (as outlined in Section 2).
-
Step 3: Substitute the known values into the formula and solve for the diameter.
-
Step 4: Double-check your answer to ensure it makes sense within the context of the problem.
Example: A circle has a circumference of 25 cm. Find its diameter.
- Step 1: Known information: Circumference (C) = 25 cm
- Step 2: Formula: Diameter = Circumference / π
- Step 3: Calculation: Diameter = 25 cm / 3.14159 ≈ 7.96 cm
Therefore, the diameter of the circle is approximately 7.96 cm.
4. Diameter vs. Radius: Key Differences
While closely related, the diameter and radius are distinct concepts. Understanding their differences is crucial for grasping circle geometry.
| Feature | Diameter | Radius |
|---|---|---|
| Definition | A line segment passing through the center with endpoints on the circumference | A line segment from the center to a point on the circumference |
| Length | Twice the length of the radius | Half the length of the diameter |
| Location | Always passes through the center | Extends from the center to the edge |
| Relationship | Diameter = 2 * Radius | Radius = Diameter / 2 |
| Visual | A line cutting the circle in half | A line from the center to the edge, like a spoke in a wheel |
5. Real-World Applications of the Diameter
The concept of diameter isn’t just confined to textbooks; it has numerous practical applications in various fields.
- Engineering: Determining the size of pipes, shafts, and other circular components.
- Construction: Calculating the amount of material needed for circular structures like tanks and domes.
- Manufacturing: Ensuring the correct dimensions of circular products like wheels, gears, and bearings.
- Everyday Life: Measuring the size of pizzas, coins, and other circular objects.
6. Examples: Putting Knowledge into Practice
Let’s solidify your understanding with some examples:
Example 1: The radius of a circular garden is 8 meters. What is the diameter?
- Diameter = 2 Radius = 2 8 meters = 16 meters
Example 2: A circular table has an area of 30 square feet. Find the diameter.
- Radius = √(Area / π) = √(30 / 3.14159) ≈ 3.09 feet
- Diameter = 2 Radius ≈ 2 3.09 feet ≈ 6.18 feet
Example 3: A bicycle wheel has a diameter of 26 inches. How far does the bicycle travel in one complete rotation of the wheel?
- The distance traveled in one rotation is equal to the circumference.
- Circumference = π Diameter = 3.14159 26 inches ≈ 81.68 inches
7. Common Mistakes to Avoid
When working with diameters and circles, it’s easy to make a few common errors. Here’s what to watch out for:
- Confusing radius and diameter: Remember that the diameter is twice the radius.
- Using the wrong formula: Make sure you’re using the correct formula based on the information you have.
- Forgetting units: Always include the units (e.g., cm, meters, inches) in your answer.
- Rounding errors: Avoid rounding intermediate calculations too early, as this can affect the accuracy of your final answer.
8. Advanced Concepts Related to Diameter
Once you have a firm grasp of the basics, you can explore more advanced concepts related to the diameter:
- Inscribed Circles: A circle that fits perfectly inside a polygon, with its diameter related to the polygon’s dimensions.
- Circumscribed Circles: A circle that passes through all the vertices of a polygon, with its diameter related to the polygon’s dimensions.
- The Golden Ratio: The diameter can be used to construct the golden ratio, a mathematical constant found throughout nature and art.
9. Visualizing the Diameter
Sometimes, the best way to understand a concept is to see it in action. Here are some ways to visualize the diameter:
- Draw a Circle: Use a compass to draw a circle. Then, use a ruler to draw a line through the center of the circle, touching both edges. That line is the diameter.
- Use a Circular Object: Find a circular object, like a plate or a coin. Place a ruler across the center of the object to measure its diameter.
- Online Tools: Use online geometry tools to create circles and explore their properties, including the diameter.
10. Why Is Understanding the Diameter Important?
The diameter is a fundamental concept in geometry with far-reaching implications.
- Problem-Solving: It allows you to solve a wide range of problems related to circles, from finding the circumference and area to calculating volumes and surface areas of spheres and cylinders.
- Design and Engineering: It’s essential for designing and building structures, machines, and other objects that involve circular shapes.
- Critical Thinking: Understanding the diameter helps develop critical thinking skills and spatial reasoning.
11. The Diameter in Different Fields
The diameter is a concept that transcends mathematics and finds applications in various fields:
- Astronomy: Measuring the diameters of planets, stars, and other celestial objects.
- Medicine: Determining the diameter of blood vessels, tumors, and other anatomical structures.
- Sports: Calculating the diameter of balls used in various sports, such as basketballs and soccer balls.
12. Tips and Tricks for Mastering the Diameter
Here are some tips and tricks to help you master the concept of the diameter:
- Practice Regularly: The more you practice solving problems involving the diameter, the better you’ll become.
- Use Visual Aids: Draw diagrams and use physical objects to help you visualize the diameter and its relationship to other properties of the circle.
- Break Down Problems: If you’re facing a complex problem, break it down into smaller, more manageable steps.
- Seek Help When Needed: Don’t hesitate to ask for help from teachers, classmates, or online resources if you’re struggling with the concept.
13. The Diameter and the Number Pi (π)
The diameter plays a crucial role in the definition of the number pi (π). Pi is defined as the ratio of a circle’s circumference to its diameter. This relationship is expressed by the formula:
π = Circumference / Diameter
This means that the circumference of any circle can be found by multiplying its diameter by pi. Pi is an irrational number, meaning that it cannot be expressed as a simple fraction. Its decimal representation goes on forever without repeating.
14. Historical Significance of the Diameter
The concept of the diameter has been around for thousands of years. Ancient civilizations, such as the Egyptians and Babylonians, used the diameter to calculate the circumference and area of circles. The Greek mathematician Archimedes made significant contributions to the understanding of the diameter and its relationship to pi.
15. Common FAQs About Diameters
Let’s tackle some frequently asked questions about diameters.
15.1. Is the Diameter Always the Longest Chord?
Yes, the diameter is always the longest chord in a circle. Any other chord will be shorter than the diameter.
15.2. Can a Diameter Be Curved?
No, by definition, a diameter is a straight line segment.
15.3. Does Every Circle Have a Diameter?
Yes, every circle has an infinite number of diameters. All of them pass through the center and have the same length.
15.4. What Happens if You Don’t Go Through the Center?
If a line segment connects two points on the circumference but doesn’t pass through the center, it’s called a chord, not a diameter.
16. Examples in Art and Architecture
The circle, and therefore the diameter, is a fundamental element in art and architecture.
- Rose Windows: In Gothic cathedrals, large circular windows, known as rose windows, often feature intricate designs based on circles and diameters.
- Domes: The diameters of domes are crucial for calculating their stability and structural integrity.
- Circular Motifs: Many artists use circular motifs in their work, relying on the properties of the diameter to create balanced and harmonious compositions.
17. Fun Facts About Diameters
Here are some fun facts about diameters:
- The word “diameter” comes from the Greek words “dia” (through) and “metros” (measure).
- The diameter of the Earth at the equator is approximately 12,756 kilometers (7,926 miles).
- The diameter of the Sun is about 109 times the diameter of the Earth.
18. Advanced Problems Involving Diameters
Ready for a challenge? Try these advanced problems:
- Problem 1: A square is inscribed in a circle. If the side of the square is 10 cm, what is the diameter of the circle?
- Problem 2: Two circles have diameters of 8 cm and 12 cm, respectively. What is the diameter of a circle whose area is equal to the sum of the areas of the two circles?
- Problem 3: A semicircle is inscribed in a rectangle. If the length of the rectangle is 20 cm and the width is 10 cm, what is the diameter of the semicircle?
19. How to Improve Your Understanding of Diameters
Here are some actionable steps you can take to improve your understanding of diameters:
- Review the Definitions: Make sure you have a clear understanding of the definitions of diameter, radius, circumference, and area.
- Practice Problems: Work through a variety of practice problems, starting with simple ones and gradually moving on to more complex ones.
- Use Online Resources: Take advantage of online resources, such as tutorials, videos, and interactive tools.
- Seek Feedback: Ask your teachers, classmates, or online communities for feedback on your work.
- Apply Your Knowledge: Look for opportunities to apply your knowledge of diameters in real-world situations.
20. The Future of Diameter Studies
The study of circles and their properties, including the diameter, continues to evolve. Researchers are exploring new applications of circles in fields such as:
- Computer Graphics: Creating realistic and efficient representations of circular objects in computer graphics.
- Robotics: Designing robots with circular components for improved mobility and maneuverability.
- Data Analysis: Using circles and their properties to visualize and analyze data.
21. Exploring Polygons Inside Circles
The diameter is often used when exploring polygons inscribed within circles.
- Squares: When a square is inscribed in a circle, the diameter of the circle is the diagonal of the square.
- Equilateral Triangles: When an equilateral triangle is inscribed in a circle, the diameter can be used to find the side length of the triangle.
- Hexagons: A regular hexagon inscribed in a circle has a side length equal to the radius of the circle, making the diameter twice the side length.
22. The Importance of Precision When Measuring Diameters
In many applications, precise measurement of the diameter is critical. This is especially true in engineering, manufacturing, and scientific research.
- Calipers: Calipers are precision instruments used to measure the diameter of objects with high accuracy.
- Micrometers: Micrometers are even more precise than calipers and are used to measure very small diameters.
- Laser Measurement: Laser measurement techniques can be used to measure the diameters of objects remotely and with great precision.
23. Connecting the Diameter to Other Geometric Shapes
The diameter is not just limited to circles. It can also be related to other geometric shapes.
- Spheres: The diameter of a sphere is the distance across the sphere passing through its center.
- Cylinders: The diameter of a cylinder is the diameter of its circular base.
- Cones: The diameter of a cone is the diameter of its circular base.
24. Examples of the Diameter in Nature
Nature is full of examples of circles and diameters.
- Tree Rings: The rings of a tree are approximately circular, and their diameters can be used to estimate the age of the tree.
- Flowers: Many flowers have circular shapes, and their diameters can be used to classify them.
- Fruits and Vegetables: Many fruits and vegetables, such as oranges and tomatoes, are approximately spherical, and their diameters can be used to estimate their volume.
25. Using the Diameter to Calculate Area and Circumference
The diameter is a crucial component in calculating the area and circumference of a circle.
- Area: The area of a circle can be calculated using the formula: Area = π * (Diameter/2)^2
- Circumference: The circumference of a circle can be calculated using the formula: Circumference = π * Diameter
26. The Role of Diameter in Coordinate Geometry
In coordinate geometry, the diameter can be used to find the equation of a circle. If the endpoints of a diameter are known, the center of the circle is simply the midpoint of the diameter. The length of the diameter can then be used to find the radius, and the equation of the circle can be written in the form:
(x – h)^2 + (y – k)^2 = r^2
where (h, k) is the center of the circle and r is the radius.
27. Practical Exercises to Reinforce Understanding
To solidify your understanding of the diameter, try these practical exercises:
- Measure the Diameter: Find several circular objects around your home or classroom and measure their diameters using a ruler or tape measure.
- Calculate the Circumference: Use the diameters you measured in the previous exercise to calculate the circumferences of the circular objects.
- Calculate the Area: Use the diameters you measured in the previous exercises to calculate the areas of the circular objects.
- Solve Word Problems: Find or create word problems that involve the diameter of a circle and practice solving them.
- Draw Circles: Use a compass to draw circles with different diameters and label the diameters, radii, centers, and circumferences.
28. The Relationship Between Diameter and Volume
The diameter is related to the volume of spheres, cylinders, and cones.
- Sphere: The volume of a sphere is given by the formula: Volume = (4/3) π (Diameter/2)^3
- Cylinder: The volume of a cylinder is given by the formula: Volume = π (Diameter/2)^2 Height
- Cone: The volume of a cone is given by the formula: Volume = (1/3) π (Diameter/2)^2 * Height
29. How to Explain the Diameter to a Child
Explaining the diameter to a child can be made easy by using real-world examples.
- Pizza: Cut a pizza in half. The line where you cut is the diameter. It goes straight through the middle.
- Cookie: Take a round cookie. Show how you can draw a line from one side to the other, going through the very center. That’s the diameter.
- Wheel: Look at a bicycle wheel. The distance from one side of the tire to the other, going through the center, is the diameter.
30. The Diameter as a Foundation for Geometry
The diameter is a foundational concept in geometry. Understanding it unlocks a deeper understanding of circles and their properties. From calculating area and circumference to exploring complex geometric shapes, the diameter is an essential tool for anyone interested in mathematics and its applications.
31. The Diameter and Its Role in Circle Theorems
The diameter plays a crucial role in several circle theorems, providing a basis for understanding various geometric relationships.
- Angle in a Semicircle Theorem: This theorem states that the angle inscribed in a semicircle (an angle formed by two lines originating from a point on the circle’s circumference and passing through the endpoints of the diameter) is always a right angle (90 degrees). This theorem is fundamental in solving problems related to angles within circles.
- Perpendicular Bisector Theorem: This theorem states that the perpendicular bisector of a chord (a line segment connecting two points on the circle’s circumference) always passes through the center of the circle. Consequently, if you draw a line from the center of the circle perpendicular to a chord, that line will bisect the chord (divide it into two equal parts). This theorem is useful for finding the center of a circle or determining relationships between chords and the center.
32. Understanding Diameters in 3D Shapes
The concept of diameter extends beyond two-dimensional circles and is equally important in understanding three-dimensional shapes like spheres, cylinders, and cones.
- Spheres: The diameter of a sphere is simply the distance across the sphere, passing through its center. All points on the surface of the sphere are equidistant from the center.
- Cylinders: A cylinder consists of two circular bases connected by a curved surface. The diameter of the cylinder refers to the diameter of these circular bases.
- Cones: A cone has a circular base and tapers to a single point called the apex. The diameter of the cone refers to the diameter of its circular base.
33. The Diameter and Its Uses in Navigation
Although less direct than in geometry, the diameter concept finds indirect applications in navigation, particularly in the use of circular or spherical coordinates and measurements.
- Spherical Coordinates: When navigating on the surface of the Earth, which is approximated as a sphere, calculations often involve angles and distances related to the Earth’s diameter.
- Radar and Sonar: In radar and sonar systems, the range and direction of objects are often determined using circular or spherical patterns, implicitly relying on the understanding of diameters and radii.
34. Common Misconceptions About the Diameter
Let’s address some common misconceptions about the diameter to ensure a clear understanding.
- Misconception: The diameter is just any line across the circle.
- Clarification: The diameter must pass through the center of the circle. A line connecting two points on the circumference but not passing through the center is a chord, not a diameter.
- Misconception: The diameter is the same as the circumference.
- Clarification: The diameter is a straight line across the circle, while the circumference is the distance around the circle. They are related by the formula: Circumference = π * Diameter.
- Misconception: Only perfect circles have diameters.
- Clarification: While the term “diameter” is most commonly associated with perfect circles, the concept can be extended to other shapes that have a circular component or cross-section.
35. How to Use Online Tools to Explore Diameters
Numerous online tools and resources can help you visualize and explore the concept of the diameter.
- Geometry Software: Use interactive geometry software to draw circles, measure their diameters, and explore related properties.
- Online Calculators: Utilize online calculators to quickly find the diameter of a circle given its radius, circumference, or area.
- Educational Websites: Explore educational websites that offer tutorials, videos, and practice problems on the diameter and other circle-related concepts.
36. Real-World Examples of Estimating Diameters
Being able to estimate the diameter of circular objects is a valuable skill in everyday life.
- Estimating the Diameter of a Tree Trunk: You can estimate the diameter of a tree trunk by wrapping your arms around it and measuring the length of your arm span. Then, divide the arm span by π (approximately 3.14) to get an estimate of the diameter.
- Estimating the Diameter of a Circular Table: You can estimate the diameter of a circular table by visually comparing it to a known object, such as a yardstick or a meter stick.
37. Diameter in Relation to Other Circle Parts
Understanding how the diameter relates to other parts of a circle is crucial for a comprehensive understanding of circle geometry.
- Chord: A chord is a line segment that connects two points on the circle’s circumference. The diameter is the longest possible chord in a circle.
- Arc: An arc is a portion of the circle’s circumference. The diameter divides the circle into two semicircles, each with an arc length equal to half the circumference.
- Sector: A sector is a region bounded by two radii and an arc. The diameter can be used to divide a circle into sectors of equal or unequal area.
- Tangent: A tangent is a line that touches the circle at only one point. The radius drawn to the point of tangency is perpendicular to the tangent.
38. Where to Go for More Help with Diameter Questions
If you have more questions about diameters and need additional assistance, here are some resources you can turn to:
- Teachers and Tutors: Seek help from your math teachers or tutors. They can provide personalized explanations and guidance.
- Online Forums: Participate in online math forums where you can ask questions and get answers from other students and experts.
- Educational Websites: Explore educational websites that offer comprehensive resources on circles and other geometry topics.
- Textbooks and Study Guides: Consult your math textbooks and study guides for detailed explanations and examples.
If you’re struggling to grasp these concepts, don’t hesitate to ask your questions on WHAT.EDU.VN. Our community is here to help you!
Address: 888 Question City Plaza, Seattle, WA 98101, United States
Whatsapp: +1 (206) 555-7890
Website: WHAT.EDU.VN
39. Diameter in Different Measurement Systems
The diameter can be expressed in various measurement systems, including:
- Metric System: In the metric system, the diameter is typically measured in millimeters (mm), centimeters (cm), or meters (m).
- Imperial System: In the imperial system, the diameter is typically measured in inches (in) or feet (ft).
When working with diameters in different measurement systems, it’s important to be able to convert between them accurately.
40. The Diameter’s Role in Defining Pi (π)
The diameter plays a pivotal role in defining the fundamental mathematical constant pi (π). Pi is defined as the ratio of a circle’s circumference to its diameter. This relationship is expressed by the formula:
π = Circumference / Diameter
This means that for any circle, the circumference can be calculated by multiplying the diameter by pi. Pi is an irrational number, meaning that it cannot be expressed as a simple fraction. Its decimal representation goes on forever without repeating (approximately 3.14159).
41. Using Diameters to Solve Practical Problems
The concept of the diameter is essential for solving a wide range of practical problems in various fields.
- Construction: Calculating the amount of fencing needed to enclose a circular garden.
- Engineering: Determining the size of pipes needed to transport fluids.
- Manufacturing: Ensuring that circular parts fit together properly.
- Everyday Life: Estimating the amount of frosting needed to cover a circular cake.
42. Exploring the Diameter in Different Contexts
Let’s examine how the concept of the diameter appears in different contexts:
- Mathematics Textbooks: Review how diameters are presented and utilized in your math textbooks. Pay attention to the definitions, formulas, and examples provided.
- Online Tutorials: Explore online tutorials that offer interactive explanations and visualizations of the diameter and its applications.
- Real-World Objects: Identify circular objects in your surroundings and consider how the diameter relates to their properties and functions.
- Geometric Constructions: Practice geometric constructions involving diameters, such as inscribing polygons within circles or constructing tangents to circles.
43. Advanced Concepts: Diameters in Ellipses and Other Shapes
While the primary definition of a diameter applies to circles, analogous concepts exist for other shapes, such as ellipses.
- Ellipses: In an ellipse, the major axis is the longest diameter, passing through the two foci and the center. The minor axis is the shortest diameter, perpendicular to the major axis and also passing through the center.
- Other Shapes: While not strictly “diameters,” similar concepts of longest and shortest axes or dimensions can be applied to other geometric shapes.
44. Estimating Area and Circumference Without Precise Measurements
In situations where precise measurements are not possible or necessary, you can use estimation techniques to approximate the area and circumference of a circle based on its diameter.
- Visual Estimation: Visually compare the circle to known objects or units of measurement to estimate its diameter.
- Using π ≈ 3: For quick estimations, use the approximation π ≈ 3. This will give you a rough estimate of the circumference (Circumference ≈ 3 * Diameter).
- Squaring the Diameter: A rough estimate of the area can be obtained by squaring the diameter and multiplying by a factor slightly less than 1 (Area ≈ 0.75 * Diameter^2).
45. Fun Activities: Diameter-Related Games and Puzzles
Engage in fun activities and games to reinforce your understanding of the diameter.
- Circle Drawing Contest: Challenge friends or classmates to draw the most accurate circle by hand, then measure and compare the diameters.
- Diameter Scavenger Hunt: Organize a scavenger hunt where participants need to find circular objects and measure or estimate their diameters.
- Diameter-Based Puzzles: Solve puzzles that involve finding the diameter of circles within complex geometric figures.
- Create a Diameter-Themed Board Game: Design a board game where players need to use their knowledge of diameters to advance and win.
46. The Diameter and Its Importance in Statistics
While not a direct application, the concept of the diameter can be related to statistical analysis involving circular data or distributions.
- Circular Statistics: In fields like meteorology or animal behavior, data may be collected on directions or angles, which can be represented on a circle. The “diameter” of the data distribution can be related to the spread or variability of the data.
- Visualizing Data: Circles and diameters can be used to create visually appealing and informative graphs and charts for presenting statistical data.
47. Common Problems People Face When Learning About Diameters
Many people encounter similar difficulties when learning about diameters. Here are some common problems and tips for overcoming them:
- Difficulty Distinguishing Radius and Diameter: Use visual aids, like diagrams and physical objects, to clearly differentiate between the radius (from center to edge) and the diameter (across the entire circle through the center).
- Trouble Applying Formulas Correctly: Practice using the formulas for circumference, area, and diameter with a variety of examples. Pay attention to the units of measurement.
- Forgetting to Include Units: Always include the appropriate units (e.g., cm, m, in, ft) when stating the diameter or any other measurement.
- Struggling with Word Problems: Break down word problems into smaller steps, identify the known information, and choose the correct formula to apply.
48. Encouragement to Ask Questions
Learning geometry is a journey, and everyone faces challenges along the way. The most important thing is to stay curious and keep asking questions. There’s no such thing as a “silly” question, and every question you ask brings you one step closer to understanding the concepts. If you’re struggling with diameters or any other geometry topic, don’t hesitate to seek help from teachers, tutors, or online resources.
49. Let WHAT.EDU.VN Help You
Understanding the diameter is vital for anyone exploring geometry or related fields. WHAT.EDU.VN is here to help you on your learning journey, providing clear explanations and easy access to expert assistance.
Remember, learning is a process, and we’re here to support you every step of the way. Don’t hesitate to reach out with your questions.
For more assistance, contact us:
Address: 888 Question City Plaza, Seattle, WA 98101, United States
Whatsapp: +1 (206) 555-7890
Website: WHAT.EDU.VN
50. Ready to Ask Your Questions?
Still have questions about diameters? Don’t hesitate to ask them on what.edu.vn! Our community of experts is ready to provide you with clear, helpful answers. Get the support you need to master this fundamental geometric concept and unlock new levels of understanding.
