Imagine you’re sharing a box of 12 cookies equally among your friends. You can divide them into groups of 2, 3, 4, or even 6 friends, and each friend will get a whole number of cookies. In math, the numbers 2, 3, 4, and 6 are called factors of 12. Understanding factors is a fundamental concept in mathematics, paving the way for more complex topics like fractions, prime numbers, and algebra.
In simple terms, a factor is a number that divides another number evenly, without leaving any remainder. Let’s delve deeper into the definition of factors, explore different methods to find them, and understand their properties and applications in mathematics and real life.
Understanding Factors: The Basics
Factor Definition – Division Perspective
In mathematics, when we talk about factors, we are referring to positive whole numbers (integers). A factor of a number is a whole number that divides the given number exactly, leaving no remainder.
To determine if a number, let’s say ‘x’, is a factor of another number ‘n’, you simply divide ‘n’ by ‘x’. If the remainder is 0, then ‘x’ is indeed a factor of ‘n’. If there’s any remainder other than 0, then ‘x’ is not a factor of ‘n’.
Let’s look at some examples to make this clearer:
| Division | Remainder | Is the number a factor? |
|---|---|---|
| $15 div 3 = 5$ | Remainder = 0 | Yes, 3 is a factor of 15. |
| $24 div 6 = 4$ | Remainder = 0 | Yes, 6 is a factor of 24. |
| $17 div 5 = 3$ | Remainder = 2 | No, 5 is not a factor of 17. |
| $9 div 9 = 1$ | Remainder = 0 | Yes, 9 is a factor of 9. |
It’s important to remember that factors are always positive integers. They cannot be fractions or decimals. Also, zero (0) cannot be a factor of any number because division by zero is undefined in mathematics.
Factor Definition – Multiplication Perspective
We know that multiplication and division are inverse operations. Therefore, we can also define factors in terms of multiplication.
If a number can be expressed as a product of two whole numbers, then those two numbers are factors of the original number. A simple way to remember this is: if we have two whole numbers, ‘a’ and ‘b’, and their product is ‘ab’, then both ‘a’ and ‘b’ are factors of ‘ab’.
Consider these examples:
| Product | Factors |
|---|---|
| $4 times 5 = 20$ | Both 4 and 5 are factors of 20. |
| $3 times 8 = 24$ | Both 3 and 8 are factors of 24. |
| $7 times 9 = 63$ | Both 7 and 9 are factors of 63. |
| $1 times 11 = 11$ | Both 1 and 11 are factors of 11. |
Understanding factors from both the division and multiplication perspectives gives you a more comprehensive grasp of this concept. They are two sides of the same coin!
How to Find Factors: Methods
There are primarily two straightforward methods to find the factors of a number: the multiplication method and the division method. Let’s explore each in detail.
Multiplication Method
The multiplication method involves finding pairs of whole numbers that, when multiplied together, result in the number you are interested in.
Here’s how to use the multiplication method step-by-step:
-
Start with 1: Begin by checking if 1 is a factor. It always is, as 1 multiplied by any number equals that number itself. So, for any number ‘n’, $1 times n = n$.
-
Check subsequent whole numbers: Systematically check whole numbers (2, 3, 4, and so on) to see if they can be multiplied by another whole number to give you the original number.
-
Find pairs: For each number you check, if you find a whole number that multiplies with it to produce the original number, you’ve found a factor pair.
-
Continue until pairs repeat or cross: Continue this process until you start getting repeated factor pairs (numbers in reverse order) or when the smaller factor in your pair becomes larger than the square root of the original number.
Let’s illustrate with examples:
Example 1: Find the factors of 12.
- $1 times 12 = 12$. So, 1 and 12 are factors.
- $2 times 6 = 12$. So, 2 and 6 are factors.
- $3 times 4 = 12$. So, 3 and 4 are factors.
- $4 times 3 = 12$. We’ve already encountered 4 and 3. We can stop here as the pairs will start repeating.
Therefore, the factors of 12 are 1, 2, 3, 4, 6, and 12.
Example 2: Find the factors of 36.
- $1 times 36 = 36$. Factors: 1, 36.
- $2 times 18 = 36$. Factors: 2, 18.
- $3 times 12 = 36$. Factors: 3, 12.
- $4 times 9 = 36$. Factors: 4, 9.
- $6 times 6 = 36$. Factors: 6 (only list once).
- $9 times 4 = 36$. Pair repetition, we stop.
Thus, the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.
Division Method
The division method involves systematically dividing the number you’re interested in by whole numbers, starting from 1, and checking for remainders.
Here’s the division method in steps:
-
Start dividing by 1: Divide the number by 1. It will always divide evenly, confirming 1 as a factor.
-
Divide by subsequent whole numbers: Divide the number by 2, 3, 4, and so on, up to the number itself.
-
Check for zero remainder: For each division, check if the remainder is 0. If the remainder is 0, then the number you divided by is a factor.
-
Quotient is also a factor: When you find a factor using division, the quotient you get from the division is also a factor.
Let’s see this method in action:
Example: Find all factors of 18.
| Division | Is the number a factor of 18? | Factors Found |
|---|---|---|
| $18 div 1 = 18$, Remainder = 0 | Yes | 1, 18 |
| $18 div 2 = 9$, Remainder = 0 | Yes | 2, 9 |
| $18 div 3 = 6$, Remainder = 0 | Yes | 3, 6 |
| $18 div 4 = 4$, Remainder = 2 | No | |
| $18 div 5 = 3$, Remainder = 3 | No | |
| $18 div 6 = 3$, Remainder = 0 | Yes | 6 (already listed), 3 (already listed) |
| … and so on until 18 |
Continuing this process, you’ll find that the factors of 18 are 1, 2, 3, 6, 9, and 18.
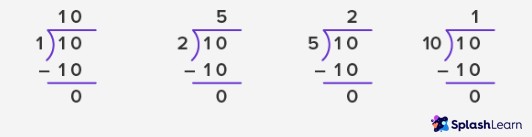Finding factors of 10 by division method
Properties of Factors
Factors have several interesting properties that are always true for any number (except for 0 and 1 in some cases). Understanding these properties can further solidify your understanding of factors.
-
1 is the smallest factor: For any whole number, 1 is always a factor. This is because every number is divisible by 1.
-
The number itself is the largest factor: Every number is a factor of itself. When you divide a number by itself, the result is always 1 with no remainder.
-
Finite number of factors: Every whole number has a limited, countable number of factors. Unlike multiples, which are infinite, factors are always finite.
-
Factors are less than or equal to the number: A factor of a number will always be less than or equal to the number itself. It can never be larger than the number.
-
Minimum of two factors (for integers greater than 1): Every integer greater than 1 has at least two factors: 1 and the number itself. Numbers with exactly two factors are called prime numbers.
Factor Pairs
A factor pair is simply a set of two factors that, when multiplied together, give you the original number. We encountered factor pairs in the multiplication method earlier.
For instance, for the number 12, the factor pairs are (1, 12), (2, 6), and (3, 4).
While we usually consider positive factors, factor pairs can also include negative integers. For every positive factor pair, there’s a corresponding negative factor pair because the product of two negative numbers is a positive number.
Let’s see factor pairs for 24:
| Positive Factor Pairs of 24 | Negative Factor Pairs of 24 |
|---|---|
| $1 times 24 = 24 Rightarrow (1, 24)$ | $(-1) times (-24) = 24 Rightarrow (-1, -24)$ |
| $2 times 12 = 24 Rightarrow (2, 12)$ | $(-2) times (-12) = 24 Rightarrow (-2, -12)$ |
| $3 times 8 = 24 Rightarrow (3, 8)$ | $(-3) times (-8) = 24 Rightarrow (-3, -8)$ |
| $4 times 6 = 24 Rightarrow (4, 6)$ | $(-4) times (-6) = 24 Rightarrow (-4, -6)$ |
Types of Factors
While “factor” itself is the primary term, there are some related terms that are important in mathematics:
Prime Factors
A prime factor of a number is a factor that is also a prime number. A prime number is a whole number greater than 1 that has only two factors: 1 and itself (e.g., 2, 3, 5, 7, 11…).
To find the prime factors of a number, you first find all its factors and then identify which of those factors are prime numbers.
For example, let’s find the prime factors of 30:
Factors of 30 are: 1, 2, 3, 5, 6, 10, 15, 30.
From this list, the prime factors are 2, 3, and 5.
Greatest Common Factor (GCF)
The Greatest Common Factor (GCF) of two or more numbers is the largest factor that is common to all of them. Finding the GCF is useful in simplifying fractions and in various algebraic problems.
To find the GCF of two numbers, you can:
- List all factors of each number.
- Identify the common factors from both lists.
- The largest among these common factors is the GCF.
Example: Find the GCF of 12 and 18.
Factors of 12: 1, 2, 3, 4, 6, 12.
Factors of 18: 1, 2, 3, 6, 9, 18.
Common factors: 1, 2, 3, 6.
The greatest common factor (GCF) is 6.
Prime Factorization
Prime factorization is the process of expressing a number as a product of its prime factors. Every composite number (a number with more than two factors) can be uniquely expressed as a product of prime numbers.
To find the prime factorization of a number, you can use a method called factor tree or repeated division.
Example 1: Prime factorization of 36.
Using repeated division:
- Start by dividing 36 by the smallest prime number, 2: $36 div 2 = 18$.
- Divide the quotient (18) by 2 again: $18 div 2 = 9$.
- 9 is not divisible by 2, so try the next prime number, 3: $9 div 3 = 3$.
- 3 is a prime number, so we stop.
The prime factors used in the division are 2, 2, and 3. Therefore, the prime factorization of 36 is $2 times 2 times 3 times 3$, which can be written as $2^2 times 3^2$.
Example 2: Prime factorization of 60.
$60 = 2 times 30$
$30 = 2 times 15$
$15 = 3 times 5$
So, $60 = 2 times 2 times 3 times 5 = 2^2 times 3 times 5$.
Real-Life Applications of Factors
Factors are not just abstract mathematical concepts; they have practical applications in everyday life.
-
Equal Division and Sharing: As we started with, factors help in dividing things equally. Whether it’s sharing food, dividing tasks, or distributing resources, factors ensure fair and even distribution. For example, if you have 30 students and want to divide them into equal groups, the factors of 30 (2, 3, 5, 6, 10, 15) tell you the possible group sizes.
-
Money and Finance: Currency systems are based on factors. For instance, a dollar is divided into 100 cents, and denominations like quarters (25 cents), dimes (10 cents), and nickels (5 cents) are factors of 100, making transactions and exchanges easier.
-
Time and Measurement: Units of time (hours, minutes, seconds) and length (feet, inches, yards) are related through factors. For example, there are 60 minutes in an hour, and 12 inches in a foot. These factor relationships are crucial for timekeeping, measurements, and conversions.
-
Arrangement and Organization: Factors are useful when arranging items in rows and columns or organizing data. For example, if you have 24 items to display in a rectangular array, the factor pairs of 24 (1×24, 2×12, 3×8, 4×6) give you the possible arrangements.
Interesting Facts about Factors
-
Composite Numbers: A number with more than two factors is called a composite number. All composite numbers can be broken down into prime factors.
-
Factors are always integers: Factors are always whole numbers; they are never decimals or fractions.
-
2 as a factor of even numbers: Every even number is divisible by 2, meaning 2 is a factor of all even numbers.
-
5 as a factor for numbers ending in 0 or 5: Any number ending in 0 or 5 is divisible by 5, so 5 is a factor of such numbers.
-
10 as a factor for numbers ending in 0: Numbers ending in 0 are divisible by 10, making 10 a factor. In fact, both 2 and 5 are also factors of numbers ending in 0.
-
Number of Factors from Prime Factorization: If the prime factorization of a number is given as $p^{a} times q^{b} times r^{c}…$, where p, q, r… are prime factors and a, b, c… are their exponents, then the total number of factors of that number is given by $(a+1) times (b+1) times (c+1) times …$. For example, for $12 = 2^2 times 3^1$, the number of factors is $(2+1) times (1+1) = 3 times 2 = 6$. The factors of 12 are indeed 1, 2, 3, 4, 6, and 12.
Solved Examples on Factor in Math
Example 1: Find all the factors of 45.
Solution:
Using the division method:
$45 div 1 = 45$ (Factor: 1, 45)
$45 div 3 = 15$ (Factor: 3, 15)
$45 div 5 = 9$ (Factor: 5, 9)
$45 div 6, 7, 8$ (Not divisible)
$45 div 9 = 5$ (Factor: 9, 5 – repeated pair)
The factors of 45 are 1, 3, 5, 9, 15, and 45.
Example 2: Determine if 7 is a factor of 53.
Solution:
Divide 53 by 7: $53 div 7 = 7$ with a remainder of 4.
Since the remainder is not 0, 7 is not a factor of 53.
Example 3: Find the prime factorization of 72.
Solution:
Using repeated division:
$72 div 2 = 36$
$36 div 2 = 18$
$18 div 2 = 9$
$9 div 3 = 3$
$3 div 3 = 1$
Prime factors are 2, 2, 2, 3, 3. Prime factorization of 72 is $2^3 times 3^2$.
Example 4: Sarah wants to arrange 32 flower pots in rectangular arrays for a garden show. What are the possible number of rows and columns she can use?
Solution:
We need to find the factor pairs of 32.
$1 times 32 = 32$
$2 times 16 = 32$
$4 times 8 = 32$
The factor pairs are (1, 32), (2, 16), (4, 8). Sarah can arrange the pots in:
- 1 row and 32 columns
- 32 rows and 1 column
- 2 rows and 16 columns
- 16 rows and 2 columns
- 4 rows and 8 columns
- 8 rows and 4 columns
Conclusion
Understanding factors is a crucial step in building a strong foundation in mathematics. Factors are not just numbers that divide evenly; they are fundamental building blocks in number theory and have wide-ranging applications in real-world scenarios. From simplifying fractions to organizing items and understanding financial systems, the concept of factors is woven into the fabric of mathematics and our daily lives. By mastering factors, you unlock a deeper understanding of how numbers work and prepare yourself for more advanced mathematical concepts.
