In the realm of mathematics, the concept of a function is fundamental. It acts as a rule, an expression, or a law that precisely describes the relationship between two variables: an independent variable and a dependent variable. Functions are not just confined to textbooks; they are ubiquitous, forming the backbone for expressing relationships in various scientific disciplines.
But What Is A Function In Math in more precise terms? Let’s delve deeper into the definition, types, and significance of functions.
Defining a Function: The Dirichlet Definition
The modern, rigorous definition of a function was formalized in 1837 by the German mathematician Peter Dirichlet. His definition provides a clear and unambiguous understanding of what constitutes a function:
If a variable y is so related to a variable x that whenever a numerical value is assigned to x, there is a rule according to which a unique value of y is determined, then y is said to be a function of the independent variable x.
This means for every input value of x, there is only one corresponding output value of y. We commonly express this relationship using the notation y = f(x), read as “f of x.” The key aspect here is uniqueness: for a given x, f(x) can only have one value.
In the language of set theory, a function maps each element x from one set (the domain) to a unique element f(x) in another set (the range). The domain encompasses all possible input values for x, while the range includes all possible output values of f(x) generated from the domain. Functions can be represented by various symbols such as g(x) or P(x), particularly when the function’s specific nature is not yet defined.
Common Types of Functions in Mathematics
Many familiar mathematical formulas represent specific types of functions. Let’s explore some common categories:
Polynomial Functions
Polynomial functions are among the most versatile and widely studied functions in mathematics. They have the general form:
P(x) = a0 + a1x + a2x2 + ⋯ + anxn
Here, the coefficients (a0, a1, a2,…, an) are constants, x is the variable, and the exponents are non-negative integers. The highest power of x dictates the degree of the polynomial, which in turn characterizes the function.
- Linear functions (degree 1): f(x) = a0 + a1x (e.g., y = 2x + 1)
- Quadratic functions (degree 2): f(x) = a0 + a1x + a2x2 (e.g., y = x2 – 3x + 2)
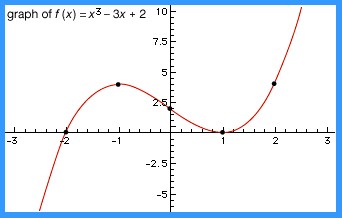
- Cubic functions (degree 3): f(x) = a0 + a1x + a2x2 + a3x3 (e.g., y = x3 − 3x + 2)
- Quartic functions (degree 4), and quintic functions (degree 5) follow the same pattern with increasing degrees.
Polynomial functions are incredibly useful because they can approximate virtually any relationship involving real numbers with sufficient accuracy.
The graph of a cubic equation f(x) = x3 − 3x + 2, showcasing points where curvature changes occur.
Trigonometric Functions
Trigonometric functions, such as sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x), and cosecant (csc x), are another fundamental class of functions studied since antiquity. These functions relate angles of a right triangle to ratios of its sides. The input x typically represents an angle, and the output is a ratio.
A key characteristic of trigonometric functions is their periodic nature. This means their values repeat at regular intervals. For instance, sine and cosine functions repeat every 2π, while tangent and cotangent functions repeat every π. This periodicity makes them invaluable for modeling phenomena that exhibit cyclical behavior, such as oscillations, waves, and rotations.
Graphs illustrating the periodic nature of trigonometric functions: sine, cosine, tangent, and cotangent. Sine and cosine repeat every 2π, while tangent and cotangent repeat every π.
Exponential and Logarithmic Functions
Exponential functions take the form y = ax, where a is a positive constant base and x is the exponent, ranging over all real numbers. The most prominent exponential function is y = ex (or exp(x)), where e is the base of natural logarithms, approximately 2.7182818….
Logarithmic functions are the inverse of exponential functions. If y = ex, then x = ln(y), where ln denotes the natural logarithm. In general, if y = ax, then x = loga(y).
Functions that are not algebraic, like exponential and trigonometric functions, are known as transcendental functions.
Complex Functions
While less immediately tangible, complex functions, which involve complex numbers as variables, are crucial in many advanced applications. Complex numbers extend the real number system by including the imaginary unit i, where i2 = -1. A complex variable z is expressed as z = x + iy, where x and y are real numbers.
A complex function f(z) can be decomposed into real and imaginary parts: f(z) = P(x, y) + iQ(x, y), where P(x, y) and Q(x, y) are real-valued functions of two real variables x and y.
Complex functions find applications in diverse fields like electrical engineering, aerodynamics, and quantum mechanics.
A point visualized in the complex plane, demonstrating the real and imaginary axes. Unlike real numbers on a number line, complex numbers require a plane with two axes: one for the real component and one for the imaginary component.
Conclusion: The Power of Functions in Mathematics
In summary, what is a function in math? It is a rule that assigns each input value to a unique output value. Functions are the language of relationships in mathematics and science. From simple polynomial expressions to complex trigonometric and exponential forms, and even extending to the realm of complex numbers, functions provide a powerful framework for describing, modeling, and understanding the world around us. Their versatility and fundamental nature make them an indispensable tool in mathematical analysis and its applications.