What is a half-life? It’s a fundamental concept in nuclear physics and chemistry, describing how long it takes for half of a radioactive substance to decay. At WHAT.EDU.VN, we aim to simplify complex scientific ideas. We’ll explore half-life definition, half-life calculation, and half-life applications, offering clear answers and fostering curiosity. Discover how nuclear decay and isotope half-life work!
1. Defining Half-Life: The Essence of Radioactive Decay
The half-life (t₁/₂) of a radioactive isotope is the time required for one-half of the atoms in a sample to decay. This decay occurs through the emission of particles or energy, transforming the original isotope into a different element or isotope. Half-life is a fundamental property of each radioactive isotope and is independent of external factors like temperature, pressure, or chemical environment. Think of it as the isotope’s internal clock, ticking away at a constant rate regardless of what’s happening around it. The concept of half-life is crucial in various fields, from medicine to archaeology, for dating materials and understanding radioactive processes.
Understanding decay rates and nuclear stability is key. The shorter the half-life, the faster the decay process. Some isotopes have half-lives of mere fractions of a second, while others persist for billions of years. This variability makes radioactive isotopes useful for dating objects across vastly different timescales.
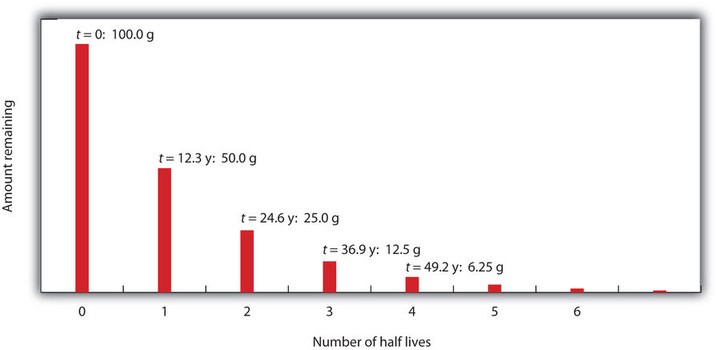
Radioactive decay curve showing the reduction of radioactive material over successive half-lives.
2. The Mathematics of Half-Life: Formulas and Calculations
2.1. The Fundamental Half-Life Equation
The amount of a radioactive substance remaining after a certain time can be calculated using the following equation:
N(t) = N₀ * (1/2)^(t/t₁/₂)Where:
- N(t) is the amount of the substance remaining after time t.
- N₀ is the initial amount of the substance.
- t is the time elapsed.
- t₁/₂ is the half-life of the substance.
This equation demonstrates exponential decay. Each half-life reduces the amount of the substance by half. The ratio t/t₁/₂ represents the number of half-lives that have passed. This equation is the cornerstone of half-life calculations and allows us to predict the amount of radioactive material present at any given time.
2.2. Calculating Remaining Amount After ‘n’ Half-Lives
A simplified version of the equation can be used if you know the number of half-lives that have passed:
Remaining Amount = Initial Amount * (1/2)^nWhere ‘n’ is the number of half-lives. This is particularly useful for quick estimations and understanding the rate of decay. For example, after 3 half-lives, only 1/8 (1/2 1/2 1/2) of the original substance remains.
2.3. Determining Half-Life From Decay Data
Sometimes, you might need to determine the half-life of a substance based on experimental data. This involves rearranging the half-life equation and using logarithms. The process typically involves measuring the initial amount of a substance (N₀), measuring the amount remaining (N(t)) after a certain time (t), and then solving for t₁/₂.
The rearranged formula is:
t₁/₂ = t / (log₂(N₀/N(t)))Where log₂ is the base-2 logarithm. Most calculators don’t have a direct log₂ function, so you can use the change of base formula: log₂(x) = log(x) / log(2), where log is the base-10 logarithm or the natural logarithm (ln). Understanding how to calculate half-life from decay data is vital in fields like nuclear chemistry and environmental science.
2.4. Examples of Half-Life Calculations
Example 1: Fluorine-20 Decay
Fluorine-20 (²⁰F) has a half-life of 11.0 seconds. If you start with a 5.00 g sample, how much ²⁰F will remain after 44.0 seconds?
Solution:
- Determine the number of half-lives: 44.0 seconds / 11.0 seconds/half-life = 4 half-lives
- Use the simplified equation: Remaining Amount = 5.00 g (1/2)⁴ = 5.00 g (1/16) = 0.3125 g
Therefore, 0.3125 g of ²⁰F will remain after 44.0 seconds.
Example 2: Determining Half-Life of Actinium-225
A sample of Actinium-225 (²²⁵Ac) originally contained 80 grams. After 50 days, only 2.5 grams of ²²⁵Ac remain. What is the half-life of ²²⁵Ac?
Solution:
- Use the rearranged formula: t₁/₂ = t / (log₂(N₀/N(t)))
- Substitute the values: t₁/₂ = 50 days / (log₂(80 g / 2.5 g)) = 50 days / (log₂(32))
- Since 2⁵ = 32, log₂(32) = 5.
- Calculate the half-life: t₁/₂ = 50 days / 5 = 10 days
Therefore, the half-life of ²²⁵Ac is 10 days.
Example 3: Iodine-125 Activity
Iodine-125 (¹²⁵I) has a half-life of 59.4 days. If the initial activity of a sample is 32,000 counts per minute (cpm), what will the activity be after 178.2 days?
Solution:
- Determine the number of half-lives: 178.2 days / 59.4 days/half-life = 3 half-lives
- Use the equation: N(t) = N₀ * (1/2)^(t/t₁/₂)
- Substitute the values: N(178.2) = 32,000 cpm (1/2)³ = 32,000 cpm (1/8) = 4,000 cpm
Therefore, the activity of the ¹²⁵I sample will be 4,000 cpm after 178.2 days.
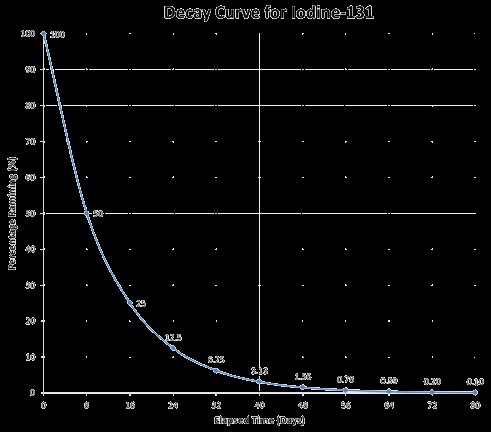
A typical radioactive decay curve showing the exponential decrease in activity over time.
3. Applications of Half-Life: From Dating to Medicine
The concept of half-life has wide-ranging applications across various scientific disciplines:
3.1. Radiometric Dating: Unraveling the Past
Radiometric dating techniques use the known half-lives of radioactive isotopes to determine the age of rocks, fossils, and archaeological artifacts. Carbon-14 dating is used for organic materials up to about 50,000 years old, while isotopes with longer half-lives, such as uranium-238 and potassium-40, are used to date geological formations millions or even billions of years old. This allows scientists to reconstruct the history of the Earth and the evolution of life.
3.2. Medical Applications: Diagnosis and Treatment
Radioactive isotopes are used in medical imaging techniques such as PET scans and SPECT scans to diagnose diseases. They are also used in radiation therapy to treat cancer. The half-life of the isotope is carefully chosen to provide the necessary radiation dose while minimizing exposure to healthy tissues. For example, iodine-131, with a half-life of 8 days, is used to treat thyroid cancer.
3.3. Nuclear Medicine and Tracers
Radioactive tracers are used to follow the movement of substances within the body or in industrial processes. By incorporating a radioactive isotope into a molecule, scientists can track its path and distribution using radiation detectors. This technique is valuable in understanding metabolic pathways and optimizing industrial processes.
3.4. Nuclear Waste Management: Long-Term Storage
Understanding half-lives is crucial in managing nuclear waste. Radioactive waste contains isotopes with varying half-lives, some of which can remain hazardous for thousands of years. This necessitates long-term storage solutions that can safely contain the waste until the radioactivity has decayed to safe levels. The design of these storage facilities must consider the half-lives of the isotopes present and the potential for environmental contamination.
3.5. Industrial Applications: Gauging and Quality Control
Radioactive isotopes are used in various industrial applications, such as gauging the thickness of materials, detecting leaks in pipelines, and sterilizing medical equipment. The half-life of the isotope used is chosen based on the specific application and the desired level of penetration and detection.
4. Factors Affecting Half-Life: Is It Truly Constant?
While the half-life of a radioactive isotope is generally considered constant, it’s important to understand the nuances:
4.1. External Conditions: Minimal Impact
For most practical purposes, external conditions such as temperature, pressure, and chemical environment have a negligible effect on half-life. The decay process is governed by the internal structure of the nucleus and is largely unaffected by external factors.
4.2. Extreme Conditions: Minor Variations
Under extreme conditions, such as those found in the cores of stars or in particle accelerators, minor variations in half-life have been observed. These variations are typically due to changes in the interaction of the nucleus with its surrounding environment. However, these effects are generally insignificant under normal laboratory or environmental conditions.
4.3. Electron Capture: A Notable Exception
Electron capture is a type of radioactive decay where an atomic nucleus absorbs an inner-shell electron. The half-life of isotopes that decay through electron capture can be slightly affected by the chemical environment, as the electron density around the nucleus can influence the probability of electron capture. However, these effects are usually small and only significant in specific cases.
4.4. Quantum Tunneling: The Underlying Mechanism
Radioactive decay is a quantum mechanical process governed by the laws of probability. The nucleus must overcome a potential energy barrier to emit a particle or undergo a transformation. Quantum tunneling allows the particle to pass through the barrier even if it doesn’t have enough energy to overcome it classically. The half-life is determined by the probability of this tunneling process occurring.
5. Half-Life vs. Biological Half-Life: A Key Distinction
In pharmacology and toxicology, the term “biological half-life” is used to describe the time it takes for the body to eliminate half of a substance, such as a drug or a toxin. This is different from the radioactive half-life, which refers to the decay of a radioactive isotope. The biological half-life depends on factors such as metabolism, excretion, and distribution within the body. Understanding both types of half-life is crucial in determining the appropriate dosage and frequency of medications and in assessing the environmental impact of pollutants.
6. Common Misconceptions About Half-Life
6.1. Complete Decay After Two Half-Lives
A common misconception is that a radioactive substance will completely decay after two half-lives. In reality, after each half-life, half of the remaining substance decays, so there is always some amount of the original substance left, although it may be a very small amount.
6.2. Half-Life Indicates Longevity
Another misconception is that a short half-life means the substance is not dangerous. While a short half-life means the substance decays quickly, it also means that it emits radiation at a higher rate, which can be harmful in the short term. Conversely, a long half-life means the substance decays slowly, but it remains radioactive for a much longer period.
6.3. External Factors Affect Half-Life
As discussed earlier, external factors generally do not significantly affect the half-life of a radioactive isotope. It’s an intrinsic property of the isotope itself.
7. Half-Lives of Common Isotopes: A Quick Reference Guide
Here’s a table listing the half-lives of some common radioactive isotopes:
| Isotope | Half-Life | Application |
|---|---|---|
| Carbon-14 | 5,730 years | Radiocarbon dating |
| Uranium-238 | 4.47 billion years | Dating geological formations |
| Iodine-131 | 8.02 days | Treatment of thyroid cancer |
| Cobalt-60 | 5.27 years | Radiation therapy, industrial gauging |
| Technetium-99m | 6 hours | Medical imaging |
| Potassium-40 | 1.25 billion years | Dating ancient rocks |
| Plutonium-239 | 24,100 years | Nuclear weapons, nuclear reactors |
| Americium-241 | 432.2 years | Smoke detectors |
| Cesium-137 | 30.17 years | Industrial gauges, radiation therapy |
8. The Importance of Accurate Half-Life Measurements
Accurate half-life measurements are essential for various scientific and technological applications. These measurements rely on precise experimental techniques and sophisticated statistical analysis. Any uncertainty in the half-life value can lead to errors in dating, medical treatments, and nuclear waste management. Scientists continuously refine half-life measurements to improve the accuracy and reliability of these applications.
9. Real-World Examples of Half-Life in Action
9.1. Chernobyl and Fukushima: Understanding Long-Term Contamination
The Chernobyl and Fukushima nuclear disasters released large amounts of radioactive isotopes into the environment. Understanding the half-lives of these isotopes, such as cesium-137 and strontium-90, is crucial for assessing the long-term environmental and health impacts of these events. These isotopes have relatively long half-lives, meaning that the contaminated areas will remain radioactive for many years to come.
9.2. The Shroud of Turin: Carbon-14 Dating Controversy
The Shroud of Turin, a linen cloth believed by some to be the burial shroud of Jesus, has been the subject of much debate. Carbon-14 dating tests conducted in 1988 dated the shroud to the Middle Ages, between 1260 and 1390 AD. However, some argue that the carbon-14 dating results are inaccurate due to contamination or other factors. This controversy highlights the importance of careful sample preparation and accurate measurements in radiometric dating.
9.3. Medical Isotopes in Cancer Treatment
Medical isotopes play a vital role in cancer treatment. For example, cobalt-60 is used in radiation therapy to kill cancer cells, while iodine-131 is used to treat thyroid cancer. The half-lives of these isotopes are carefully chosen to provide the necessary radiation dose while minimizing damage to healthy tissues. The development of new medical isotopes with improved properties is an ongoing area of research.
10. Further Exploration of Radioactive Decay
10.1. Types of Radioactive Decay: Alpha, Beta, and Gamma
Radioactive decay can occur through different mechanisms, including alpha decay, beta decay, and gamma decay. Alpha decay involves the emission of an alpha particle (a helium nucleus) from the nucleus. Beta decay involves the emission of a beta particle (an electron or a positron) from the nucleus. Gamma decay involves the emission of a gamma ray (a high-energy photon) from the nucleus. Each type of decay has its own characteristic properties and affects the nucleus differently.
10.2. Decay Series: Tracing the Transformation of Elements
Some radioactive isotopes undergo a series of decays, transforming from one element to another until they reach a stable isotope. This is known as a decay series. For example, uranium-238 undergoes a series of 14 decays before finally becoming stable lead-206. Understanding decay series is important in geology and environmental science for tracing the origin and movement of radioactive materials.
10.3. Nuclear Fission and Fusion: Harnessing the Power of the Atom
Nuclear fission and fusion are nuclear reactions that involve the splitting or combining of atomic nuclei, respectively. These reactions release enormous amounts of energy and are the basis for nuclear power and nuclear weapons. Understanding half-lives and radioactive decay is essential for controlling and managing these powerful technologies.
11. The Future of Half-Life Research
Research on half-lives and radioactive decay continues to advance, with new discoveries and applications emerging regularly. Scientists are exploring new isotopes and decay modes, developing more accurate measurement techniques, and using radioactive isotopes in innovative ways in medicine, industry, and environmental science. The future of half-life research promises to bring even greater understanding and benefits to society.
12. Answering Your Half-Life Questions: A FAQ
Q1: What exactly is a half-life?
A1: Half-life is the time it takes for half of a radioactive substance to decay.
Q2: Is half-life affected by temperature?
A2: Generally, no. Half-life is a constant, unaffected by normal temperature or pressure changes.
Q3: How is half-life used in carbon dating?
A3: Carbon-14’s half-life (5,730 years) helps scientists determine the age of organic materials.
Q4: Can half-life be used to treat cancer?
A4: Yes, isotopes with specific half-lives are used in radiation therapy to target and destroy cancer cells.
Q5: What happens after one half-life?
A5: Half of the original radioactive substance remains; the other half has decayed into a different element.
Q6: How does half-life relate to nuclear waste?
A6: Understanding the half-lives of isotopes in nuclear waste is crucial for safe long-term storage.
Q7: Is there a limit to how many half-lives a substance can go through?
A7: No, a substance can theoretically go through an infinite number of half-lives, but the amount remaining becomes infinitesimally small.
Q8: What is the difference between half-life and biological half-life?
A8: Half-life refers to radioactive decay, while biological half-life refers to how long it takes the body to eliminate half of a substance.
Q9: How do scientists measure half-life?
A9: Scientists use radiation detectors and statistical analysis to measure the rate of decay and determine the half-life.
Q10: What are some common isotopes and their half-lives?
A10: Carbon-14 (5,730 years), Uranium-238 (4.47 billion years), and Iodine-131 (8.02 days) are common examples.
Do you have more questions about half-life or other science topics? Don’t hesitate to ask! At WHAT.EDU.VN, we provide free answers to all your questions. Contact us today at 888 Question City Plaza, Seattle, WA 98101, United States or via WhatsApp at +1 (206) 555-7890. You can also visit our website at WHAT.EDU.VN. We are here to help you understand the world around you.
Ready to explore more? Ask your questions now at what.edu.vn and get the answers you need, completely free!