What Is An Integer? Definition, Properties, and Examples

What is an integer? Discover the definition of an integer, its properties, and real-world examples at WHAT.EDU.VN. We’ll explore integer operations, number lines, and more to solidify your understanding. Get clear explanations and examples to improve your knowledge of whole numbers and their place in mathematics, as well as signed numbers and rational numbers.

1. What is an Integer?

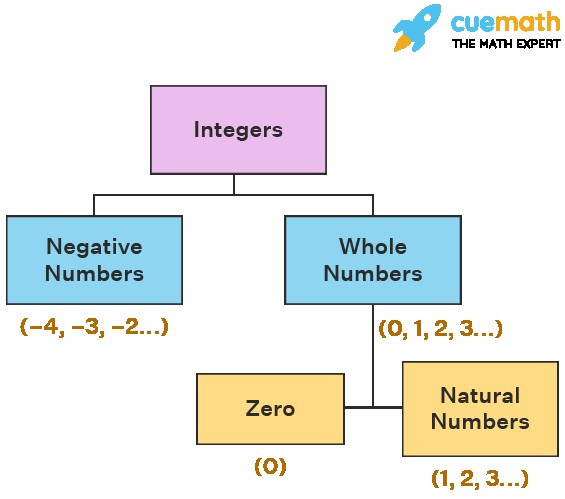
An integer is a fundamental concept in mathematics. It is a whole number (not a fraction) that can be positive, negative, or zero. This means integers include numbers like -3, -2, -1, 0, 1, 2, 3, and so on. They are distinct from numbers with decimal or fractional parts. Understanding what is an integer is crucial because they form the basis for many mathematical operations and concepts.

The term “integer” comes from the Latin word “integer,” meaning “whole” or “intact.” This perfectly describes the nature of integers as complete, unbroken numbers.

1.1. Integer Definition

An integer is defined as a number without any decimal or fractional component. It encompasses positive numbers, negative numbers, and zero. Examples of integers include -10, -1, 0, 5, 25, and 100. In contrast, numbers like 2.5, -3.14, or 1/2 are not integers because they contain decimal or fractional parts.

The set of all integers is typically denoted by the symbol Z (from the German word “Zahlen,” meaning numbers). This set extends infinitely in both the positive and negative directions.

1.2. Components of Integers

The set of integers comprises three main components:

• Positive Integers: These are integers greater than zero, such as 1, 2, 3, 4, and so on. They are the same as natural numbers or counting numbers.
• Negative Integers: These are integers less than zero, such as -1, -2, -3, -4, and so on. They represent values below zero.
• Zero: Zero is an integer that is neither positive nor negative. It is the neutral element in addition and subtraction.

1.3. Set of Integers (Z)

The set of integers, denoted as Z, can be represented as follows:

Z = {…, -3, -2, -1, 0, 1, 2, 3, …}

This set includes all whole numbers, both positive and negative, along with zero. It is an infinite set, meaning it continues indefinitely in both directions.

Integers are essential because they provide a foundation for more complex mathematical concepts and are used in various real-world applications. Whether you’re calculating finances, measuring temperatures, or dealing with computer programming, integers are indispensable.

2. Integers on a Number Line

A number line is a visual representation of numbers on a straight line. It’s a valuable tool for understanding the order and relationships between numbers, including integers. The number line extends infinitely in both directions, with zero typically placed at the center.

2.1. Representing Integers on a Number Line

Integers are represented as points on the number line. Positive integers are located to the right of zero, while negative integers are located to the left of zero. The distance between each consecutive integer is equal, providing a clear visual representation of their relative values.

When graphing integers on a number line, follow these guidelines:

• Zero as the Center: Place zero in the middle of the number line.
• Positive Integers to the Right: Mark positive integers (1, 2, 3, …) to the right of zero at equal intervals.
• Negative Integers to the Left: Mark negative integers (-1, -2, -3, …) to the left of zero at equal intervals.

2.2. Using the Number Line for Comparison

The number line makes it easy to compare integers. Numbers to the right are always greater than numbers to the left. For example, 3 is greater than 1, and -1 is greater than -3. This visual comparison helps in understanding the order and magnitude of integers.

2.3. Arithmetic Operations on the Number Line

The number line can also be used to perform basic arithmetic operations with integers:

• Addition: To add a positive integer, move to the right on the number line. To add a negative integer, move to the left.
• Subtraction: To subtract a positive integer, move to the left on the number line. To subtract a negative integer, move to the right.

For example, to calculate 2 + 3 on the number line, start at 2 and move 3 units to the right, ending at 5. To calculate 2 – 3, start at 2 and move 3 units to the left, ending at -1.

2.4. Examples of Graphing Integers

Consider the following examples of graphing integers on a number line:

• To graph the integer 5, place a point on the number line at the position labeled 5.
• To graph the integer -4, place a point on the number line at the position labeled -4.
• To show the addition -2 + 5, start at -2 and move 5 units to the right, ending at 3.

The number line provides a visual and intuitive way to understand integers and their operations. It is a valuable tool for learners of all ages to grasp the concept of positive and negative numbers.

3. Integer Operations

Integer operations involve the basic arithmetic functions applied to integers. These operations include addition, subtraction, multiplication, and division. Each operation has specific rules that must be followed to ensure accurate results. Understanding these rules is crucial for performing mathematical calculations and solving problems involving integers.

3.1. Basic Arithmetic Operations

The four basic arithmetic operations are:

• Addition: Combining two or more integers to find their sum.
• Subtraction: Finding the difference between two integers.
• Multiplication: Finding the product of two or more integers.
• Division: Splitting an integer into equal parts.

3.2. Rules for Integer Operations

Each arithmetic operation has its own set of rules that dictate how to handle positive and negative integers:

• Addition Rules:
  • Adding two positive integers results in a positive integer.
  • Adding two negative integers results in a negative integer.
  • Adding a positive and a negative integer involves finding the difference between their absolute values and using the sign of the integer with the larger absolute value.
• Subtraction Rules:
  • Subtracting a positive integer is the same as adding a negative integer.
  • Subtracting a negative integer is the same as adding a positive integer.
• Multiplication Rules:
  • Multiplying two positive integers results in a positive integer.
  • Multiplying two negative integers results in a positive integer.
  • Multiplying a positive and a negative integer results in a negative integer.
• Division Rules:
  • Dividing two positive integers results in a positive integer.
  • Dividing two negative integers results in a positive integer.
  • Dividing a positive and a negative integer results in a negative integer.

3.3. Examples of Integer Operations

Let’s look at some examples to illustrate these rules:

• Addition:
  • 5 + 3 = 8 (positive + positive = positive)
  • (-5) + (-3) = -8 (negative + negative = negative)
  • 5 + (-3) = 2 (positive + negative = positive, since 5 > 3)
  • (-5) + 3 = -2 (negative + positive = negative, since 5 > 3)
• Subtraction:
  • 5 – 3 = 2 (positive – positive = positive)
  • 5 – (-3) = 5 + 3 = 8 (positive – negative = positive + positive)
  • (-5) – 3 = -5 + (-3) = -8 (negative – positive = negative + negative)
  • (-5) – (-3) = -5 + 3 = -2 (negative – negative = negative + positive)
• Multiplication:
  • 5 × 3 = 15 (positive × positive = positive)
  • (-5) × (-3) = 15 (negative × negative = positive)
  • 5 × (-3) = -15 (positive × negative = negative)
• Division:
  • 15 ÷ 3 = 5 (positive ÷ positive = positive)
  • (-15) ÷ (-3) = 5 (negative ÷ negative = positive)
  • 15 ÷ (-3) = -5 (positive ÷ negative = negative)

3.4. Order of Operations

When performing multiple operations in a single expression, it’s important to follow the order of operations, often remembered by the acronym PEMDAS:

1. Parentheses
2. Exponents
3. Multiplication and Division (from left to right)
4. Addition and Subtraction (from left to right)

For example, in the expression 2 + 3 × 4, multiplication is performed before addition:

2 + 3 × 4 = 2 + 12 = 14

Understanding and applying these rules ensures accuracy in mathematical calculations involving integers.

4. Addition of Integers

Adding integers is a fundamental arithmetic operation that combines two or more integers to find their sum. The process of adding integers can result in an increase or decrease in value, depending on whether the integers are positive or negative. Mastering the rules for adding integers is essential for performing more complex mathematical calculations.

4.1. Rules for Adding Integers

The rules for adding integers depend on the signs of the integers being added:

• Adding Integers with the Same Sign:
  • If both integers are positive, add their absolute values and the result is positive.
  • If both integers are negative, add their absolute values and the result is negative.
• Adding Integers with Different Signs:
  • Find the difference between the absolute values of the integers.
  • Assign the sign of the integer with the larger absolute value to the result.

4.2. Examples of Adding Integers

Let’s illustrate these rules with some examples:

• Adding Positive Integers:
  • 3 + 5 = 8 (Both integers are positive, so add them directly.)
• Adding Negative Integers:
  • (-3) + (-5) = -8 (Both integers are negative, so add their absolute values and make the result negative.)
• Adding Integers with Different Signs:
  • (-7) + 4 = -3 (The absolute values are 7 and 4. The difference is 3. Since 7 has a larger absolute value and is negative, the result is negative.)
  • 7 + (-4) = 3 (The absolute values are 7 and 4. The difference is 3. Since 7 has a larger absolute value and is positive, the result is positive.)

4.3. Using a Number Line for Addition

A number line provides a visual aid for understanding integer addition. Here’s how to use it:

1. Start at Zero: Begin at zero on the number line.
2. Move for the First Integer: Move to the position of the first integer.
3. Add Positive Integers: Move to the right for positive integers.
4. Add Negative Integers: Move to the left for negative integers.

Example:

• To calculate 3 + (-5) using a number line:
  1. Start at 0.
  2. Move 3 units to the right to reach 3.
  3. From 3, move 5 units to the left to reach -2.
  4. Therefore, 3 + (-5) = -2.

4.4. Practical Applications

Adding integers has many practical applications in everyday life, such as:

• Finance: Calculating bank balances (deposits and withdrawals).
• Temperature: Determining temperature changes (increases and decreases).
• Altitude: Measuring changes in elevation (climbing up or down).

Understanding the rules and methods for adding integers is crucial for mastering arithmetic and solving real-world problems.

5. Subtraction of Integers

Subtracting integers involves finding the difference between two or more integers. This operation can result in an increase or decrease in value, depending on the signs of the integers. Understanding the rules for subtraction is crucial for accurate calculations.

5.1. Rules for Subtracting Integers

The primary rule for subtracting integers is to convert the subtraction problem into an addition problem. This is done by changing the sign of the integer being subtracted (the subtrahend) and then adding it to the other integer (the minuend).

• Rule: a – b = a + (-b)

This rule applies regardless of whether a and b are positive or negative.

5.2. Examples of Subtracting Integers

Let’s illustrate the rule with some examples:

• Subtracting a Positive Integer:
  • 5 – 3 = 5 + (-3) = 2 (Change the sign of 3 to -3 and add it to 5.)
• Subtracting a Negative Integer:
  • 5 – (-3) = 5 + 3 = 8 (Change the sign of -3 to 3 and add it to 5.)
• Subtracting from a Negative Integer:
  • (-5) – 3 = (-5) + (-3) = -8 (Change the sign of 3 to -3 and add it to -5.)
  • (-5) – (-3) = (-5) + 3 = -2 (Change the sign of -3 to 3 and add it to -5.)

5.3. Using a Number Line for Subtraction

A number line can visually represent integer subtraction:

1. Start at the First Integer: Begin at the position of the first integer (minuend) on the number line.
2. Subtract Positive Integers: Move to the left for positive integers (subtracting).
3. Subtract Negative Integers: Move to the right for negative integers (subtracting a negative is like adding).

Example:

• To calculate 2 – (-3) using a number line:
  1. Start at 2.
  2. Since you are subtracting -3, move 3 units to the right (because subtracting a negative is the same as adding).
  3. You end at 5.
  4. Therefore, 2 – (-3) = 5.

5.4. Practical Applications

Subtracting integers is used in various real-world scenarios, including:

• Finance: Calculating profit or loss (revenue minus expenses).
• Temperature: Finding the difference in temperature between two points in time.
• Sports: Determining point differences in games.

Mastering the rules of integer subtraction is essential for solving mathematical problems and understanding real-world applications.

6. Multiplication of Integers

Multiplying integers involves finding the product of two or more integers. The rules for multiplication depend on the signs of the integers being multiplied. Understanding these rules is crucial for accurate calculations.

6.1. Rules for Multiplying Integers

The rules for multiplying integers are as follows:

• Positive × Positive = Positive:
  • When multiplying two positive integers, the result is always positive.
• Negative × Negative = Positive:
  • When multiplying two negative integers, the result is also positive.
• Positive × Negative = Negative:
  • When multiplying a positive integer by a negative integer, the result is negative.
• Negative × Positive = Negative:
  • When multiplying a negative integer by a positive integer, the result is also negative.

In summary:

• Same signs result in a positive product.
• Different signs result in a negative product.

6.2. Examples of Multiplying Integers

Let’s look at some examples to illustrate these rules:

• Positive × Positive:
  • 3 × 4 = 12
• Negative × Negative:
  • (-3) × (-4) = 12
• Positive × Negative:
  • 3 × (-4) = -12
• Negative × Positive:
  • (-3) × 4 = -12

6.3. Multiplying More Than Two Integers

When multiplying more than two integers, multiply the first two, then multiply the result by the next integer, and so on. The sign of the final product depends on the number of negative integers:

• If there is an even number of negative integers, the product is positive.
• If there is an odd number of negative integers, the product is negative.

Example:

• (-2) × 3 × (-1) × (-2) = -12 (Three negative integers, so the product is negative)
• (-2) × 3 × (-1) × 2 = 12 (Two negative integers, so the product is positive)

6.4. Practical Applications

Multiplication of integers is used in various real-world scenarios, including:

• Finance: Calculating total costs or revenue (e.g., if you lose $5 per day for 3 days, you’ve lost -5 × 3 = -$15).
• Physics: Calculating distance, velocity, and acceleration.
• Computer Science: Performing calculations in programming.

Understanding the rules for multiplying integers is crucial for accurate calculations and problem-solving in mathematics and real-world applications.

7. Division of Integers

Dividing integers involves splitting one integer into equal parts or groups. The rules for division, like multiplication, depend on the signs of the integers being divided. Understanding these rules is crucial for accurate calculations.

7.1. Rules for Dividing Integers

The rules for dividing integers are similar to those for multiplication:

• Positive ÷ Positive = Positive:
  • When dividing two positive integers, the result is always positive.
• Negative ÷ Negative = Positive:
  • When dividing two negative integers, the result is also positive.
• Positive ÷ Negative = Negative:
  • When dividing a positive integer by a negative integer, the result is negative.
• Negative ÷ Positive = Negative:
  • When dividing a negative integer by a positive integer, the result is also negative.

In summary:

• Same signs result in a positive quotient.
• Different signs result in a negative quotient.

7.2. Examples of Dividing Integers

Let’s illustrate these rules with some examples:

• Positive ÷ Positive:
  • 12 ÷ 3 = 4
• Negative ÷ Negative:
  • (-12) ÷ (-3) = 4
• Positive ÷ Negative:
  • 12 ÷ (-3) = -4
• Negative ÷ Positive:
  • (-12) ÷ 3 = -4

7.3. Division with Remainders

In some cases, division of integers may result in a remainder. The quotient is the integer result of the division, and the remainder is the amount left over.

Example:

• 14 ÷ 3 = 4 with a remainder of 2. This can be written as 14 = 3 × 4 + 2.
• (-14) ÷ 3 = -4 with a remainder of -2. This can be written as -14 = 3 × (-4) + (-2).

7.4. Practical Applications

Division of integers is used in various real-world scenarios, including:

• Finance: Splitting costs or revenue equally among individuals.
• Cooking: Adjusting recipe quantities.
• Computer Science: Performing calculations in programming.

Understanding the rules for dividing integers is crucial for accurate calculations and problem-solving in mathematics and real-world applications.

8. Properties of Integers

Integers, like other number systems, follow several important properties that govern how they behave under different operations. These properties are fundamental to understanding and working with integers effectively.

8.1. Closure Property

The closure property states that performing an operation on integers within the set of integers will always result in another integer.

• Addition: If a and b are integers, then a + b is also an integer.
• Subtraction: If a and b are integers, then a – b is also an integer.
• Multiplication: If a and b are integers, then a × b is also an integer.
• Division: The closure property does not hold for division. If a and b are integers, a ÷ b is not always an integer (e.g., 5 ÷ 2 = 2.5, which is not an integer).

8.2. Associative Property

The associative property states that the grouping of integers in addition and multiplication does not affect the result.

• Addition: a + (b + c) = (a + b) + c
• Multiplication: a × (b × c) = (a × b) × c

Example:

• Addition: 2 + (3 + 4) = 2 + 7 = 9 and (2 + 3) + 4 = 5 + 4 = 9
• Multiplication: 2 × (3 × 4) = 2 × 12 = 24 and (2 × 3) × 4 = 6 × 4 = 24

8.3. Commutative Property

The commutative property states that the order of integers in addition and multiplication does not affect the result.

• Addition: a + b = b + a
• Multiplication: a × b = b × a

Example:

• Addition: 2 + 3 = 5 and 3 + 2 = 5
• Multiplication: 2 × 3 = 6 and 3 × 2 = 6

8.4. Distributive Property

The distributive property states how multiplication interacts with addition.

• a × (b + c) = (a × b) + (a × c)

Example:

• 2 × (3 + 4) = 2 × 7 = 14 and (2 × 3) + (2 × 4) = 6 + 8 = 14

8.5. Identity Property

The identity property defines the existence of identity elements for addition and multiplication.

• Additive Identity: The additive identity is 0. For any integer a, a + 0 = a.
• Multiplicative Identity: The multiplicative identity is 1. For any integer a, a × 1 = a.

8.6. Inverse Property

The inverse property defines the existence of inverse elements for addition and multiplication.

• Additive Inverse: For any integer a, there exists an additive inverse -a such that a + (-a) = 0.
• Multiplicative Inverse: The multiplicative inverse (reciprocal) exists for multiplication. For any integer a (except 0), there exists a multiplicative inverse 1/a such that a × (1/a) = 1. However, the multiplicative inverse of an integer is not always an integer itself.

8.7. Zero Property

The zero property states that any integer multiplied by zero results in zero.

• For any integer a, a × 0 = 0.

Understanding these properties is essential for performing algebraic manipulations, simplifying expressions, and solving equations involving integers.

9. FAQs on Integers

Here are some frequently asked questions about integers to help clarify any remaining doubts:

9.1. What are Integers in Math?

Integers in math are whole numbers (not fractions or decimals) that can be positive, negative, or zero. They include numbers like -3, -2, -1, 0, 1, 2, 3, and so on.

9.2. What are the Different Types of Integers?

There are three main types of integers:

• Positive Integers: Integers greater than zero (e.g., 1, 2, 3, …).
• Negative Integers: Integers less than zero (e.g., -1, -2, -3, …).
• Zero: The integer that is neither positive nor negative.

9.3. Can a Negative Number Be an Integer?

Yes, a negative number can be an integer as long as it is a whole number (no fractions or decimals). Examples include -5, -100, and -1000.

9.4. What are Consecutive Integers?

Consecutive integers are integers that follow each other in order. For example, 1, 2, 3, 4 are consecutive integers. Similarly, -3, -2, -1, 0 are also consecutive integers.

9.5. What is the Rule for Adding a Positive and Negative Integer?

When adding a positive and negative integer, find the difference between their absolute values and assign the sign of the integer with the larger absolute value to the result. For example, -7 + 4 = -3 (since 7 – 4 = 3 and 7 has a larger absolute value and is negative).

9.6. What are the Properties of Integers?

The major properties of integers include:

• Closure Property
• Associative Property
• Commutative Property
• Distributive Property
• Identity Property
• Inverse Property
• Zero Property

These properties govern how integers behave under different operations.

9.7. What are the Applications of Integers?

Integers are used in various real-world applications, including:

• Finance: Representing bank balances, debts, and profits/losses.
• Temperature: Measuring temperatures above and below zero.
• Altitude: Representing heights above and below sea level.
• Computer Science: Performing calculations and representing data.

9.8. Why is the Set of Integers Called Z?

The set of integers is denoted by the letter Z, which comes from the German word “Zahlen,” meaning numbers.

9.9. What is a Negative Integer?

A negative integer is an integer that is less than zero and has a negative sign before it. Examples include -1, -2, -3, -10, and -100.

9.10. What is a Positive Integer?

A positive integer is an integer that is greater than zero and has a positive sign (or no sign) before it. Examples include 1, 2, 3, 10, and 100.

Do you still have questions about integers or any other math topics? Don’t hesitate to ask! At WHAT.EDU.VN, we provide a free platform where you can ask any question and receive quick, accurate answers from knowledgeable experts.

We understand the challenges of finding reliable, cost-free information. That’s why we’ve created a community where everyone can benefit from shared knowledge. Whether you’re a student tackling homework or a curious individual seeking answers, we’re here to help.

Our services are designed to be user-friendly and accessible to all. We ensure that information is easy to understand and presented in a clear, concise manner. Plus, our team is committed to updating content regularly to keep you informed with the latest and most accurate information.

Join us today at WHAT.EDU.VN and experience the convenience of free, expert advice at your fingertips.

Have questions? Get free answers on WHAT.EDU.VN!

Contact us:

Address: 888 Question City Plaza, Seattle, WA 98101, United States

WhatsApp: +1 (206) 555-7890

Website: what.edu.vn