What Is A Line Of Symmetry? Explore symmetry lines, mirror lines, and axis of symmetry with WHAT.EDU.VN and learn how to identify symmetry in shapes. Uncover the secrets of symmetrical figures! Want to delve deeper? Ask your questions on WHAT.EDU.VN for free expert answers, improving your understanding of geometric symmetry and reflective symmetry.
1. Understanding the Line of Symmetry
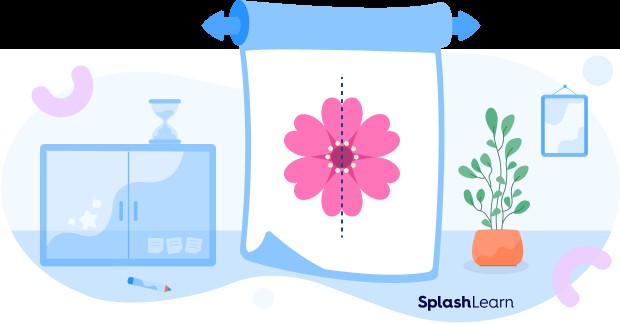
In mathematics, a line of symmetry, also known as an axis of symmetry or a mirror line, is an imaginary line that divides a shape or object into two identical halves. Each half is a mirror reflection of the other. If you were to fold the shape along this line, the two halves would perfectly overlap. This division creates balanced and identical parts, exhibiting mirror symmetry. For example, a heart shape can be split evenly down the middle, showing symmetry.
2. Definition of a Line of Symmetry Explained
A line of symmetry is the line that passes exactly through the center of a shape or object, dividing it into two mirror images. This line can be thought of as a “folding line,” where both halves match perfectly when folded. According to geometry resources, a shape possesses line symmetry if there exists a line that separates the shape into two congruent halves. In simpler terms, each point on one side of the line has a corresponding point on the opposite side, equidistant from the line. This helps students understand the balance and mirror effect.
2.1. Importance of Equal Parts
The concept of “equal parts” is vital when understanding lines of symmetry. Both sides of the line must be congruent—identical in size and shape. This means that the distance from any point on one side to the line of symmetry is exactly the same as the distance from its corresponding point on the other side to the line. Recognizing these equal parts helps identify symmetry.
2.2. The Mirror Line Concept
Often referred to as a “mirror line,” the line of symmetry creates an image that is a precise reflection. Imagine holding a mirror along the line; what you see in the mirror on one side is exactly what you see on the other. This reflection is a fundamental property of symmetry, making it visually apparent. Symmetry in art and design utilizes this mirror effect to create aesthetically pleasing compositions.
3. Symmetric vs. Asymmetric Figures
3.1. Defining Symmetric Figures
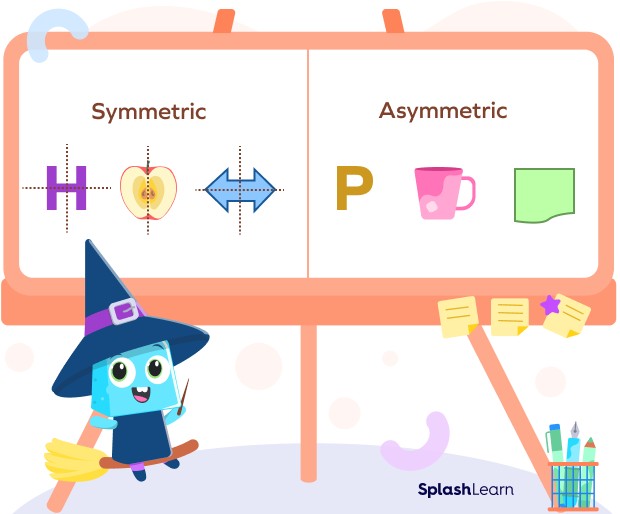
Symmetric figures are shapes or objects that can be divided into two identical halves by a line. These shapes exhibit balance and harmony. Examples include circles, squares, and certain letters like “A,” “H,” and “O.” Symmetric figures are visually pleasing because of their balanced proportions.
3.2. Understanding Asymmetric Figures
Asymmetric figures are shapes or objects that cannot be divided into two identical halves by any single line. These shapes lack balance and harmony in their form. Examples include scalene triangles, irregular polygons, and letters like “P,” “Q,” and “R.” Asymmetry is common in nature and can create dynamic and interesting designs.
3.3. Examples of Symmetric and Asymmetric Shapes
| Shape | Symmetric? | Lines of Symmetry | Notes |
|---|---|---|---|
| Circle | Yes | Infinite | Any line passing through the center is a line of symmetry. |
| Square | Yes | 4 | Two diagonal lines and two lines through the middle of opposite sides. |
| Rectangle | Yes | 2 | Lines through the middle of opposite sides. |
| Equilateral Triangle | Yes | 3 | Each line runs from a vertex to the midpoint of the opposite side. |
| Isosceles Triangle | Yes | 1 | One line runs from the vertex angle to the midpoint of the base. |
| Scalene Triangle | No | 0 | No lines of symmetry. |
| Heart | Yes | 1 | Vertical line through the cleft. |
| Parallelogram | No | 0 | No lines of symmetry unless it is a rhombus or rectangle. |
| Kite | Yes | 1 | One line runs along the longer diagonal. |
| Irregular Polygon | No | 0 | Does not have any equal sides or angles. |


4. Types of Lines of Symmetry
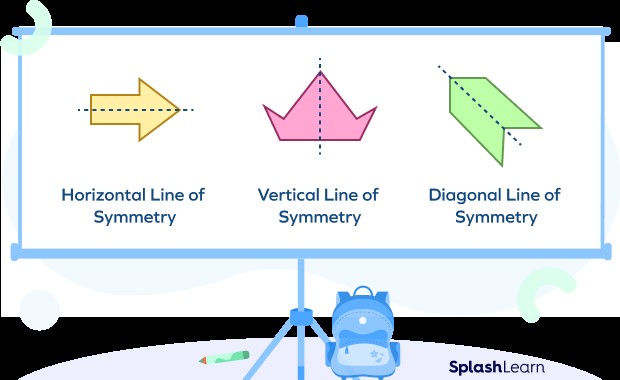
4.1. Horizontal Line of Symmetry
A horizontal line of symmetry divides an object into two identical halves from left to right. This means the top half of the object mirrors the bottom half. Letters like “B,” “C,” “D,” “E,” “H,” “I,” “K,” “O,” and “X” exhibit horizontal symmetry. A rectangle cut horizontally shows this symmetry.
4.2. Vertical Line of Symmetry
A vertical line of symmetry divides an object into two identical halves from top to bottom. In this case, the left half of the object mirrors the right half. Letters like “A,” “H,” “I,” “M,” “O,” “T,” “U,” “V,” “W,” “X,” and “Y” show vertical symmetry. A standing human figure is an excellent example of vertical symmetry.
4.3. Diagonal Line of Symmetry
A diagonal line of symmetry divides an object into two identical halves at an angle. This type of symmetry is found in shapes like diamonds and some rhombuses. Letters like “Z” do not have any lines of symmetry, while others, like “X,” may have diagonal lines of symmetry in addition to horizontal and vertical lines.
4.4. Examples of Symmetry in Different Shapes
| Shape | Horizontal Symmetry | Vertical Symmetry | Diagonal Symmetry |
|---|---|---|---|
| Square | Yes | Yes | Yes |
| Rectangle | Yes | Yes | No |
| Circle | Yes | Yes | Yes |
| Diamond/Rhombus | No | No | Yes |
| Isosceles Triangle | No | Yes | No |
| Equilateral Triangle | No | Yes | No |
| Kite | No | Yes | No |
| Letter “H” | Yes | Yes | No |
| Letter “A” | No | Yes | No |
| Letter “B” | Yes | No | No |
| Letter “X” | Yes | Yes | Yes |
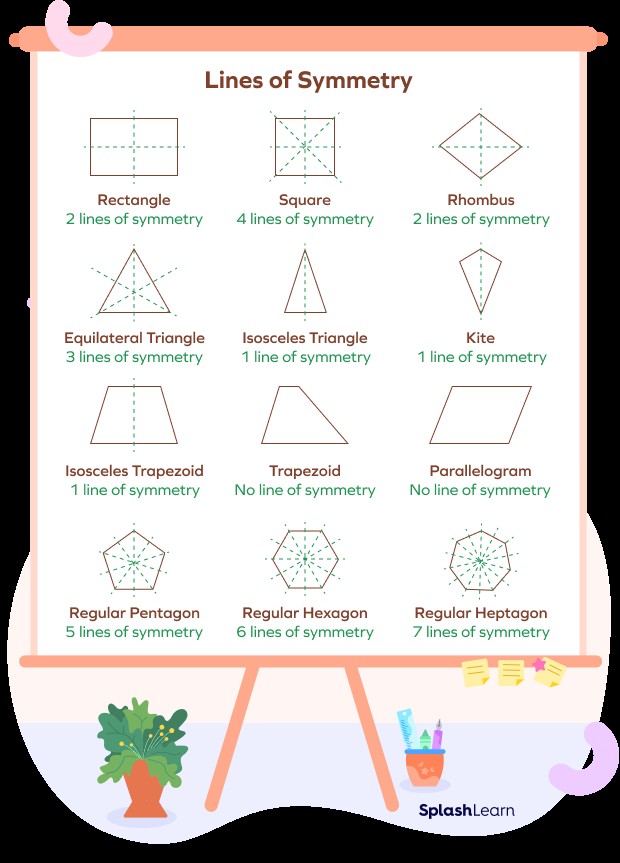
5. Number of Lines of Symmetry in a Shape
A shape can have multiple lines of symmetry depending on its structure and properties. A shape with one line of symmetry has only one way to be divided into identical parts, while shapes with multiple lines of symmetry offer several ways to achieve this. The lines can be horizontal, vertical, or diagonal.
5.1. Shapes with One Line of Symmetry
Shapes with only one line of symmetry include isosceles triangles, kites, and certain irregular polygons. These shapes have a unique balance that is only achievable through one specific division. This single line reflects the shape perfectly.
5.2. Shapes with Multiple Lines of Symmetry
Shapes with multiple lines of symmetry exhibit a higher degree of balance and regularity. Examples include squares (4 lines), rectangles (2 lines), and equilateral triangles (3 lines). A circle has infinite lines of symmetry because any line passing through its center divides it into identical halves.
5.3. Examples of Shapes and Their Lines of Symmetry
| Shape | Number of Lines of Symmetry | Type of Lines |
|---|---|---|
| Circle | Infinite | Any line through the center |
| Square | 4 | Horizontal, Vertical, and two Diagonal lines |
| Rectangle | 2 | Horizontal and Vertical lines |
| Equilateral Triangle | 3 | Lines from each vertex to the midpoint of the opposite side |
| Isosceles Triangle | 1 | Line from vertex angle to midpoint of the base |
| Kite | 1 | Line along the longer diagonal |
| Regular Pentagon | 5 | Lines from each vertex to the midpoint of the opposite side |
| Regular Hexagon | 6 | Lines through opposite vertices and midpoints of opposite sides |
6. Line of Symmetry in Geometry
In geometry, the axis of symmetry is a fundamental concept used to describe the balance and proportions of shapes. Two-dimensional geometric shapes, such as triangles, squares, and circles, can have one or more lines of symmetry. Understanding these lines helps in analyzing and classifying geometric figures.
6.1. Symmetry in Two-Dimensional Shapes
Two-dimensional shapes are flat figures that exist on a plane. These shapes can exhibit different types of symmetry, including reflectional (line) symmetry and rotational symmetry. Line symmetry, as we’ve discussed, involves dividing the shape into identical halves.
6.2. Common Geometric Shapes and Their Symmetry
| Shape | Lines of Symmetry |
|---|---|
| Circle | Infinite |
| Square | 4 |
| Rectangle | 2 |
| Triangle | 0, 1, or 3 |
| Parallelogram | 0 |
| Rhombus | 2 |
6.3. Examples of Lines of Symmetry in Geometric Shapes
- Circle: Infinite lines of symmetry.
- Square: Four lines of symmetry (horizontal, vertical, and two diagonals).
- Rectangle: Two lines of symmetry (horizontal and vertical).
- Equilateral Triangle: Three lines of symmetry.
- Isosceles Triangle: One line of symmetry.
7. Real-World Examples of Lines of Symmetry
Symmetry isn’t just a mathematical concept; it’s also a pervasive feature of the world around us. From nature to architecture, lines of symmetry create balance and harmony in various forms. Recognizing these examples can help appreciate the beauty and order in the world.
7.1. Symmetry in Nature
Nature is replete with examples of symmetry. Butterflies, with their mirrored wings, are a classic illustration. Leaves, flowers, and even the human body exhibit approximate symmetry. These natural symmetries often serve functional purposes, such as balance and camouflage.
7.2. Symmetry in Architecture
Architects often employ symmetry to create visually appealing and stable structures. Buildings like the Taj Mahal and the White House exhibit strong symmetry, with balanced proportions on either side of a central axis. Symmetry in architecture conveys a sense of order and stability.
7.3. Symmetry in Everyday Objects
Many everyday objects are designed with symmetry in mind. Cars, furniture, and appliances often have symmetrical designs for both aesthetic and functional reasons. A symmetrical design can provide balance, ease of use, and visual appeal.
8. How to Find a Line of Symmetry
Finding a line of symmetry involves visually inspecting or physically manipulating a shape to determine if it can be divided into two identical halves. This can be done through folding, drawing lines, or using geometric tools. The goal is to find a line that creates a mirror reflection.
8.1. Visual Inspection
The first step in finding a line of symmetry is often a visual inspection. Look at the shape and try to imagine a line that would divide it into two identical halves. This method is useful for simple shapes like circles, squares, and rectangles.
8.2. Folding Method
The folding method involves physically folding the shape along a potential line of symmetry. If the two halves match perfectly, then the fold line is a line of symmetry. This method is particularly effective for hands-on learning and verifying visual assessments.
8.3. Using Geometric Tools
Geometric tools like rulers and compasses can also be used to find lines of symmetry. By measuring distances and angles, you can accurately determine if a line divides a shape into congruent halves. This method is especially useful for complex shapes where visual inspection and folding may be insufficient.
9. Examples of Lines of Symmetry in Letters
The letters of the alphabet provide a simple and accessible way to understand lines of symmetry. Different letters exhibit horizontal, vertical, or no symmetry at all. Examining these letters can reinforce the concept of symmetry in an easily recognizable context.
9.1. Letters with Vertical Symmetry
Letters with vertical symmetry can be divided into two identical halves along a vertical line. Examples include A, H, I, M, O, T, U, V, W, X, and Y. These letters have a mirror image when reflected across the vertical axis.
9.2. Letters with Horizontal Symmetry
Letters with horizontal symmetry can be divided into two identical halves along a horizontal line. Examples include B, C, D, E, H, I, K, O, and X. These letters have a mirror image when reflected across the horizontal axis.
9.3. Letters with No Symmetry
Some letters of the alphabet have no lines of symmetry. These letters cannot be divided into two identical halves by any single line. Examples include F, G, J, L, N, P, Q, R, S, and Z.
9.4. Table of Letter Symmetries
| Letter | Vertical Symmetry | Horizontal Symmetry |
|---|---|---|
| A | Yes | No |
| B | No | Yes |
| C | No | Yes |
| D | No | Yes |
| E | No | Yes |
| F | No | No |
| G | No | No |
| H | Yes | Yes |
| I | Yes | Yes |
| J | No | No |
| K | No | Yes |
| L | No | No |
| M | Yes | No |
| N | No | No |
| O | Yes | Yes |
| P | No | No |
| Q | No | No |
| R | No | No |
| S | No | No |
| T | Yes | No |
| U | Yes | No |
| V | Yes | No |
| W | Yes | No |
| X | Yes | Yes |
| Y | Yes | No |
| Z | No | No |
10. Solved Examples on Line of Symmetry
To solidify your understanding, let’s work through some solved examples that illustrate how to identify and apply the concept of lines of symmetry.
Example 1: How many lines of symmetry does the given figure have?
Solution: The given figure only has one line of symmetry.
Example 2: Identify whether the given line of symmetry is a vertical, horizontal, or diagonal line of symmetry.
Solution: The given line is a vertical line of symmetry.
Example 3: Write three capital letters in the English alphabet that have no lines of symmetry?
Solution: The three letters in the English alphabet that have no lines of symmetry are P, G, and J.
Example 4: Write three capital letters in the English alphabet with horizontal and vertical lines of symmetry.
Solution: The English alphabets with horizontal and vertical lines of symmetry are H, I, and O.
11. Why is Understanding Lines of Symmetry Important?
Understanding lines of symmetry is crucial for various reasons, impacting mathematics, art, design, and everyday problem-solving. This fundamental concept enhances visual skills, logical thinking, and spatial reasoning.
11.1. Enhancing Mathematical Skills
Lines of symmetry are a basic concept in geometry, providing a foundation for more advanced topics like transformations and tessellations. By understanding symmetry, students can better grasp geometric principles and solve complex problems.
11.2. Applications in Art and Design
Symmetry plays a significant role in art and design. Artists and designers use symmetry to create balanced, harmonious, and visually appealing compositions. Understanding symmetry allows for intentional use of balance and proportion.
11.3. Improving Problem-Solving Abilities
Recognizing and identifying lines of symmetry improves problem-solving abilities by enhancing visual and spatial reasoning skills. Symmetry helps break down complex shapes into simpler, manageable parts, aiding in analysis and understanding.
12. Practice Problems on Line of Symmetry
Test your knowledge with these practice problems.
- Draw all the lines of symmetry for a square.
- Does a parallelogram have any lines of symmetry?
- How many lines of symmetry does a regular hexagon have?
- Identify whether the letter “M” has vertical or horizontal symmetry.
- Draw a shape that has exactly one line of symmetry.
- Determine if the following shape is symmetrical and, if so, draw the line(s) of symmetry.
13. Frequently Asked Questions (FAQs) About Lines of Symmetry
Still have questions? Here are some frequently asked questions about lines of symmetry to clarify any lingering doubts.
13.1. What is the maximum number of lines of symmetry in an object?
The maximum number of lines of symmetry depends on the shape or figure. For example, an isosceles triangle has one line of symmetry, the rectangle has two lines of symmetry, and the circle has an infinite line of symmetry.
13.2. Are there shapes that have no lines of symmetry?
Yes, shapes that are irregular and do not resemble each other when divided into two parts are called asymmetric. Such shapes do not have a line of symmetry. A scalene triangle, a parallelogram, and a trapezium are examples of shapes that have no lines of symmetry.
13.3. How do you find the line of symmetry for a shape?
Fold the shape so that one half is identical to the other half. The line along which you have folded can be called a line of symmetry. There can be more than one such line or line of symmetry.
13.4. How many lines of symmetry does a regular polygon have?
In a regular polygon, all sides and angles are equal. If it has “n” number of sides, it will also have “n” number of lines of symmetry. For example, a square with four equal sides has four lines of symmetry, and a regular pentagon has five lines of symmetry.
14. Conclusion
Lines of symmetry are a fundamental concept in mathematics and design, influencing how we perceive balance and harmony in shapes and objects. Understanding this concept enhances problem-solving skills, visual literacy, and appreciation for the world around us. If you’re eager to learn more or have further questions, visit WHAT.EDU.VN for expert answers and free educational resources. Don’t hesitate to ask—our community is here to help you explore and understand the world of symmetry and beyond!
14.1. Still Have Questions?
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: WHAT.EDU.VN
14.2. Ready to Learn More?
Dive deeper into mathematics and design! Visit what.edu.vn today to ask questions and discover a world of knowledge.