What Is A Natural Number? This comprehensive guide from WHAT.EDU.VN will explain natural numbers, their properties, and how they differ from other number sets, offering clear explanations and practical examples. Explore the world of counting numbers, positive integers, and discover the essence of elementary number theory, including arithmetic.
1. Understanding Natural Numbers: The Basics
Natural numbers are the foundation of mathematics, serving as the building blocks for more complex number systems. But precisely what is a natural number? Simply put, natural numbers are the positive whole numbers we use for counting. They start at 1 and extend infinitely. They are also sometimes called “counting numbers” because they are the numbers we use when we first learn to count objects.
1.1. Natural Number Definition Explained
A natural number is a positive integer, meaning it’s a whole number greater than zero. The set of natural numbers includes 1, 2, 3, 4, 5, and so on, extending to infinity. These numbers are fundamental to arithmetic and are used extensively in everyday life, from counting items to performing basic calculations.
1.2. Natural Number Examples
To clarify the concept, here are a few examples of natural numbers:
- 5
- 27
- 143
- 1000
- 5,280
These examples illustrate that any positive whole number you can count is a natural number. Numbers such as -3, 0, 2.5, or √2 are not natural numbers because they are either negative, zero, fractions, or irrational.
1.3. Set of Natural Numbers: Representation
In mathematical notation, the set of natural numbers is often denoted by the symbol N. This set can be represented in several ways:
- Roster Form: N = {1, 2, 3, 4, 5, …}
- Set Builder Form: N = {x : x is an integer and x > 0}
These representations show that the set N includes all integers greater than zero, extending infinitely.
2. Key Characteristics of Natural Numbers
Natural numbers possess unique characteristics that distinguish them from other types of numbers. Understanding these properties is crucial for grasping their role in mathematics.
2.1. Smallest Natural Number Unveiled
The smallest natural number is 1. This is because natural numbers are counting numbers, and counting starts from 1. There is no natural number smaller than 1.
2.2. Odd and Even Natural Numbers
Natural numbers can be further categorized into odd and even numbers:
- Odd Natural Numbers: These are natural numbers not divisible by 2. The set of odd natural numbers is {1, 3, 5, 7, …}.
- Even Natural Numbers: These are natural numbers divisible by 2. The set of even natural numbers is {2, 4, 6, 8, …}.
Understanding the distinction between odd and even natural numbers is crucial in various mathematical concepts, such as number theory and modular arithmetic.
2.3. Prime and Composite Natural Numbers
Natural numbers can also be classified as prime or composite:
- Prime Numbers: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. Examples include 2, 3, 5, 7, 11, and so on.
- Composite Numbers: A composite number is a natural number greater than 1 that has at least one positive divisor other than 1 and itself. Examples include 4, 6, 8, 9, 10, and so on.
Prime numbers are fundamental in cryptography and other areas of advanced mathematics.
3. Natural Numbers vs. Whole Numbers: What’s the Difference?
It’s common to confuse natural numbers with whole numbers, but there is a key difference. Let’s explore the distinction between these two number sets.
3.1. Whole Numbers Explained
Whole numbers are a set of numbers that include all natural numbers plus zero. The set of whole numbers is represented as {0, 1, 2, 3, 4, …}. The primary difference between natural and whole numbers is the inclusion of zero in the set of whole numbers.
3.2. Natural Numbers and Whole Numbers: A Side-by-Side Comparison
To better understand the difference, consider the following comparison:
| Feature | Natural Numbers | Whole Numbers |
|---|---|---|
| Definition | Positive counting numbers | Positive counting numbers and zero |
| Set Representation | N = {1, 2, 3, 4, …} | W = {0, 1, 2, 3, 4, …} |
| Smallest Number | 1 | 0 |
| Inclusion of Zero | No | Yes |


This table clearly illustrates that every natural number is a whole number, but not every whole number is a natural number, because zero is a whole number but not a natural number.
3.3. Why is Zero Not a Natural Number?
Zero is not a natural number by definition. Natural numbers are used for counting, and counting typically starts from one. Zero represents the absence of quantity, so it doesn’t fit the concept of counting.
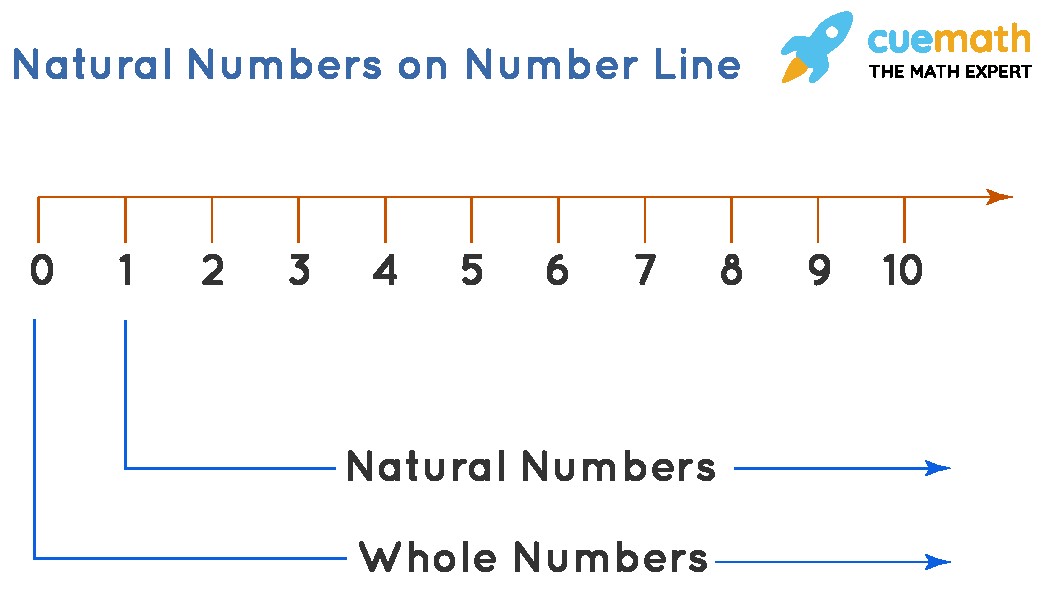
4. Visualizing Natural Numbers on a Number Line
A number line is a useful tool for visualizing numbers and their relationships. Let’s see how natural numbers are represented on a number line.
4.1. Natural Numbers on a Number Line: An Illustration
On a number line, natural numbers are represented as points starting from 1 and extending infinitely to the right. Each point corresponds to a natural number, with equal spacing between consecutive numbers.
4.2. Representing Whole Numbers on a Number Line
Whole numbers are represented similarly, but with an additional point at zero. The number line starts at 0 and extends infinitely to the right, with each point representing a whole number.
4.3. Using Number Lines for Basic Operations
Number lines can also be used to perform basic arithmetic operations with natural numbers, such as addition and subtraction. For example, to add 2 and 3, start at 2 on the number line and move 3 units to the right, ending at 5.
5. Properties of Natural Numbers: Essential Rules
Natural numbers follow certain properties under arithmetic operations. Understanding these properties is essential for solving mathematical problems.
5.1. Closure Property: Addition and Multiplication
The closure property states that the sum or product of two natural numbers is always a natural number.
- Addition: If a and b are natural numbers, then a + b is also a natural number. For example, 3 + 5 = 8, where 3, 5, and 8 are all natural numbers.
- Multiplication: If a and b are natural numbers, then a × b is also a natural number. For example, 4 × 6 = 24, where 4, 6, and 24 are all natural numbers.
5.2. Associative Property: Grouping Numbers
The associative property states that the way numbers are grouped in addition or multiplication does not change the result.
- Addition: a + (b + c) = (a + b) + c. For example, 2 + (3 + 4) = 2 + 7 = 9, and (2 + 3) + 4 = 5 + 4 = 9.
- Multiplication: a × (b × c) = (a × b) × c. For example, 2 × (3 × 4) = 2 × 12 = 24, and (2 × 3) × 4 = 6 × 4 = 24.
5.3. Commutative Property: Order Matters
The commutative property states that the order of numbers in addition or multiplication does not change the result.
- Addition: a + b = b + a. For example, 5 + 7 = 12 and 7 + 5 = 12.
- Multiplication: a × b = b × a. For example, 6 × 8 = 48 and 8 × 6 = 48.
5.4. Distributive Property: Combining Operations
The distributive property states how multiplication distributes over addition or subtraction.
- Multiplication over Addition: a × (b + c) = (a × b) + (a × c). For example, 2 × (3 + 4) = 2 × 7 = 14, and (2 × 3) + (2 × 4) = 6 + 8 = 14.
- Multiplication over Subtraction: a × (b – c) = (a × b) – (a × c). For example, 3 × (5 – 2) = 3 × 3 = 9, and (3 × 5) – (3 × 2) = 15 – 6 = 9.
Understanding these properties helps simplify calculations and solve mathematical problems more efficiently.
6. Real-World Applications of Natural Numbers
Natural numbers are not just abstract mathematical concepts; they have numerous real-world applications. Let’s explore some practical uses of natural numbers.
6.1. Counting and Measuring
The most basic application of natural numbers is in counting and measuring. Whether you’re counting the number of apples in a basket or measuring the length of a room, you’re using natural numbers.
6.2. Data Analysis and Statistics
Natural numbers are used extensively in data analysis and statistics. They are used to count occurrences, measure frequencies, and analyze patterns in data sets.
6.3. Computer Science and Programming
In computer science, natural numbers are used to index arrays, count iterations in loops, and perform various other computational tasks. They are fundamental to algorithms and data structures.
6.4. Finance and Accounting
Natural numbers are used in finance and accounting to count money, track transactions, and calculate profits and losses. They are essential for managing budgets and financial statements.
7. Natural Numbers and Other Number Systems
Natural numbers are part of a larger family of number systems. Let’s see how they relate to other types of numbers.
7.1. Integers: Including Negatives
Integers include all natural numbers, their negative counterparts, and zero. The set of integers is represented as {…, -3, -2, -1, 0, 1, 2, 3, …}. Integers extend the concept of numbers to include negative values.
7.2. Rational Numbers: Fractions and Decimals
Rational numbers are numbers that can be expressed as a fraction p/q, where p and q are integers and q is not zero. Rational numbers include natural numbers, integers, fractions, and terminating or repeating decimals.
7.3. Real Numbers: The Complete Set
Real numbers include all rational and irrational numbers. Irrational numbers are numbers that cannot be expressed as a fraction of two integers, such as √2 and π. Real numbers encompass all numbers on the number line.
8. Practice Questions and Examples
To solidify your understanding of natural numbers, let’s work through some practice questions and examples.
8.1. Example 1: Identifying Natural Numbers
Which of the following numbers are natural numbers: -4, 0, 1/2, 3, 7.5, 15?
Solution: The natural numbers are 3 and 15.
8.2. Example 2: Sum of First N Natural Numbers
Find the sum of the first 10 natural numbers.
Solution: The sum of the first n natural numbers is given by the formula: S = n(n + 1)/2. So, for n = 10, S = 10(10 + 1)/2 = 10(11)/2 = 55.
8.3. Example 3: Properties of Natural Numbers
Show that the closure property holds for addition with the natural numbers 2 and 8.
Solution: According to the closure property, if a and b are natural numbers, then a + b is also a natural number. In this case, a = 2 and b = 8. Therefore, a + b = 2 + 8 = 10, which is also a natural number.
9. Common Misconceptions About Natural Numbers
It’s common to have misconceptions about natural numbers. Let’s address some of the most common ones.
9.1. Zero is a Natural Number
One of the most common misconceptions is that zero is a natural number. By definition, natural numbers start at 1 and do not include zero. Zero is a whole number, but not a natural number.
9.2. Negative Numbers are Natural Numbers
Another misconception is that negative numbers are natural numbers. Natural numbers are positive integers only. Negative numbers are integers but not natural numbers.
9.3. Fractions and Decimals are Natural Numbers
Fractions and decimals are not natural numbers unless they are whole numbers. For example, 2.5 is a decimal, and 1/2 is a fraction; neither is a natural number.
10. Frequently Asked Questions (FAQs) About Natural Numbers
Here are some frequently asked questions about natural numbers to help clarify any remaining doubts.
10.1. What are Natural Numbers in Math?
Natural numbers are the positive integers used for counting, starting from 1 and extending infinitely. They are fundamental to arithmetic and are used extensively in various mathematical fields.
10.2. What is the Sum of the First 20 Natural Numbers?
The sum of the first n natural numbers is given by the formula: S = n(n + 1)/2. For n = 20, S = 20(20 + 1)/2 = 20(21)/2 = 210.
10.3. How Many Natural Numbers are There?
There are infinitely many natural numbers. The set of natural numbers starts at 1 and extends without end.
10.4. How are Natural Numbers Different from Integers?
Natural numbers are positive integers starting from 1, while integers include all positive and negative whole numbers, as well as zero. The main difference is that integers include negative numbers and zero, while natural numbers do not.
10.5. What are the Four Basic Properties of Natural Numbers?
The four basic properties of natural numbers are:
- Closure property
- Associative property
- Commutative property
- Distributive property
10.6. What is an Example of a Natural Number?
An example of a natural number is 7. It is a positive integer used for counting.
10.7. Is -5 a Natural Number?
No, -5 is not a natural number because it is a negative integer. Natural numbers are positive integers only.
10.8. Why are Natural Numbers Called Natural?
Natural numbers are called natural because they are the numbers that come “naturally” to us when we start counting. They are the most intuitive and basic form of numbers.
10.9. What are the First Ten Natural Numbers?
The first ten natural numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10.
10.10. How to Find the Sum of n Natural Numbers?
To find the sum of n natural numbers, use the formula: S = n(n + 1)/2, where n is the number of terms.
10.11. Are All Natural Numbers Integers?
Yes, all natural numbers are integers because integers include all positive and negative whole numbers, as well as zero, and natural numbers are a subset of positive integers.
10.12. Write the Next Three Natural Numbers After 999.
The next three natural numbers after 999 are 1000, 1001, and 1002.
10.13. What is the Greatest Natural Number?
There is no greatest natural number because the set of natural numbers extends infinitely.
10.14. Is 1 a Natural Number?
Yes, 1 is the smallest natural number.
10.15. Where do Natural Numbers Start From?
Natural numbers start from 1 and extend to infinity.
Conclusion: Mastering Natural Numbers
Understanding what is a natural number is fundamental to mathematics. They are the building blocks of arithmetic and are used extensively in various fields, from counting and measuring to computer science and finance. By understanding their properties and how they relate to other number systems, you can build a strong foundation for more advanced mathematical concepts.
Do you have more questions about natural numbers or any other math topics? Visit WHAT.EDU.VN to ask your questions and get free answers from our community of experts. Our platform offers a convenient and accessible way to get the help you need, whether you’re a student, a professional, or just curious about the world around you.
We understand that finding answers to your questions can sometimes be challenging. You might not know who to ask, where to look, or you might be concerned about the cost of getting help. That’s why WHAT.EDU.VN is here to provide you with a free and easy-to-use platform where you can ask any question and receive prompt and accurate answers.
Here’s how WHAT.EDU.VN helps you:
- Free Question Answering: Ask any question and get answers without any cost.
- Quick Responses: Our community of experts is dedicated to providing timely and accurate answers.
- Easy-to-Understand Explanations: We provide clear and concise explanations that are easy to understand for everyone.
- Community Support: Connect with other users to exchange knowledge and insights.
Ready to get started?
Visit WHAT.EDU.VN today and ask your question. Let us help you find the answers you need.
Contact Us:
- Address: 888 Question City Plaza, Seattle, WA 98101, United States
- WhatsApp: +1 (206) 555-7890
- Website: what.edu.vn
Don’t hesitate—your answers are just a click away!
