The numerator is a fundamental concept in mathematics, representing a key component of fractions; related terms include the denominator, fractions, and division. WHAT.EDU.VN explains the numerator in a clear and concise manner. If you need help grasping number relationships, fraction components, or basic math terms, keep reading for insight! For more in-depth mathematical insights, explore our comprehensive resources and get all your questions answered on WHAT.EDU.VN
1. What is a Numerator?
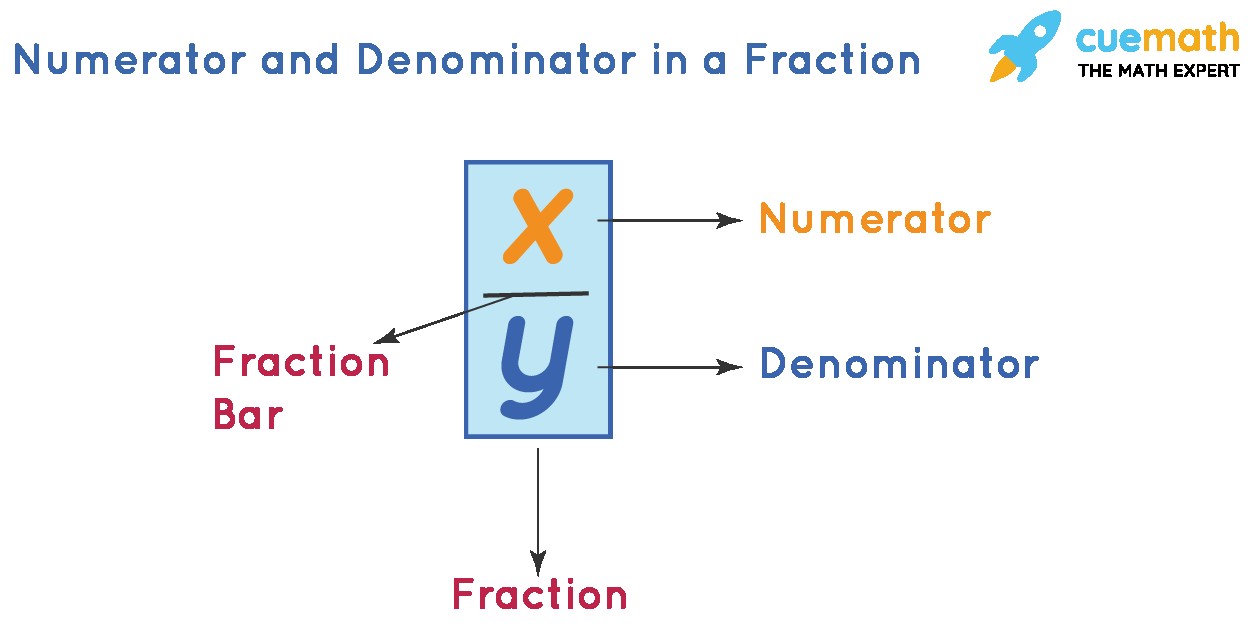
In mathematics, a fraction consists of two primary components: the numerator and the denominator. The numerator is defined as the number positioned above the fraction bar, also known as the vinculum. The denominator resides below the fraction bar. Essentially, a fraction represents a part of a whole, where the numerator indicates the number of parts being considered, while the denominator signifies the total number of equal parts that make up the whole.
A fraction is commonly expressed in the form x/y, where ‘x’ represents the numerator and ‘y’ represents the denominator. Therefore, a fraction can be succinctly described as Numerator/Denominator. The number positioned above signifies the quantity of parts, while the number below the vinculum, i.e., the denominator, indicates the number of equal parts into which the item is divided.
Consider these examples:
- In the fraction 3/7, the numerator is 3.
- In the fraction 2/3, the numerator is 2, and the denominator is 3.
Let’s consider a real-world example: Imagine a pizza divided into 4 equal slices. How would you represent one slice of this pizza in relation to the whole? This can be expressed as the fraction 1/4, where:
- 1 → Numerator (representing the number of parts, i.e., one slice).
- 4 → Denominator (representing the total number of parts, i.e., four slices).
Are you still unsure about numerators? Do you want personalized guidance to help you master fractions and other mathematical concepts? Visit WHAT.EDU.VN to ask your questions and receive expert answers from our community of educators and math enthusiasts. We’re here to help you succeed
2. Numerator in Division
A fraction written as x/y is equivalent to x ÷ y, meaning x divided by y. In division, the numerator corresponds to the dividend, and the denominator corresponds to the divisor.
For instance, the fraction 1/2 is the same as 1 ÷ 2, which asks how many 2s are in 1. Here:
- 1 can be considered the dividend or the numerator.
- 2 can be considered the divisor or the denominator.
This understanding of numerators in division simplifies the process of solving mathematical problems, enhancing proficiency in arithmetic and algebraic operations.
3. Numerator in a Fraction Explained
Fractions can be categorized into various types based on their numerators and denominators, offering a more detailed understanding of their properties and applications.
3.1. Types of Fractions
- Proper Fractions: In proper fractions, the numerator is less than the denominator. These fractions represent a value less than 1. Examples include 1/2, 3/4, and 2/5.
- Improper Fractions: In improper fractions, the numerator is greater than or equal to the denominator. These fractions represent a value greater than or equal to 1. Examples include 5/3, 7/4, and 8/8.
- Mixed Fractions: Mixed fractions combine a whole number and a proper fraction. They represent values greater than 1. Examples include 1 1/2 (one and a half), 2 3/4 (two and three-quarters), and 3 1/4 (three and one-quarter).
- Unit Fractions: Unit fractions have a numerator of 1. They represent one part of a whole. Examples include 1/2, 1/3, 1/4, and 1/5.
- Like Fractions: Like fractions have the same denominator. This makes it easier to add or subtract them directly. Examples include 2/7, 3/7, and 5/7.
- Unlike Fractions: Unlike fractions have different denominators. To add or subtract them, you need to find a common denominator first. Examples include 1/3, 1/4, and 2/5.
- Equivalent Fractions: Equivalent fractions represent the same value, but have different numerators and denominators. They can be obtained by multiplying or dividing both the numerator and denominator by the same non-zero number. For example, 1/2, 2/4, and 3/6 are equivalent fractions.
- Complex Fractions: Complex fractions have a fraction in the numerator, denominator, or both. These can be simplified by multiplying the numerator by the reciprocal of the denominator. An example includes (1/2) / (3/4).
Understanding the nuances of each type of fraction enhances your ability to work with fractions in various mathematical contexts.
3.2. Tips for Remembering Numerator and Denominator
The simplest way to remember the difference between the numerator and the denominator is to understand their positions within the fraction.
Here’s a simple method:
- The numerator is always on top of the fraction bar.
- The denominator is always at the bottom of the fraction bar.
Identifying the numerator is straightforward. If you know where to look, you’ll easily find it. For example, in the fraction 1/2:
- The number above the fraction bar is the numerator, which in this case is 1.
- The number below the fraction bar is the denominator, which in this case is 2.
If you still find fractions challenging, don’t worry! WHAT.EDU.VN is here to help. You can ask any question and receive clear, step-by-step explanations from our knowledgeable community. Get the support you need to excel in math—visit WHAT.EDU.VN today
4. Numerator vs. Denominator: Key Differences
Both the numerator and denominator are essential components of a fraction, but they serve different roles. Here’s a detailed comparison presented in the table below:
| Feature | Numerator | Denominator |
|---|---|---|
| Position | Located at the top of the vinculum (fraction bar). | Located below the vinculum (fraction bar). |
| Representation | Represents the number of parts taken from the whole. | Represents the total number of equal parts into which the whole is divided. |
| Example (in the fraction 11/3) | 11 is the numerator. | 3 is the denominator. |
| Value | Indicates how many parts of the whole are being considered. | Indicates the total number of equal parts that make up the whole. |
| Impact on Fraction’s Value | Affects the value of the fraction directly; changing the numerator changes the quantity being represented. | Determines the size of each part; the larger the denominator, the smaller each part of the whole. |

4.1. Important Facts About the Numerator
Understanding the properties of the numerator can further clarify its role in fractions:
- Zero Numerator: When the numerator of a fraction is 0, the entire fraction equals 0. The value of the denominator does not matter. For example, 0/2 simplifies to 0.
- Equal Numerator and Denominator: If the numerator and the denominator are the same, the fraction simplifies to 1. For example, 4/4 = 1.
By grasping these fundamental differences and facts, you can better understand and manipulate fractions in various mathematical scenarios.
5. Numerator Examples
Let’s explore some practical examples to solidify your understanding of numerators:
Example 1: Class Composition
In a class of 28 students, 12 are girls. Determine the numerator of the fraction representing the boys in the class.
Solution:
The numerator represents the part, and the denominator represents the whole.
- Total number of students = 28
- Number of girls = 12
- Number of boys = 28 – 12 = 16
The fraction of boys in the class is the number of boys divided by the total number of students, which is 16/28. This fraction can be simplified to 4/7.
Therefore, the numerator of the fraction representing the boys in the class is 4.
Example 2: Rubik’s Cube
A Rubik’s Cube has 9 red-colored squares out of a total of 54 squares. Find the numerator of the fraction representing the red-colored squares.
Solution:
- Total number of squares = 54 (This is our denominator)
- Number of red squares = 9 (This is our numerator)
The fraction representing the red squares is 9/54, which simplifies to 1/6.
Therefore, the numerator of the fraction of red squares is 1.
Example 3: Sum of Numerator and Denominator
Find the sum of the numerator of the first fraction and the denominator of the second fraction: 1/4 and 4/5.
Solution:
- The numerator of the first fraction 1/4 is 1.
- The denominator of the second fraction 4/5 is 5.
The sum is 1 + 5 = 6.
Therefore, the sum is 6.
6. Practical Exercises on Numerators
To reinforce your understanding of numerators, try these practice questions:
Question 1:
In a fruit basket, there are 5 apples and 7 oranges. What is the numerator of the fraction representing the proportion of apples in the basket?
Answer:
Apples = 5
Oranges = 7
Total fruits = 5 + 7 = 12
Fraction of apples = 5/12
The numerator of the fraction representing the apples is 5.
Question 2:
A student scored 18 out of 25 questions correctly on a test. What is the numerator of the fraction representing the proportion of correctly answered questions?
Answer:
Correct answers = 18
Total questions = 25
Fraction of correct answers = 18/25
The numerator of the fraction representing the correctly answered questions is 18.
If you’re seeking more practice problems or need help understanding these solutions, remember that WHAT.EDU.VN offers personalized assistance. Our experts are available to answer your questions and provide detailed explanations. Don’t hesitate to reach out for help—visit WHAT.EDU.VN today!
7. FAQs on Numerator
7.1. What is the Meaning of Numerator?
In mathematics, a fraction has two parts: a numerator and a denominator. The numerator is the number located above the fraction bar or vinculum. For example, in the fraction 2/3, the numerator is 2.
7.2. What is Numerator and Denominator?
In a fraction of the form x/y, the number x above the line is the numerator, and the number y below the line is the denominator. The numerator represents the parts taken, while the denominator represents the total number of equal parts of the whole.
7.3. What is the Difference Between Numerator and Denominator?
The numerator is the number above the fraction bar, while the denominator is the number below the fraction bar. A fraction with 0 as the numerator is equal to 0, whereas a fraction with 0 as the denominator is undefined. In the fraction 5/3, 5 is the numerator, and 3 is the denominator.
7.4. What is a Common Numerator?
A common numerator refers to the least common multiple (LCM) of the numerators of two or more fractions. For example, in the expression 2/3 + 1/6, the numerators are 2 and 1. The LCM of 2 and 1 is 2. Thus, 2 is the common numerator. 2/3 remains as it is, and 1/6 can be written as (1 × 2)/(6 × 2) = 2/12.
7.5. How to Remember Numerator and Denominator?
Remembering the positions of the numerator and denominator in fractions makes it easier to differentiate between them. The numerator is always above the fraction bar, while the denominator is always below the bar.
7.6. How to Rationalize the Numerator?
Rationalizing the numerator involves converting the numerator from an irrational number to a rational number. This is achieved by multiplying both the numerator and the denominator by a number or an expression. For example, to rationalize the numerator in the number √3/2, multiply both the numerator and the denominator by √3. This yields (√3 ×√3)/(2 × √3) = 3/2√3.
7.7. Can the Numerator be Equal to 0?
Yes, the numerator of a fraction can be 0. A fraction of the form 0/a is always simplified to 0.
7.8. How to Find the Numerator and Denominator of a Fraction?
Identifying the numerator and the denominator of a fraction is straightforward. A fraction consists of two numbers. The number above the line is the numerator, and the number below the line is the denominator. In 4/5, the number 4 is the numerator, and the number 5 is the denominator.
Are you looking for more detailed explanations or need help with other mathematical concepts? WHAT.EDU.VN is here to assist you! Our platform provides quick, free answers to all your questions. Join our community today and get the support you need to succeed. Visit WHAT.EDU.VN now!
We understand that grasping mathematical concepts can sometimes be challenging, but remember, you’re not alone. At WHAT.EDU.VN, we’re dedicated to providing you with the resources and support you need to succeed. Whether you’re struggling with fractions, algebra, calculus, or any other math topic, our team of experts is here to help.
8. Need More Help? Ask WHAT.EDU.VN
Still have questions? Don’t hesitate to reach out. At WHAT.EDU.VN, we provide a free platform where you can ask any question and receive quick, accurate answers from our community of experts. We understand the challenges students face and are committed to making learning accessible and easy.
Why choose WHAT.EDU.VN?
- Free access: Ask unlimited questions without any cost.
- Fast responses: Get answers quickly from knowledgeable experts.
- Comprehensive support: Receive help with any subject or topic.
- Community-driven: Connect with other learners and experts.
- Easy to use: Our platform is designed to be simple and intuitive, so you can easily find the help you need.
How to get started:
- Visit our website: WHAT.EDU.VN
- Create a free account.
- Ask your question and provide any relevant details.
- Receive answers from our community of experts.
We’re here to help you succeed!
At WHAT.EDU.VN, our goal is to empower learners by providing the tools and resources they need to excel academically. We believe that everyone deserves access to quality education, and we’re committed to making that a reality.
Contact us:
- Address: 888 Question City Plaza, Seattle, WA 98101, United States
- WhatsApp: +1 (206) 555-7890
- Website: WHAT.EDU.VN
Don’t let your questions go unanswered. Join what.edu.vn today and get the help you need to achieve your academic goals!