A pentagon is a fundamental geometric shape characterized by five sides and five angles. The term “pentagon” originates from the Greek words “penta,” meaning five, and “gon,” meaning angle. As a polygon, the pentagon is a closed, two-dimensional figure formed by straight line segments. The sum of the interior angles in any pentagon is always 540 degrees.
Table of Contents:
- Pentagon Definition
- Types of Pentagons
- Properties of Pentagons
- Area of a Pentagon: Formulas
- Perimeter of a Pentagon: Formula
- Solved Problem: Area and Perimeter
- Special Types of Pentagons
- Line of Symmetry in a Pentagon
- Frequently Asked Questions (FAQs)
Pentagon Definition
A pentagon is defined as a polygon possessing five sides and five angles. Each side connects end-to-end, creating a closed figure. Therefore:
Number of Sides in a Pentagon = 5
Types of Pentagons
Like other polygons, pentagons come in various forms, categorized by their sides, angles, and vertices. The primary classifications are:
- Regular and Irregular Pentagons
- Convex and Concave Pentagons
Regular vs. Irregular Pentagons
A regular pentagon features five sides of equal length and five equal angles. In contrast, an irregular pentagon does not have equal side lengths or equal angle measures.
Regular Pentagon: A regular pentagon has five congruent sides.
We can divide a regular pentagon into five congruent isosceles triangles, radiating from the center. This property is helpful in calculating its area.
Convex vs. Concave Pentagons
A convex pentagon has all its vertices pointing outwards. Conversely, a concave pentagon has at least one vertex pointing inwards, making one of its interior angles greater than 180 degrees.
Properties of Pentagons
Key properties of pentagons include:
- The sum of the interior angles of a pentagon is 540°.
- A regular pentagon has equal sides and equal angles; otherwise, it is irregular.
- Each interior angle of a regular pentagon measures 108°, and each exterior angle measures 72°.
- An equilateral pentagon has five equal sides.
Area of a Pentagon: Formulas
The area of a pentagon can be calculated using different formulas depending on the available information:
-
Using Side Length and Apothem:
Area = (5/2) * Side Length * Apothem -
Using Only Side Length (s):
Area = (5 * s^2) / (4 * tan(36°)) -
Using Only Radius (r):
Area = (5/2) * r^2 * sin(72°)
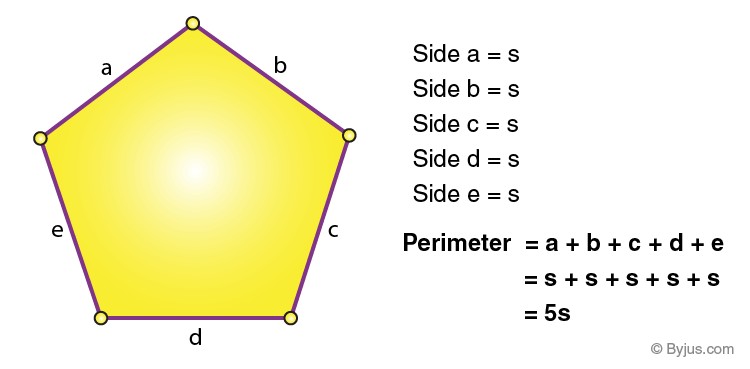
Perimeter of a Pentagon: Formula
The perimeter of a pentagon, especially a regular pentagon, is straightforward to calculate. Since all sides (‘a’) of a regular pentagon are equal, the perimeter is:
*Perimeter = 5 a**
Solved Problem: Area and Perimeter
Question: Calculate the area and perimeter of a regular pentagon with a side length of 5 cm and an apothem length of 6 cm.
Solution:
Given:
Side Length (a) = 5 cm
Apothem Length = 6 cm
Using the formulas:
Area = (5/2) * Side Length * Apothem = (5/2) * 5 cm * 6 cm = 75 cm²
Perimeter = 5 * a = 5 * 5 cm = 25 cm
Therefore, the area of the pentagon is 75 cm², and the perimeter is 25 cm.
Special Types of Pentagons
Equilateral Pentagons
An equilateral pentagon has five sides of equal length. However, its angles can vary, resulting in a family of pentagons rather than a single, unique shape like the regular pentagon.
Cyclic Pentagons
A cyclic pentagon is a pentagon whose vertices all lie on the circumference of a circle. A regular pentagon is a prime example of a cyclic pentagon.
Line of Symmetry in a Pentagon
A line of symmetry divides a shape into two identical halves. A regular pentagon has five lines of symmetry, each running from a vertex to the midpoint of the opposite side.
Frequently Asked Questions (FAQs)
Q1: How many sides does a pentagon have?
A: A pentagon has five sides and five angles.
Q2: What are the types of pentagons?
A: Types include simple, complex, regular, irregular, concave, convex, equilateral, and cyclic pentagons.
Q3: What is an irregular pentagon shape?
A: An irregular pentagon has unequal side lengths and angle measures.
Q4: What is a 12-sided shape called?
A: A 12-sided shape is called a Dodecagon.