Prime numbers are fundamental building blocks in the world of mathematics. Understanding What Is A Prime is essential for grasping more complex concepts in number theory, cryptography, and computer science. This guide provides a comprehensive overview of prime numbers, their properties, and how to identify them.
Defining Prime Numbers
A prime number is a whole number greater than 1 that has only two distinct positive divisors: 1 and itself. In simpler terms, a prime number cannot be evenly divided by any other number except 1 and the number itself.
For example, the number 7 is a prime number because its only factors are 1 and 7. Conversely, the number 8 is not a prime number because it has factors of 1, 2, 4, and 8. Numbers with more than two factors are called composite numbers.
Prime Number Definition Explained
To further clarify the definition, consider these key points:
- Greater than 1: The number 1 is not considered a prime number. It only has one factor (itself).
- Whole Number: Prime numbers are always whole numbers (integers). Fractions or decimals cannot be prime.
- Two Distinct Factors: The number must have exactly two different factors. A number with only one factor (like 1) or more than two factors (like 4) doesn’t qualify as prime.
List of Prime Numbers
Identifying prime numbers can be tricky, especially for larger numbers. Here’s a list of the first few prime numbers:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97…
Prime Numbers from 1 to 100
Here’s a breakdown of prime numbers within the range of 1 to 100:
| Range | Prime Numbers |
|---|---|
| 1 – 10 | 2, 3, 5, 7 |
| 11 – 20 | 11, 13, 17, 19 |
| 21 – 30 | 23, 29 |
| 31 – 40 | 31, 37 |
| 41 – 50 | 41, 43, 47 |
| 51 – 60 | 53, 59 |
| 61 – 70 | 61, 67 |
| 71 – 80 | 71, 73, 79 |
| 81 – 90 | 83, 89 |
| 91 – 100 | 97 |
Properties of Prime Numbers
Prime numbers possess several interesting properties:
- Divisibility: Prime numbers are only divisible by 1 and themselves.
- Uniqueness: Each composite number can be expressed as a unique product of prime numbers (the Fundamental Theorem of Arithmetic).
- Infinitude: There are infinitely many prime numbers. This was proven by Euclid over 2000 years ago.
- Even Prime: The number 2 is the only even prime number. All other even numbers are divisible by 2 and therefore have more than two factors.
- Co-prime: Any two prime numbers are always co-prime (their greatest common divisor is 1).
Prime Numbers vs. Composite Numbers
The key difference between prime and composite numbers lies in their number of factors:
- Prime Numbers: Have exactly two factors (1 and themselves).
- Composite Numbers: Have more than two factors.
For example:
- Prime: 11 (factors: 1, 11)
- Composite: 12 (factors: 1, 2, 3, 4, 6, 12)
Prime Numbers and Co-prime Numbers
While all prime numbers are co-prime with each other, co-prime numbers are not necessarily prime. Co-prime numbers (also known as relatively prime numbers) are two numbers whose greatest common factor (GCF) is 1. For example, 8 and 9 are co-prime because their only common factor is 1, even though both numbers are composite.
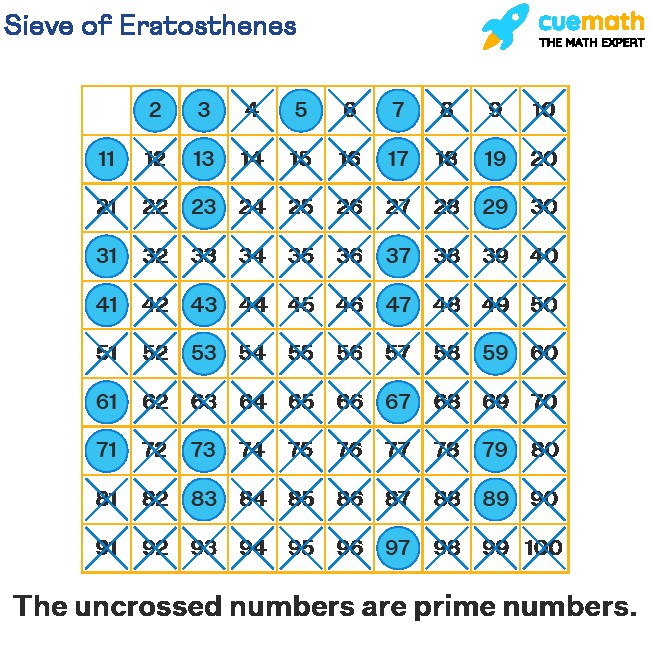Prime Numbers using the Sieve of Eratosthenes
Finding Prime Numbers: The Sieve of Eratosthenes
One of the oldest and most intuitive methods for finding prime numbers is the Sieve of Eratosthenes. This algorithm efficiently identifies all prime numbers up to a specified limit. Here’s how it works:
- Create a List: Write down all the whole numbers from 2 to the desired limit.
- Start with 2: Circle 2 as the first prime number.
- Eliminate Multiples of 2: Cross out all multiples of 2 (4, 6, 8, etc.) in the list.
- Next Uncrossed Number: Find the next uncrossed number in the list (which is 3). Circle it as the next prime number.
- Eliminate Multiples of 3: Cross out all multiples of 3 (6, 9, 12, etc.). Note that some numbers may already be crossed out.
- Repeat: Continue this process, finding the next uncrossed number, circling it as a prime, and eliminating its multiples, until you reach the square root of the limit.
- Remaining Numbers: All the circled numbers and the remaining uncrossed numbers in the list are prime numbers.
Special Types of Prime Numbers
Beyond the basic definition, there are several special types of prime numbers:
- Twin Primes: Pairs of prime numbers that differ by 2 (e.g., 3 and 5, 17 and 19).
- Mersenne Primes: Prime numbers of the form 2^p – 1, where p is also a prime number (e.g., 31 = 2^5 – 1).
- Fermat Primes: Prime numbers of the form 2^(2^n) + 1, where n is a non-negative integer (e.g., 5 = 2^(2^0) + 1).
Why are Prime Numbers Important?
Prime numbers are crucial in various fields, including:
- Cryptography: Prime numbers are the backbone of modern encryption algorithms like RSA, which secure online transactions and communications.
- Computer Science: Prime numbers are used in hashing algorithms, random number generation, and data compression.
- Number Theory: Prime numbers are central to number theory, a branch of mathematics that explores the properties and relationships of numbers.
Examples of Prime Number Problems
Let’s look at some examples to solidify our understanding of prime numbers:
Example 1: Is 37 a prime number?
- Check if 37 is divisible by any number between 2 and its square root (approximately 6).
- 37 is not divisible by 2, 3, 4, 5, or 6.
- Therefore, 37 is a prime number.
Example 2: Is 51 a prime number?
- Check if 51 is divisible by any number between 2 and its square root (approximately 7).
- 51 is divisible by 3 (51 / 3 = 17).
- Therefore, 51 is not a prime number; it’s a composite number.
The Significance of Prime Numbers
Prime numbers are more than just mathematical curiosities; they are essential components of many technologies and concepts that shape our modern world. Understanding what is a prime empowers you to appreciate the underlying structure and security of digital systems.
FAQs About Prime Numbers
What are prime numbers in math?
Prime numbers are whole numbers greater than 1 that have only two factors: 1 and themselves.
What are the examples of prime numbers?
Examples of prime numbers include 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29.
How to find prime numbers?
One method is to check if a number is divisible by any number other than 1 and itself. The Sieve of Eratosthenes is another efficient method for finding prime numbers up to a certain limit.
Why is 2 a prime number?
2 is a prime number because it has only two factors: 1 and 2. It’s also the only even prime number.
What are all the prime numbers from 1 to 100?
The prime numbers from 1 to 100 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97.
Which is the smallest prime number?
The smallest prime number is 2.
What is the difference between a prime and a co-prime number?
A prime number has only two factors (1 and itself). Co-prime numbers are two numbers whose greatest common factor (GCF) is 1, but they don’t necessarily have to be prime themselves.
Can prime numbers be negative?
No, prime numbers are always positive whole numbers greater than 1.
What are twin prime numbers?
Twin prime numbers are pairs of prime numbers that differ by 2 (e.g., 3 and 5, 17 and 19).
Which of the prime numbers are even numbers?
Only the number 2 is an even prime number.
Which numbers are not prime numbers?
Numbers that are not prime numbers are called composite numbers. They have more than two factors.
Are prime numbers odd?
Most prime numbers are odd, but the number 2 is an exception, as it is the only even prime number.
Which is the first prime number?
The first prime number is 2.
What are the even prime numbers from 1 to 100?
There is only one even prime number from 1 to 100, which is 2.
What is the greatest prime number between 1 and 10?
The greatest prime number between 1 and 10 is 7.
By understanding what is a prime number and its properties, you’ve taken a significant step in your mathematical journey. Prime numbers are the foundation for many advanced concepts, and their importance in modern technology cannot be overstated.
