What Is A Prime Number Definition? Explained Simply

Prime numbers can seem mysterious, but understanding what defines them is surprisingly straightforward. At WHAT.EDU.VN, we break down complex topics into easy-to-understand explanations. Discover the prime number definition, explore examples, and learn why they’re so important in mathematics. Expand your understanding of number theory with our accessible resources.

1. Understanding the Prime Number Definition

A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, a prime number can only be divided evenly by 1 and the number itself. This definition excludes 1, as it only has one divisor.

Natural Number: A positive whole number (1, 2, 3, 4, etc.).
Divisor: A number that divides another number evenly, leaving no remainder.
Composite Number: A natural number greater than 1 that has more than two divisors.

For example, 7 is a prime number because its only divisors are 1 and 7. On the other hand, 8 is not a prime number because it is divisible by 1, 2, 4, and 8. Numbers divisible by more than just 1 and themselves are composite numbers.

2. Exploring the History of Prime Numbers

The study of prime numbers dates back to ancient civilizations, particularly the Greeks.

Euclid (c. 300 BC): Proved that there are infinitely many prime numbers.
Eratosthenes (c. 240 BC): Developed the Sieve of Eratosthenes, a method for finding prime numbers.

The Sieve of Eratosthenes involves listing all natural numbers up to a certain limit and then iteratively marking the multiples of each prime, starting with 2. The numbers that remain unmarked are the prime numbers.

The exploration of prime numbers has continued through the centuries, with mathematicians like Fermat, Mersenne, and Euler making significant contributions.

3. Key Properties of Prime Numbers

Prime numbers exhibit several unique properties that make them fundamental in number theory.

Divisibility: Prime numbers are only divisible by 1 and themselves.
Infinitude: There are infinitely many prime numbers, as proven by Euclid.
Unique Factorization: Every integer greater than 1 can be expressed uniquely as a product of prime numbers (Fundamental Theorem of Arithmetic).
Distribution: Prime numbers become less frequent as numbers get larger, though predicting their exact distribution remains a challenge.

The unique factorization property is especially significant, as it forms the basis for many cryptographic algorithms.

4. Identifying Prime Numbers: Methods and Techniques

Several methods can be used to determine whether a number is prime.

Trial Division: Divide the number by all primes less than or equal to its square root. If none of them divide evenly, the number is prime.
Sieve of Eratosthenes: Efficient for finding all primes up to a given limit.
Primality Tests: More advanced algorithms like the Miller-Rabin test and the AKS primality test are used for very large numbers.

Example: Is 37 a Prime Number?

Find the square root of 37, which is approximately 6.08.
Test divisibility by primes less than 6.08 (2, 3, 5).
37 is not divisible by 2, 3, or 5.
Therefore, 37 is a prime number.

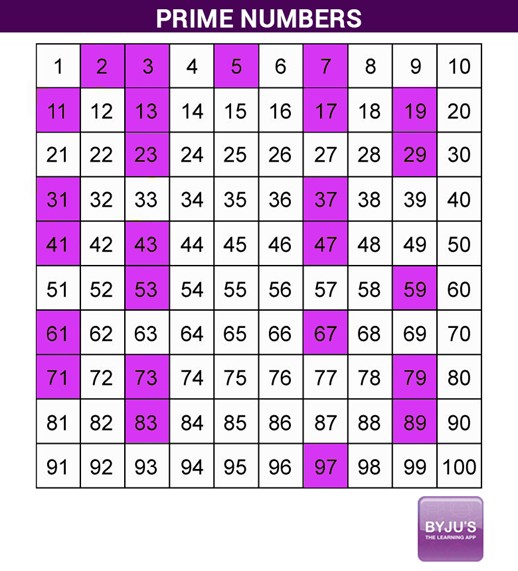
5. Common Examples of Prime Numbers

Understanding the prime number definition becomes easier when you consider a few examples. The smallest prime numbers are:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, …

Note: 2 is the only even prime number. All other prime numbers are odd.

6. Prime Numbers vs. Composite Numbers: Key Differences

The fundamental distinction between prime numbers and composite numbers lies in their divisors.

Feature	Prime Numbers	Composite Numbers
Definition	Divisible only by 1 and themselves	Divisible by 1, themselves, and at least one other number
Number of Factors	Exactly two	More than two
Examples	2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37	4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24

Understanding this distinction is crucial for grasping many concepts in number theory.

7. The Significance of Prime Numbers in Cryptography

Prime numbers play a critical role in modern cryptography, particularly in public-key cryptography systems like RSA (Rivest-Shamir-Adleman).

RSA Algorithm: Relies on the difficulty of factoring large numbers into their prime factors.
Key Generation: In RSA, two large prime numbers are chosen, and their product is used to create a public key.
Security: The security of RSA depends on the computational infeasibility of determining the original prime factors from the public key.

Without prime numbers, secure communication over the internet would be significantly more challenging. The prime number definition, therefore, extends far beyond theoretical mathematics.

8. Exploring Mersenne Primes and Perfect Numbers

Two special types of numbers are closely related to prime numbers: Mersenne primes and perfect numbers.

Mersenne Primes: Prime numbers of the form 2^n – 1, where n is also a prime number.
Perfect Numbers: Positive integers that are equal to the sum of their proper divisors (excluding the number itself).

Example:

2^2 – 1 = 3 (Mersenne Prime)
2^3 – 1 = 7 (Mersenne Prime)
2^5 – 1 = 31 (Mersenne Prime)

If 2^p – 1 is a Mersenne prime (where p is prime), then 2^(p-1) * (2^p – 1) is a perfect number.

Example:

For p = 2, 2^(2-1) (2^2 – 1) = 2 3 = 6 (Perfect Number: 1 + 2 + 3 = 6)
For p = 3, 2^(3-1) (2^3 – 1) = 4 7 = 28 (Perfect Number: 1 + 2 + 4 + 7 + 14 = 28)

9. Practical Applications of Prime Numbers

Beyond cryptography, prime numbers have various practical applications.

Hashing Algorithms: Used in computer science for data storage and retrieval.
Random Number Generators: Employed in simulations and statistical analysis.
Error Correction Codes: Utilized in data transmission to detect and correct errors.

10. Prime Numbers in Nature and Art

While prime numbers are primarily a mathematical concept, some intriguing connections can be found in nature and art.

Cicada Life Cycles: Some species of cicadas have life cycles that are prime numbers (e.g., 13 years, 17 years), possibly as an evolutionary strategy to avoid predators with cyclical life patterns.
Musical Composition: Some composers have explored prime numbers in structuring musical pieces, creating patterns and rhythms based on prime sequences.

11. Formulas and Theorems Related to Prime Numbers

Many formulas and theorems relate to prime numbers, providing insights into their distribution and properties.

Prime Number Theorem: Provides an estimate for the number of primes less than or equal to a given number.
Dirichlet’s Theorem on Arithmetic Progressions: States that if a and b are coprime integers, then the arithmetic progression a + nb (where n is a non-negative integer) contains infinitely many primes.
Goldbach’s Conjecture: Every even integer greater than 2 can be expressed as the sum of two primes (unproven).

12. The Challenge of Factoring Large Numbers

The difficulty of factoring large numbers into their prime factors is a cornerstone of modern cryptography. As numbers get larger, the computational effort required to factor them increases dramatically.

Computational Complexity: Factoring large numbers is believed to be a computationally hard problem, meaning that the time required to solve it grows exponentially with the size of the number.
Quantum Computing: The development of quantum computers poses a potential threat to current cryptographic systems, as they could potentially factor large numbers much more efficiently using algorithms like Shor’s algorithm.

13. Tips for Remembering Prime Numbers

Memorizing prime numbers can be helpful for various mathematical tasks. Here are some tips:

Start with the Basics: Memorize the first few prime numbers (2, 3, 5, 7, 11, 13, 17, 19, 23, 29).
Use Flashcards: Create flashcards with numbers and test yourself to identify prime numbers.
Look for Patterns: While there isn’t a simple pattern to prime numbers, recognizing that all primes greater than 2 are odd can help.
Practice Regularly: The more you work with prime numbers, the easier it will become to remember them.

14. Why Prime Numbers Matter in Computer Science

In computer science, prime numbers are essential for data security, algorithm design, and more.

Cryptography: Securing online transactions and communications.
Hashing: Creating efficient data structures.
Random Number Generation: Ensuring the randomness of simulations and algorithms.

15. Demystifying Prime Number Distribution

The distribution of prime numbers is an area of ongoing research in mathematics. While there is no simple formula for predicting the next prime number, several theorems and conjectures provide insights.

Prime Number Theorem: Approximates the number of primes less than or equal to a given number.
Riemann Hypothesis: A famous unsolved problem in mathematics that has implications for the distribution of prime numbers.

16. Advanced Concepts: Twin Primes and Prime Gaps

Twin primes and prime gaps are advanced concepts that illustrate the complexities of prime number distribution.

Twin Primes: Pairs of prime numbers that differ by 2 (e.g., 3 and 5, 5 and 7, 11 and 13).
Prime Gaps: The difference between consecutive prime numbers.

The twin prime conjecture, which states that there are infinitely many twin primes, remains unproven.

17. The Role of Prime Numbers in Data Compression

Data compression techniques can sometimes leverage prime numbers to optimize storage and transmission.

Run-Length Encoding (RLE): In specific scenarios, prime numbers can be used to represent repeated sequences of data efficiently.
Number Theory Transforms: Advanced compression algorithms may use number theory concepts related to prime numbers.

18. Exploring Prime Factorization Techniques

Prime factorization is the process of expressing a composite number as a product of prime numbers. Several techniques can be used:

Trial Division: Divide the number by primes starting with 2 until you are left with a prime number.
Factor Tree: Create a tree-like diagram to break down the number into its prime factors.
Pollard’s Rho Algorithm: An efficient algorithm for factoring large numbers.

Example: Prime Factorization of 84

84 ÷ 2 = 42
42 ÷ 2 = 21
21 ÷ 3 = 7
7 is a prime number

Therefore, the prime factorization of 84 is 2 × 2 × 3 × 7, or 2^2 × 3 × 7.

19. Prime Numbers and the Riemann Hypothesis

The Riemann hypothesis, proposed by Bernhard Riemann in 1859, is one of the most famous unsolved problems in mathematics. It has profound implications for the distribution of prime numbers.

Riemann Zeta Function: The hypothesis concerns the zeros of the Riemann zeta function.
Prime Distribution: If the Riemann hypothesis is true, it would provide a much more precise understanding of how prime numbers are distributed.

20. Fun Facts About Prime Numbers

To make prime numbers more engaging, here are some fun facts:

2 is the only even prime number.
The largest known prime number has over 24 million digits.
Prime numbers are used in generating secure passwords.
Some species of cicadas have prime-numbered life cycles.

21. Using Prime Numbers in Hashing Algorithms

Hashing algorithms rely on prime numbers to distribute data evenly across a hash table, minimizing collisions and ensuring efficient data retrieval.

Hash Function: A function that maps data to a fixed-size value.
Collision: When two different data items map to the same hash value.
Prime Numbers: Used to determine the size of the hash table and in the hash function itself.

22. Prime Numbers in Modular Arithmetic

Modular arithmetic, also known as clock arithmetic, involves performing arithmetic operations within a specific modulus. Prime numbers play a key role in modular arithmetic.

Modulus: The number that determines the range of values.
Prime Modulus: Using a prime number as the modulus has special properties that are useful in cryptography and computer science.

23. How Prime Numbers Relate to Error Correction

Error correction codes use prime numbers to detect and correct errors in data transmission and storage.

Redundancy: Error correction codes add extra information to the data to detect and correct errors.
Prime Numbers: Used in the design of error correction codes to ensure efficient error detection and correction.

24. The Ongoing Search for New Prime Numbers

The search for new prime numbers is an ongoing effort, with mathematicians and computer scientists continually pushing the boundaries.

Great Internet Mersenne Prime Search (GIMPS): A collaborative project that uses distributed computing to search for Mersenne primes.
Computational Power: Finding larger and larger prime numbers requires significant computational resources.

25. Prime Numbers and Random Number Generation

Prime numbers are used in the generation of random numbers, which are essential for simulations, cryptography, and other applications.

Linear Congruential Generators (LCGs): A common type of random number generator that uses prime numbers in its formula.
Cryptographic Security: Using prime numbers in random number generators can improve the security of cryptographic systems.

26. What is the Largest Known Prime Number?

As of the latest updates, the largest known prime number is 2^82,589,933 – 1. This number has a staggering 24,862,048 digits and was discovered by the Great Internet Mersenne Prime Search (GIMPS). The search for larger prime numbers continues, driven by both theoretical interest and practical applications.

27. How to Test if a Large Number is Prime?

Testing whether a large number is prime involves advanced algorithms, given the inefficiency of simple trial division.

Miller-Rabin Primality Test: A probabilistic algorithm that provides a high degree of certainty.
AKS Primality Test: The first deterministic polynomial-time primality test, but less practical for very large numbers.

28. Prime Numbers and the Distribution of Zeros

The distribution of zeros of the Riemann zeta function is intimately connected with the distribution of prime numbers. This relationship is a central focus of the Riemann hypothesis.

Complex Analysis: Understanding the zeros of the Riemann zeta function requires advanced techniques from complex analysis.
Number Theory: The relationship between zeros and prime numbers has profound implications for number theory.

29. Exploring Special Types of Prime Numbers

Besides Mersenne primes, there are other special types of prime numbers that mathematicians find intriguing.

Sophie Germain Primes: A prime p such that 2p + 1 is also prime.
Wieferich Primes: A prime p such that 2^(p-1) ≡ 1 (mod p^2).

30. The Connection Between Prime Numbers and Continued Fractions

Continued fractions provide a way to represent real numbers as a sequence of integers. Prime numbers are related to continued fractions in various ways.

Representation of Irrational Numbers: Continued fractions can be used to represent irrational numbers, such as the square root of a prime number.
Approximation of Real Numbers: Continued fractions can provide good approximations of real numbers, which is useful in various applications.

31. Understanding the Prime Counting Function

The prime counting function, denoted by π(x), gives the number of prime numbers less than or equal to x. Understanding the behavior of this function is a key goal in number theory.

Asymptotic Behavior: The prime number theorem provides an asymptotic estimate for π(x).
Riemann Hypothesis: The Riemann hypothesis would provide a more precise estimate for π(x).

32. Prime Numbers in Quantum Cryptography

Quantum cryptography leverages the principles of quantum mechanics to provide secure communication. Prime numbers play a role in some quantum cryptographic protocols.

Quantum Key Distribution (QKD): Protocols that use quantum mechanics to establish a secret key.
Security: The security of QKD protocols relies on the laws of physics rather than computational assumptions.

33. How Prime Numbers Are Used in Checksums

Checksums are used to verify the integrity of data by calculating a value based on the data. Prime numbers are used in some checksum algorithms.

Data Integrity: Checksums help detect errors that may occur during data transmission or storage.
Prime Numbers: Used in the design of checksum algorithms to provide good error detection capabilities.

34. The Sieve of Atkin and Its Efficiency

The Sieve of Atkin is an efficient algorithm for finding all prime numbers up to a specified integer. It improves upon the Sieve of Eratosthenes.

Optimization: The Sieve of Atkin uses various optimizations to reduce the number of computations required.
Performance: For large ranges of numbers, the Sieve of Atkin can be significantly faster than the Sieve of Eratosthenes.

35. Prime Numbers and Elliptic Curve Cryptography

Elliptic curve cryptography (ECC) is a type of public-key cryptography that is based on the algebraic structure of elliptic curves over finite fields. Prime numbers are used in the construction of these finite fields.

Security: ECC offers strong security with relatively small key sizes, making it suitable for resource-constrained environments.
Applications: ECC is used in various applications, including secure web browsing and digital signatures.

36. Using Prime Numbers in Digital Signatures

Digital signatures are used to verify the authenticity and integrity of digital documents. Prime numbers are used in various digital signature algorithms.

Authentication: Digital signatures provide a way to verify the identity of the signer.
Non-Repudiation: Digital signatures prevent the signer from denying having signed the document.

37. How Prime Numbers Are Used in RAID Systems

Redundant Array of Independent Disks (RAID) systems use multiple hard drives to provide data redundancy and improve performance. Prime numbers are used in some RAID configurations.

Data Redundancy: RAID systems ensure that data is not lost if a hard drive fails.
Performance: RAID systems can improve the speed of data access.

38. Prime Numbers in Network Protocols

Network protocols use prime numbers in various ways to ensure secure and reliable communication.

Secure Shell (SSH): Uses prime numbers in key exchange algorithms.
Transport Layer Security (TLS): Uses prime numbers in cryptographic operations.

39. Prime Numbers and the Law of Quadratic Reciprocity

The law of quadratic reciprocity is a theorem in number theory that relates the solvability of quadratic equations modulo different prime numbers.

Quadratic Residues: The law of quadratic reciprocity concerns the conditions under which an integer is a quadratic residue modulo a prime number.
Number Theory: This law is a fundamental result in number theory with many applications.

40. Prime Numbers in Pseudorandom Number Sequences

Pseudorandom number sequences are used in various applications, including simulations and cryptography. Prime numbers are used in the construction of some pseudorandom number generators.

Period Length: Prime numbers can help increase the period length of pseudorandom number sequences.
Statistical Properties: Using prime numbers can improve the statistical properties of pseudorandom number sequences.

41. Prime Numbers and the Goldbach Conjecture

The Goldbach conjecture, one of the oldest and best-known unsolved problems in number theory, states that every even integer greater than 2 can be expressed as the sum of two prime numbers.

Unproven Conjecture: Despite extensive research, the Goldbach conjecture remains unproven.
Computational Verification: The conjecture has been verified computationally for very large numbers.

42. Exploring Prime Number Spirals

Prime number spirals, such as the Ulam spiral, are graphical representations that reveal patterns in the distribution of prime numbers.

Ulam Spiral: A spiral arrangement of numbers in which prime numbers tend to cluster along certain diagonal lines.
Visual Representation: Prime number spirals provide a visual way to explore the distribution of prime numbers.

43. Prime Numbers and Perfect Hash Functions

Perfect hash functions map a set of keys to a set of hash values without any collisions. Prime numbers are used in the construction of some perfect hash functions.

Collision-Free Mapping: Perfect hash functions guarantee that each key maps to a unique hash value.
Efficient Data Retrieval: Perfect hash functions enable very fast data retrieval.

44. Prime Numbers in the Design of Bloom Filters

Bloom filters are probabilistic data structures that are used to test whether an element is a member of a set. Prime numbers are used in the design of Bloom filters.

Space Efficiency: Bloom filters are very space-efficient.
False Positives: Bloom filters can produce false positives, but the probability of a false positive can be controlled.

45. Prime Numbers and Fibonacci Numbers

Fibonacci numbers are a sequence of numbers in which each number is the sum of the two preceding ones (e.g., 1, 1, 2, 3, 5, 8, 13, …). Prime numbers are related to Fibonacci numbers in various ways.

Fibonacci Primes: Fibonacci numbers that are also prime numbers.
Divisibility Properties: Prime numbers can have special divisibility properties with respect to Fibonacci numbers.

Understanding the prime number definition opens up a world of mathematical and computational possibilities. At WHAT.EDU.VN, we’re here to help you explore these fascinating concepts and answer any questions you may have.

Still have questions about prime numbers or other math topics? Don’t hesitate to ask! Visit WHAT.EDU.VN today to post your questions and receive free, expert answers from our community. Our address is 888 Question City Plaza, Seattle, WA 98101, United States, and you can reach us on WhatsApp at +1 (206) 555-7890. Let what.edu.vn be your go-to resource for all your learning needs!