What Is A Prism? Definition, Types, and Applications

What Is A Prism? Let WHAT.EDU.VN illuminate this fascinating geometric shape. This comprehensive guide explores the prism definition, its various types, practical applications, and formulas. Discover the science and math behind prisms and unlock their secrets. Dive in and ask your questions on WHAT.EDU.VN for free answers and expert insights, enriching your understanding of these polyhedrons, geometric solids, and optical elements.

1. Understanding the Basic Prism Definition

A prism is a three-dimensional geometric shape characterized by two parallel, identical bases connected by flat faces. These connecting faces are parallelograms, making the prism a polyhedron with uniform cross-sections throughout its length. Prisms are commonly recognized in optics, mathematics, and architecture due to their unique properties and shapes.

• The bases determine the prism’s name (e.g., triangular prism, rectangular prism).
• The lateral faces are always parallelograms.
• Prisms have consistent cross-sectional area along their height.

2. Key Elements and Properties of a Prism

To fully grasp what is a prism, it’s essential to understand its components and characteristics. These elements define its structure and influence its properties.

2.1. Faces, Edges, and Vertices Explained

• Faces: These are the flat surfaces that enclose the prism. A prism has two bases and several lateral faces.
• Edges: An edge is a line segment where two faces meet.
• Vertices: These are the corners where edges intersect.

2.2. Characteristics of a Prism

Characteristic	Description
Base Shape	Determines the name of the prism (e.g., triangle, square, pentagon).
Lateral Faces	Always parallelograms; can be rectangles or squares in right prisms.
Parallel Bases	The two bases are identical and parallel to each other.
Uniform Cross-Section	The shape and area of cross-sections parallel to the bases are consistent along the prism’s height.
Three-Dimensional Shape	Prisms occupy space in three dimensions, having length, width, and height.

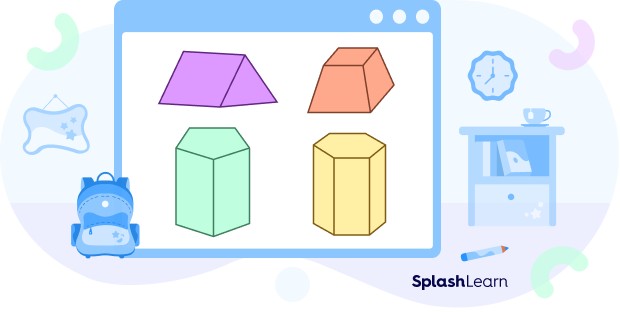
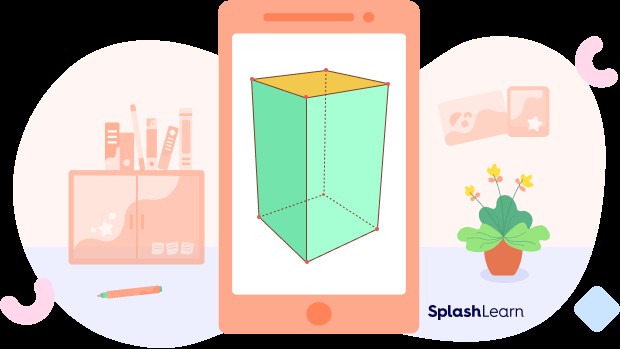
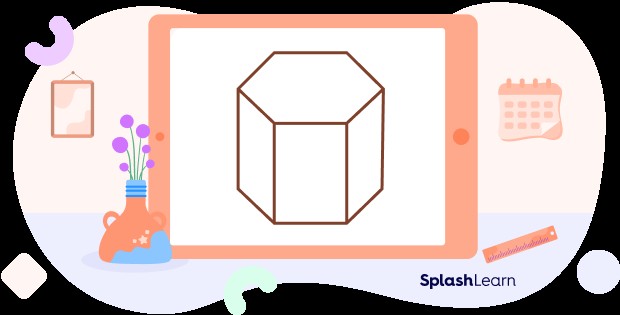
3. Exploring Different Types of Prisms

Prisms come in various forms, each with distinct attributes. Understanding these types helps to appreciate the diversity and versatility of prisms.

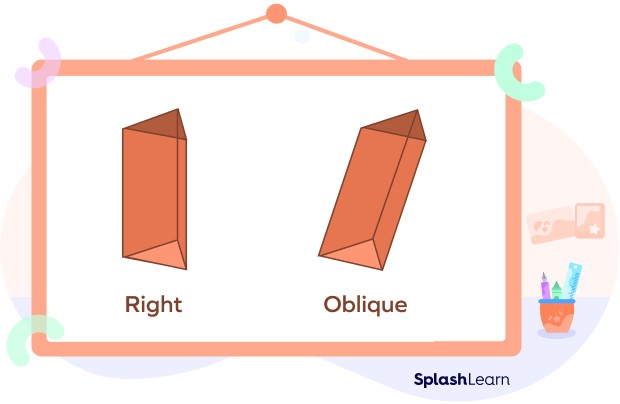
3.1. Right Prism vs. Oblique Prism

• Right Prism: In a right prism, the lateral faces are perpendicular to the bases. This means the connecting faces stand upright, forming a 90-degree angle with the bases.

• Oblique Prism: An oblique prism is one where the lateral faces are not perpendicular to the bases. It leans to one side, resulting in non-rectangular lateral faces.

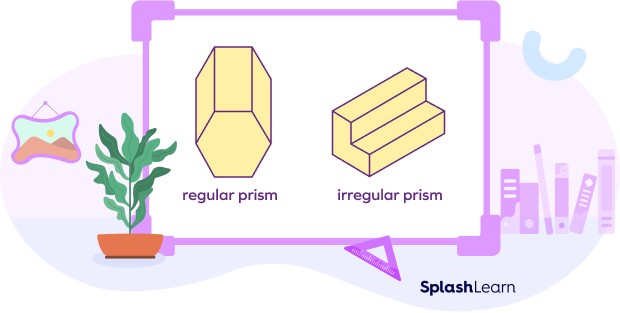
3.2. Regular Prism vs. Irregular Prism

• Regular Prism: A regular prism has bases that are regular polygons. A regular polygon has equal sides and equal angles.
• Irregular Prism: In contrast, an irregular prism features bases that are irregular polygons, where the sides and angles are not equal.

3.3. Classification by Base Shape (Triangular, Rectangular, Pentagonal, Hexagonal)

Prisms are often categorized by the shape of their bases. This classification helps to quickly identify their geometric properties and applications.

• Triangular Prism: Has triangular bases and three rectangular lateral faces.

• Rectangular Prism: Features rectangular bases and four rectangular lateral faces. A cube is a special case of a rectangular prism where all faces are squares.

• Pentagonal Prism: Comes with pentagonal bases and five rectangular lateral faces.

• Hexagonal Prism: Owns hexagonal bases and six rectangular lateral faces.

4. Understanding Prism Geometry: Surface Area and Volume

Delving into the geometry of prisms involves understanding how to calculate their surface area and volume. These calculations are critical in various fields, including engineering and architecture.

4.1. Calculating Surface Area: Formula and Examples

The surface area of a prism is the sum of the areas of all its faces.

Formula for Surface Area

• Surface Area = (2 × Base Area) + (Base Perimeter × Height)

Examples

Example 1: Find the surface area of a triangular prism with a base area of 30 cm², a base perimeter of 20 cm, and a height of 15 cm.

• Surface Area = (2 × 30) + (20 × 15) = 60 + 300 = 360 cm²

Example 2: Calculate the surface area of a rectangular prism with a base area of 50 cm², a base perimeter of 30 cm, and a height of 10 cm.

• Surface Area = (2 × 50) + (30 × 10) = 100 + 300 = 400 cm²

Example 3: Determine the surface area of a pentagonal prism with a base area of 75 cm², a base perimeter of 40 cm, and a height of 20 cm.

• Surface Area = (2 × 75) + (40 × 20) = 150 + 800 = 950 cm²

4.2. Calculating Volume: Formula and Examples

The volume of a prism is the amount of space it occupies.

Formula for Volume

• Volume = Base Area × Height

Examples

Example 1: Calculate the volume of a triangular prism with a base area of 25 cm² and a height of 12 cm.

• Volume = 25 × 12 = 300 cm³

Example 2: Find the volume of a rectangular prism with a base area of 60 cm² and a height of 8 cm.

• Volume = 60 × 8 = 480 cm³

Example 3: Determine the volume of a pentagonal prism with a base area of 90 cm² and a height of 10 cm.

• Volume = 90 × 10 = 900 cm³

5. Real-World Applications of Prisms

Prisms are not just theoretical geometric shapes; they have numerous practical applications in various fields.

5.1. Optical Prisms in Science and Technology

Optical prisms are used to refract and disperse light. They are vital in:

• Spectroscopy: Separating light into its component colors for analysis.
• Binoculars and Telescopes: Correcting and enhancing images.
• Cameras: Directing light within the camera system.
• Laser Technology: Manipulating laser beams for various applications.

5.2. Prisms in Architecture and Engineering

Prisms are used in architecture and engineering for structural and aesthetic purposes:

• Structural Support: Prism-shaped beams provide robust support in buildings and bridges.
• Decorative Elements: Prisms add visual interest and unique design elements to structures.
• Skylights: Triangular prisms can be used to design skylights that maximize natural light.

5.3. Everyday Examples of Prisms

Prisms can be found in everyday objects:

• Tents: Many tents use triangular prism designs for stability and space.
• Chocolate Bars: Some chocolate bars are shaped like triangular prisms.
• Doorstops: Wedge-shaped doorstops are a form of triangular prism.

6. Common Questions About Prisms Answered

To further clarify the topic of prisms, let’s address some frequently asked questions.

6.1. How is a Prism Different from a Pyramid?

Feature	Prism	Pyramid
Bases	Two identical, parallel bases	One base
Lateral Faces	Parallelograms	Triangles
Cross-Section	Uniform throughout the length	Varies from base to apex
Key Difference	Two bases connected by lateral faces	Single base converging to an apex

6.2. Can We Regard a Cylinder as a Prism?

No, a cylinder cannot be regarded as a prism. A prism is a polyhedron with flat faces, while a cylinder has curved surfaces.

6.3. What is the Difference Between a Right Prism and an Oblique Prism?

In a right prism, the lateral faces are perpendicular to the bases. In an oblique prism, the lateral faces are not perpendicular to the bases, causing the prism to lean.

7. Formulas for Calculating Prism Properties

To sum up, here are the key formulas for calculating properties of prisms:

7.1. Surface Area Formulas

• General Formula: Surface Area = (2 × Base Area) + (Base Perimeter × Height)
• Triangular Prism: Surface Area = (b × h) + (3 × s × l), where b = base, h = height of triangle, s = side length, l = prism length
• Rectangular Prism: Surface Area = 2(lw + lh + wh), where l = length, w = width, h = height

7.2. Volume Formulas

• General Formula: Volume = Base Area × Height
• Triangular Prism: Volume = (1/2 × b × h) × l, where b = base, h = height of triangle, l = prism length
• Rectangular Prism: Volume = l × w × h, where l = length, w = width, h = height

8. Test Your Knowledge About Prisms

8.1. Interactive Quiz Questions

1. What is the surface area of a rectangular prism with length 5 cm, width 3 cm, and height 4 cm?
   • A) 47 cm²
   • B) 94 cm²
   • C) 60 cm²
   • D) 70 cm²
2. What is the volume of a triangular prism with a base area of 20 cm² and a height of 10 cm?
   • A) 100 cm³
   • B) 200 cm³
   • C) 300 cm³
   • D) 400 cm³
3. Which of the following is NOT a type of prism?
   • A) Triangular Prism
   • B) Square Prism
   • C) Cylinder
   • D) Pentagonal Prism

8.2. Answers and Explanations

1. B) 94 cm² Explanation: Surface Area = 2(lw + lh + wh) = 2((5×3) + (5×4) + (3×4)) = 2(15 + 20 + 12) = 2(47) = 94 cm²
2. B) 200 cm³ Explanation: Volume = Base Area × Height = 20 cm² × 10 cm = 200 cm³
3. C) Cylinder Explanation: A cylinder has a curved surface, while prisms have flat faces.

9. The Importance of Understanding Prisms

Understanding prisms is crucial for various reasons:

• Educational Value: Prisms are fundamental geometric shapes taught in schools.
• Practical Applications: They are used in optics, architecture, and engineering.
• Problem-Solving Skills: Studying prisms enhances spatial reasoning and problem-solving abilities.
• Technological Advancements: Prisms play a significant role in modern technologies.

10. Tips for Further Learning About Prisms

To deepen your understanding of prisms:

• Explore Online Resources: Utilize educational websites like WHAT.EDU.VN for comprehensive information.
• Practice Problems: Solve various problems to reinforce your understanding of surface area and volume calculations.
• Hands-On Activities: Use physical models to visualize different types of prisms.
• Consult Experts: Ask questions on platforms like WHAT.EDU.VN to get answers from knowledgeable individuals.

11. Advanced Concepts Related to Prisms

For those looking to delve deeper, here are some advanced concepts:

• Truncated Prisms: Prisms with non-parallel top and bottom faces.
• Prismatoids: Polyhedra with polygonal bases in parallel planes.
• Applications in Computer Graphics: Using prisms in 3D modeling and rendering.

12. The Role of Prisms in Optical Illusions

Prisms are often used to create optical illusions and visual effects. Their ability to refract light can be manipulated to produce surprising and engaging experiences.

12.1. Creating Visual Effects

• Light Bending: Prisms bend light, creating the illusion of displaced or distorted images.
• Color Separation: They split white light into a spectrum, producing rainbow-like effects.

12.2. Examples in Art and Entertainment

• Holograms: Prisms are used to create holographic images.
• Stage Lighting: They create dramatic lighting effects in theater productions.

13. How Prisms Contribute to Technological Advancements

Prisms are essential in several technological advancements, including:

13.1. Use in Spectrometers

Spectrometers use prisms to analyze the composition of light, helping scientists identify different elements and compounds.

13.2. Role in Fiber Optics

Prisms help in directing light within fiber optic cables, improving the efficiency of data transmission.

13.3. Applications in Medical Devices

Prisms are used in medical devices like endoscopes and microscopes, enhancing imaging capabilities.

14. Fun Facts About Prisms

• Rainbows: Natural prisms, like raindrops, create rainbows by dispersing sunlight.
• Historical Use: Ancient civilizations used prisms for decorative and scientific purposes.
• Modern Art: Artists use prisms to create unique visual effects in sculptures and installations.

15. Where to Find More Information About Prisms

• Educational Websites: WHAT.EDU.VN provides detailed explanations and resources.
• Textbooks: Geometry and physics textbooks offer comprehensive coverage.
• Scientific Journals: Research articles provide advanced insights into prism applications.

16. Encouraging Further Exploration of Prisms

Prisms are fascinating geometric shapes with numerous applications. By exploring their properties and uses, you can gain a deeper appreciation for mathematics, science, and technology.

16.1. Recommended Resources

• WHAT.EDU.VN: For quick answers and free expert insights.
• Khan Academy: Offers free math and science tutorials.
• Physics Classroom: Provides detailed explanations of optical phenomena.

16.2. Call to Action

Have more questions about prisms? Visit WHAT.EDU.VN today to ask your questions and get free answers from our community of experts. We are located at 888 Question City Plaza, Seattle, WA 98101, United States. You can also reach us via WhatsApp at +1 (206) 555-7890 or visit our website at what.edu.vn. Don’t hesitate to explore the world of prisms and unlock their secrets with us!