A quadratic equation is a polynomial equation of the second degree. It’s a fundamental concept in algebra with wide-ranging applications in various fields. This guide provides a comprehensive overview of quadratic equations, covering their definition, properties, methods of solving, and real-world applications.
Understanding Quadratic Equations
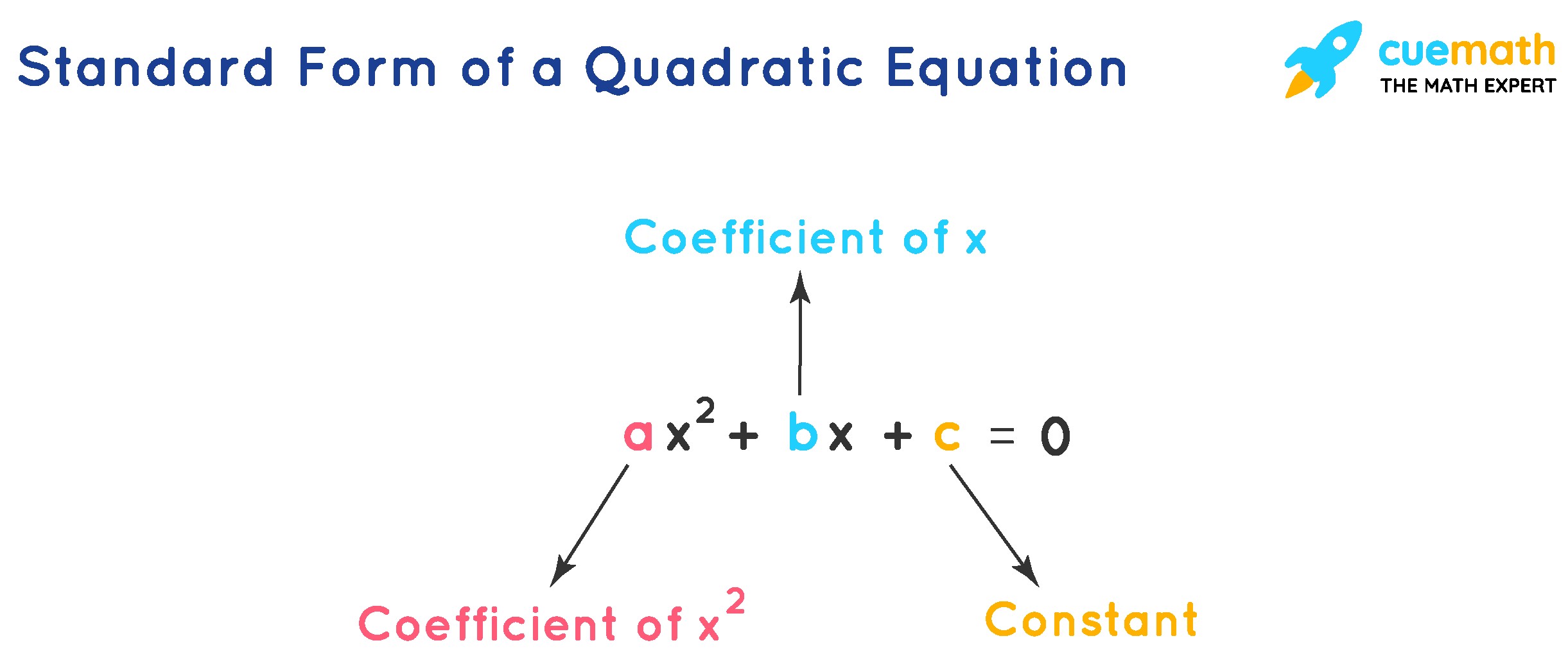
A quadratic equation is generally expressed in the standard form:
ax² + bx + c = 0
Where:
- x represents the variable or unknown.
- a, b, and c represent constants, where ‘a’ is not equal to zero (a ≠ 0). If a = 0, the equation becomes a linear equation.
- a is the quadratic coefficient.
- b is the linear coefficient.
- c is the constant term or the y-intercept
Roots of a Quadratic Equation
The “roots” of a quadratic equation are the values of ‘x’ that satisfy the equation, making the equation equal to zero. A quadratic equation has a maximum of two roots, which can be real or complex numbers. These roots are also known as solutions or zeros of the equation.
Methods for Solving Quadratic Equations
There are several methods to find the roots of a quadratic equation:
1. Factoring
Factoring involves expressing the quadratic equation as a product of two linear factors. For example:
x² + 5x + 6 = 0
Can be factored as:
(x + 2)(x + 3) = 0
Setting each factor to zero gives the roots:
x = -2 or x = -3
2. Quadratic Formula
The quadratic formula is a general method that can be used to solve any quadratic equation, regardless of whether it can be factored easily. The formula is:
x = [-b ± √(b² – 4ac)] / 2a
This formula provides two possible solutions for x, one using the plus sign and the other using the minus sign. It’s also known as the Sridharacharya formula.
Example:
For the equation x² – 3x – 4 = 0, where a = 1, b = -3, and c = -4:
x = [-(-3) ± √((-3)² – 4(1)(-4))] / 2(1)
x = [3 ± √(9 + 16)] / 2
x = [3 ± √25] / 2
x = [3 ± 5] / 2
Thus, x = 4 or x = -1
3. Completing the Square
Completing the square involves manipulating the quadratic equation to create a perfect square trinomial on one side of the equation.
Starting with ax² + bx + c = 0:
- Divide by ‘a’: x² + (b/a)x + c/a = 0
- Move the constant term to the right side: x² + (b/a)x = -c/a
- Add (b/2a)² to both sides: x² + (b/a)x + (b/2a)² = -c/a + (b/2a)²
- Factor the left side: (x + b/2a)² = (b² – 4ac) / 4a²
- Take the square root of both sides: x + b/2a = ±√(b² – 4ac) / 2a
- Solve for x: x = [-b ± √(b² – 4ac)] / 2a
4. Graphing
A quadratic equation can be represented graphically as a parabola. The points where the parabola intersects the x-axis represent the real roots of the equation.
The Discriminant
The discriminant (D) of a quadratic equation is the part of the quadratic formula under the square root:
D = b² – 4ac
The discriminant provides information about the nature of the roots:
- D > 0: The equation has two distinct real roots.
- D = 0: The equation has two equal real roots (a repeated root).
- D < 0: The equation has two complex roots.
Sum and Product of Roots
For a quadratic equation ax² + bx + c = 0, the sum and product of the roots (α and β) are given by:
- Sum of roots (α + β) = -b/a
- Product of roots (αβ) = c/a
If you know the roots of a quadratic equation, you can construct the equation as follows:
x² – (α + β)x + αβ = 0
Real-World Applications
Quadratic equations have numerous applications in various fields:
- Physics: Projectile motion, calculating trajectories.
- Engineering: Designing bridges, arches, and other structures.
- Astronomy: Calculating orbits of celestial bodies.
- Economics: Modeling supply and demand curves.
- Computer Graphics: Creating curves and surfaces.
Maximum and Minimum Values
The graph of a quadratic equation is a parabola. If ‘a’ > 0, the parabola opens upwards, and the vertex represents the minimum value of the function. If ‘a’ < 0, the parabola opens downwards, and the vertex represents the maximum value of the function. The x-coordinate of the vertex is given by:
x = -b/2a
Conclusion
Quadratic equations are a fundamental concept in algebra with wide-ranging applications. Understanding their properties and methods of solving is crucial for various fields, including physics, engineering, and economics. By mastering the concepts outlined in this guide, you’ll be well-equipped to tackle quadratic equations and their applications.