Do you often ponder, What Is A Quadratic Function? At WHAT.EDU.VN, we understand that grasping mathematical concepts can sometimes feel like navigating a maze. That’s why we’re here to offer clear, accessible explanations to help you conquer any learning challenge. Join us as we explore the world of quadratic functions, unraveling their mysteries and showcasing their real-world applications. Discover the equation, explore quadratic relationships, and master quadratic expressions with ease.
1. Decoding the Quadratic Function: Unveiling the Basics
A quadratic function is essentially a polynomial function featuring one or more variables, where the highest power (exponent) of the variable is two. Simply put, it’s a polynomial function of degree 2. This means at least one term in the function must be raised to the power of 2.
Quadratic functions are ubiquitous, appearing in various fields from physics to finance. Think of the trajectory of a ball thrown in the air, the shape of a satellite dish, or the calculation of areas – all often involve quadratic functions.
2. Standard Form Unveiled: Understanding the Structure
The standard form of a quadratic function is expressed as:
f(x) = ax² + bx + c
where ‘a’, ‘b’, and ‘c’ are constants, with ‘a’ not equal to 0. The coefficient ‘a’ dictates the direction and width of the parabola, ‘b’ influences its position, and ‘c’ represents the y-intercept.
2.1. Examples of Quadratic Functions
Let’s illustrate this with some concrete examples:
- f(x) = 3x² + 5x – 2 (Here, a = 3, b = 5, and c = -2)
- f(x) = -x² + 7 (Here, a = -1, b = 0, and c = 7)
- f(x) = 2x² (Here, a = 2, b = 0, and c = 0)
However, f(x) = 5x + 1 is NOT a quadratic function because it doesn’t contain an x² term (a = 0).
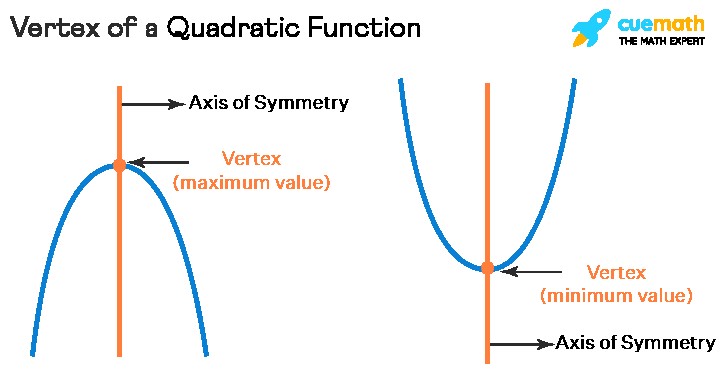
2.2. What is the Vertex of a Quadratic Function?
The vertex is the turning point of the parabola – either its lowest point (minimum) if the parabola opens upwards, or its highest point (maximum) if the parabola opens downwards. The axis of symmetry is a vertical line that passes through the vertex, dividing the parabola into two symmetrical halves. Finding the vertex is crucial for understanding the behavior and key characteristics of the quadratic function.
3. The Quadratic Formula: A Powerful Tool
The quadratic formula is a cornerstone for solving quadratic equations (ax² + bx + c = 0). It provides a direct method for finding the roots or x-intercepts of the quadratic function. The formula is:
x = [ -b ± √(b² – 4ac) ] / 2a
This formula is invaluable when factoring is difficult or impossible.
4. Exploring Different Forms: A Versatile Function
Quadratic functions can appear in three primary forms: standard form, vertex form, and intercept form. Each form reveals different aspects of the function.
- Standard Form: f(x) = ax² + bx + c (as discussed earlier)
- Vertex Form: f(x) = a(x – h)² + k, where (h, k) is the vertex of the parabola.
- Intercept Form: f(x) = a(x – p)(x – q), where p and q are the x-intercepts of the parabola.
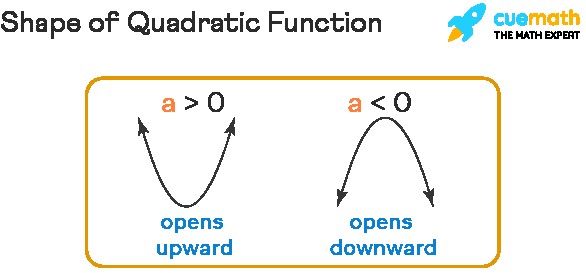
The value of ‘a’ determines whether the parabola opens upwards (a > 0) or downwards (a < 0).
4.1. Converting Between Forms
It’s possible to convert between these forms using algebraic manipulation. For instance, the vertex form is useful for quickly identifying the vertex of the parabola.
4.2. Converting Standard Form to Vertex Form
To convert from standard form (f(x) = ax² + bx + c) to vertex form (f(x) = a(x – h)² + k), we use the following formulas:
h = -b / 2a
k = f(h) = f(-b / 2a)
Example: Convert f(x) = x² + 4x – 1 to vertex form.
- a = 1, b = 4, c = -1
- h = -4 / (2 * 1) = -2
- k = f(-2) = (-2)² + 4(-2) – 1 = 4 – 8 – 1 = -5
- Therefore, the vertex form is f(x) = (x + 2)² – 5
4.3. Converting Standard Form to Intercept Form
To convert from standard form to intercept form (f(x) = a(x – p)(x – q)), find the roots (p and q) of the quadratic equation ax² + bx + c = 0. This can be achieved by factoring, using the quadratic formula, or completing the square.
Example: Convert f(x) = x² – 5x + 6 to intercept form.
- a = 1, b = -5, c = 6
- Solve x² – 5x + 6 = 0. Factoring gives (x – 2)(x – 3) = 0, so x = 2 and x = 3.
- Therefore, the intercept form is f(x) = (x – 2)(x – 3).
5. Domain and Range: Defining the Boundaries
The domain and range define the set of possible input (x) and output (y) values for the quadratic function.
5.1. Domain of Quadratic Functions
The domain of any quadratic function is all real numbers (-∞, ∞), because you can input any real number into the function and get a valid output.
5.2. Range of Quadratic Functions
The range depends on whether the parabola opens upwards or downwards and the y-coordinate of the vertex (k).
- If a > 0 (parabola opens upwards), the range is [k, ∞).
- If a < 0 (parabola opens downwards), the range is (-∞, k].
For example, if the vertex is (2, -3) and a > 0, the range is [-3, ∞).
6. Graphing Quadratic Functions: Visualizing the Parabola
Graphing a quadratic function involves plotting points to create the characteristic U-shape (parabola).
- Step 1: Find the Vertex: Determine the coordinates (h, k) of the vertex using h = -b/2a and k = f(h).
- Step 2: Create a Table of Values: Choose several x-values around the vertex and calculate the corresponding y-values.
- Step 3: Plot the Points: Plot the points from the table on a coordinate plane.
- Step 4: Draw the Parabola: Connect the points with a smooth, U-shaped curve, extending the graph on both sides.
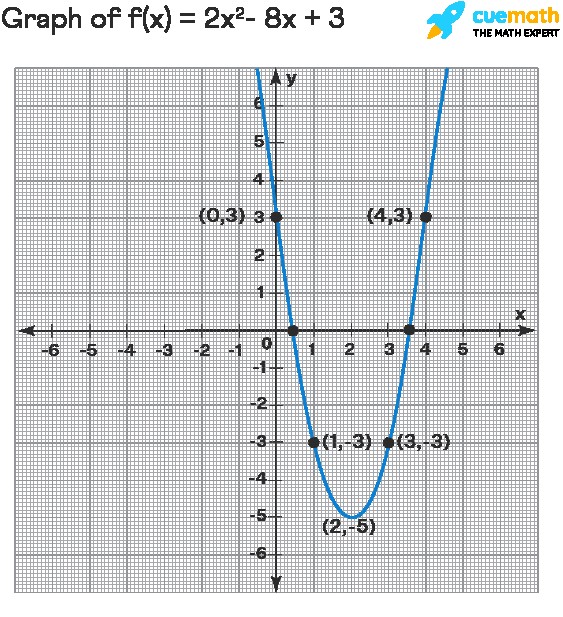
Example: Graph f(x) = x² – 2x – 3
-
Vertex: h = -(-2) / (2 * 1) = 1, k = f(1) = 1² – 2(1) – 3 = -4. Vertex is (1, -4).
-
Table of Values:
x y -1 0 0 -3 1 -4 2 -3 3 0 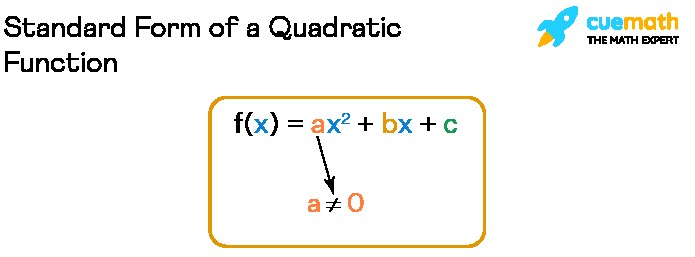
-
Plot the points and draw the parabola.
7. Maxima and Minima: Finding the Peak and Valley
Quadratic functions have either a maximum or a minimum value, which occurs at the vertex.
- If a > 0, the vertex represents the minimum value of the function.
- If a < 0, the vertex represents the maximum value of the function.
Calculus can also be used to find maxima and minima. By taking the derivative of the function, setting it equal to zero, and solving for x, you can find the x-coordinate of the vertex.
Example: Find the minimum value of f(x) = 2x² – 8x + 10.
- Take the derivative: f'(x) = 4x – 8
- Set the derivative equal to zero: 4x – 8 = 0
- Solve for x: x = 2
- Find the value of the function at x = 2: f(2) = 2(2)² – 8(2) + 10 = 2. The minimum value is 2.
8. Quadratic Function Examples
8.1. Example 1
Determine the range and vertex of the quadratic function $$f(x) = -2(x – 2)² + 4$$
Answer
To find the range and vertex of the quadratic function ( f(x) = -2(x – 2)^2 + 4 ), we can analyze the vertex form of the quadratic equation, which is given by:
$$ f(x) = a(x – h)^2 + k $$
where ( (h, k) ) is the vertex of the parabola.
In our case, the given function is:
$$ f(x) = -2(x – 2)^2 + 4 $$
Comparing this with the vertex form, we can identify the values of ( a ), ( h ), and ( k ):
- ( a = -2 )
- ( h = 2 )
- ( k = 4 )
Vertex
The vertex of the parabola is given by ( (h, k) ), so the vertex of the given quadratic function is:
$$ (2, 4) $$
Range
Since ( a = -2 ) is negative, the parabola opens downwards. This means the vertex is the maximum point of the function. Therefore, the range of the function includes all y-values less than or equal to the y-coordinate of the vertex.
The range is:
$$ (-infty, 4] $$
Conclusion
- Vertex: ( (2, 4) )
- Range: ( (-infty, 4] )
This indicates that the function has a maximum value of 4 at ( x = 2 ), and the values of ( f(x) ) extend downwards indefinitely.
8.2. Example 2
Convert the quadratic function ( f(x) = 3x^2 – 12x + 8 ) into vertex form.
Answer
To convert the quadratic function ( f(x) = 3x^2 – 12x + 8 ) into vertex form, we complete the square. The vertex form of a quadratic function is ( f(x) = a(x – h)^2 + k ), where ( (h, k) ) is the vertex.
Here’s the step-by-step conversion:
-
Factor out the coefficient of ( x^2 ) (if it’s not 1) from the ( x^2 ) and ( x ) terms:
$$ f(x) = 3(x^2 – 4x) + 8 $$
-
Complete the square inside the parentheses:
- Take half of the coefficient of ( x ) (which is -4), square it, and add and subtract it inside the parentheses.
$$ left(frac{-4}{2}right)^2 = (-2)^2 = 4 $$
So, we add and subtract 4 inside the parentheses:
$$ f(x) = 3(x^2 – 4x + 4 – 4) + 8 $$
-
Group the terms to form a perfect square trinomial:
$$ f(x) = 3((x^2 – 4x + 4) – 4) + 8 $$
-
Rewrite the perfect square trinomial as a square:
$$ f(x) = 3((x – 2)^2 – 4) + 8 $$
-
Distribute the 3 and simplify:
$$ f(x) = 3(x – 2)^2 – 12 + 8 $$
$$ f(x) = 3(x – 2)^2 – 4 $$
So, the vertex form of the quadratic function ( f(x) = 3x^2 – 12x + 8 ) is:
$$ f(x) = 3(x – 2)^2 – 4 $$
8.3. Example 3
Find the x-intercepts of the quadratic function $$f(x) = x^2 – 5x + 6$$
Answer
To find the x-intercepts of the quadratic function $$f(x) = x^2 – 5x + 6$$, we need to solve for ( x ) when ( f(x) = 0 ). This involves finding the roots of the quadratic equation $$x^2 – 5x + 6 = 0$$.
Here’s the step-by-step solution:
-
Set the quadratic function equal to zero:
$$x^2 – 5x + 6 = 0$$
-
Factor the quadratic equation:
We look for two numbers that multiply to 6 and add to -5. These numbers are -2 and -3.
So, we can factor the equation as:
$$(x – 2)(x – 3) = 0$$
-
Set each factor equal to zero and solve for ( x ):
- $$x – 2 = 0 Rightarrow x = 2$$
- $$x – 3 = 0 Rightarrow x = 3$$
Thus, the x-intercepts of the quadratic function $$f(x) = x^2 – 5x + 6$$ are $$x = 2$$ and $$x = 3$$.
Conclusion
The x-intercepts of the given quadratic function are $$x = 2$$ and $$x = 3$$. These are the points where the parabola intersects the x-axis.
9. Practice Questions on Quadratic Function
Question 1: What is the factored form of a quadratic function?
Question 2: What is the standard form of a quadratic function?
Question 3: Identify the type of x-intercepts of the quadratic equation f(x) = (x + 6)² + 2
Question 4: Determine the vertex of the quadratic equation $$f(x) = 2(x + 3)² + 2$$
Question 5: The y-intercept of the equation $$f(x) = 2(x + 3)² + 2$$ is
(Answers at the end of the article)
10. FAQs About Quadratic Functions
10.1. What is a Quadratic Function in Math?
A quadratic function is a polynomial function where the highest exponent of the variable is 2. It is expressed in the general form f(x) = ax² + bx + c, where a ≠ 0.
10.2. Why is it Called a Quadratic Function?
The term “quadratic” comes from the Latin word “quadratus,” meaning square. This refers to the fact that the highest power of the variable in the function is 2 (squared).
10.3. What is the Quadratic Function Equation?
The standard form equation of a quadratic function is f(x) = ax² + bx + c, where ‘a’, ‘b’, and ‘c’ are constants and ‘a’ is not zero.
10.4. What is the Vertex of a Quadratic Function?
The vertex is the point where the parabola changes direction. It is the minimum point if the parabola opens upwards (a > 0) or the maximum point if the parabola opens downwards (a < 0).
10.5. What are the Zeros of a Quadratic Function?
The zeros (also called roots or x-intercepts) are the points where the graph of the function intersects the x-axis (f(x) = 0).
10.6. What is a Quadratic Functions Table?
A table that displays the values of y-coordinates corresponding to various x-coordinates for a quadratic function.
10.7. How to Draw Quadratic Graph?
Plot the vertex, find additional points by plugging in x-values, and connect them with a smooth curve.
10.8. How to Find the x-intercept of a Quadratic Function?
Set the quadratic function equal to zero (f(x) = 0) and solve for x. The solutions are the x-intercepts.
10.9. Is a Parabola a Quadratic Function?
Yes, a parabola is the graphical representation of a quadratic function.
10.10. How to Find the Inverse of a Quadratic Function?
Find the inverse of a quadratic function f(x) involves swapping x and y, and solving the equation for y. Note that the inverse will not be a function unless the domain is restricted.
10.11. What are the Forms of Quadratic Function?
Standard form (f(x) = ax² + bx + c), vertex form (f(x) = a(x – h)² + k), and intercept form (f(x) = a(x – p)(x – q)).
10.12. What is the Difference Between Quadratic Function and Quadratic Equation?
A quadratic function is an expression that defines a relationship between x and y (f(x) = ax² + bx + c), while a quadratic equation sets that expression equal to zero (ax² + bx + c = 0) to find the values of x that satisfy the equation.
Conclusion
Understanding quadratic functions is crucial for success in mathematics and its applications. By mastering their forms, graphs, and properties, you gain a powerful tool for solving a wide range of problems. Remember, practice is key, so work through examples and don’t hesitate to ask questions!
At WHAT.EDU.VN, we’re committed to providing you with the resources and support you need to excel. Do you have questions lingering in your mind? Are you struggling with a particular concept? Don’t hesitate! Visit WHAT.EDU.VN today. Our team of experts is ready and waiting to provide personalized assistance, completely free of charge. We’re located at 888 Question City Plaza, Seattle, WA 98101, United States. You can also reach us on Whatsapp at +1 (206) 555-7890 or visit our website what.edu.vn. We believe that everyone deserves access to quality education, and we’re here to make learning easier and more accessible for you.
Answers to Practice Questions:
- f(x) = a(x – p)(x – q)
- f(x) = ax² + bx + c
- No x-intercepts
- (-3, 2)
- 20