In mathematics, the quotient is a fundamental concept that emerges from the operation of division. Simply put, the quotient is the result you get when you divide one number by another. It tells you how many times one number (the divisor) is contained within another number (the dividend).
For instance, if you divide 10 by 2, the quotient is 5. This means that 2 goes into 10 exactly 5 times. Quotients can be whole numbers, like in this example, or they can be decimal numbers, depending on whether the division is exact or not. Let’s delve deeper into understanding what a quotient is, how to find it, and its relationship with other essential terms in division.
Quotient Definition: The Result of Division
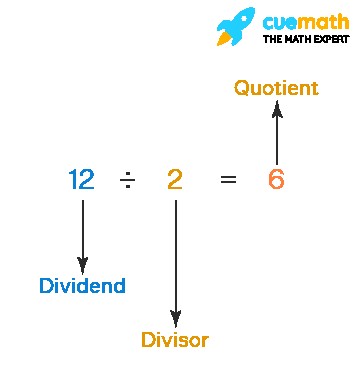
The quotient is formally defined as the numerical answer obtained after performing division. It represents the number of times the divisor is fully contained within the dividend. Consider the visual representation below to understand the relationship between the dividend, divisor, and quotient. In this example, 12 divided by 2 equals 6, where 6 is the quotient. The divisor (2) fits into the dividend (12) exactly 6 times.
It’s important to note that while the quotient can be larger or smaller than the divisor, it will always be smaller than the dividend (unless you are dividing a number by a fraction less than 1, which is a more advanced concept).
How to Calculate the Quotient: The Division Process
Finding the quotient is the primary goal of division. Division is one of the four basic operations in arithmetic, alongside addition, subtraction, and multiplication. The quotient is simply the solution you arrive at after carrying out the division process.
Sometimes, division results in a whole number quotient with no remainder, indicating an exact division. Other times, you might have a remainder left over, indicating that the division is not exact. However, even in cases with remainders, there is still a quotient which represents the whole number result of the division before considering the remainder.
Exploring Quotient, Divisor, and Dividend: Key Terms in Division
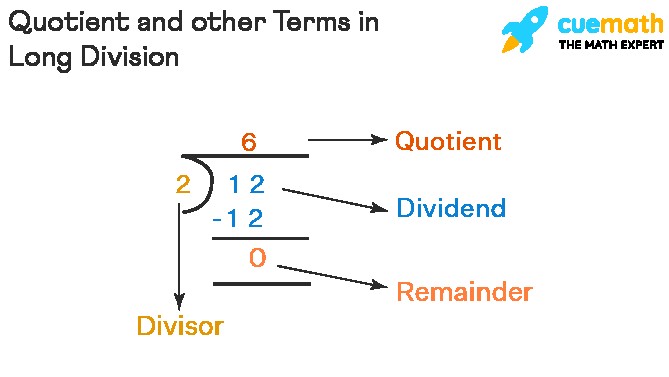
When discussing quotients, it’s essential to understand the other terms involved in division: the divisor and the dividend. Let’s illustrate these terms with a relatable example. Imagine you have 12 cookies and want to share them equally among 2 friends.
| Term | Description | Value in Cookie Example |
|---|---|---|
| Dividend | The total quantity being divided (what you start with). | 12 cookies |
| Divisor | The number of groups you are dividing into (how many to share among). | 2 friends |
| Quotient | The quantity in each group (how many each friend gets). | 6 cookies each |
| Remainder | The quantity left over after dividing equally (any leftover cookies). | 0 cookies |
In this cookie example, the division statement is 12 ÷ 2 = 6. This can be visually represented as:
Understanding Quotient and Remainder: Incomplete Division
Often, when you divide numbers, the division isn’t perfectly even, and you end up with a remainder. The remainder is the amount left over after you’ve divided as much as possible into whole groups. The quotient, in this case, still represents the whole number result of the division.
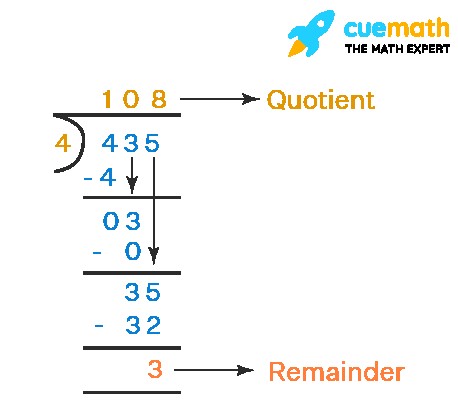
Let’s consider dividing 435 by 4. Here, 435 is the dividend and 4 is the divisor. We can use long division to find the quotient and remainder:
Step-by-step Long Division of 435 by 4:
-
Step 1: Divide the first digit of the dividend (4) by the divisor (4). 4 ÷ 4 = 1. Write ‘1’ as the first digit of the quotient above the 4. Multiply 1 by 4 and subtract the result (4) from the first digit of the dividend (4), resulting in 0. Bring down the next digit of the dividend (3) next to the 0.
-
Step 2: Now we have 03, or simply 3. Try to divide 3 by 4. Since 3 is smaller than 4, it cannot be divided to get a whole number. Write ‘0’ as the next digit of the quotient. Multiply 0 by 4 and subtract the result (0) from 3, resulting in 3. Bring down the next digit of the dividend (5) next to the 3.
-
Step 3: Now we have 35. Divide 35 by 4. The largest multiple of 4 that is less than or equal to 35 is 32 (4 x 8 = 32). Write ‘8’ as the next digit of the quotient. Multiply 8 by 4 and subtract the result (32) from 35, resulting in 3.
-
Step 4: We have reached the end of the digits in the dividend. The remaining number, 3, is the remainder because it is less than the divisor (4). The number above the division bar, 108, is the quotient.
In this example, when we divide 435 by 4, the quotient is 108 and the remainder is 3.
Verifying Division Results:
To check if your division is correct, you can use the following formula:
Dividend = (Divisor × Quotient) + Remainder
Using our example: 435 = (4 × 108) + 3. This simplifies to 435 = 432 + 3, which is 435 = 435. Since both sides are equal, our division is correct.
Estimating the Quotient: Approximations in Division
Estimating the quotient is a useful skill, especially when you need a quick, approximate answer without performing exact long division. It involves rounding the dividend and divisor to numbers that are easier to work with mentally.
Let’s estimate the quotient for 64 ÷ 22:
-
Step 1: Round the dividend (64) and the divisor (22) to the nearest ten. 64 rounds down to 60, and 22 rounds down to 20.
-
Step 2: Divide the rounded numbers: 60 ÷ 20 = 3.
Therefore, the estimated quotient for 64 ÷ 22 is approximately 3.
Another method for estimation: After rounding, you can simplify by canceling out zeros if both the rounded dividend and divisor end in zero. In our example, 60 ÷ 20 becomes 6 ÷ 2, which also equals 3.
Example of Estimating Quotient: Estimate the quotient of 825 divided by 24.
Solution:
-
Step 1: Round 825 to the nearest hundred (800) and 24 to the nearest ten (20).
-
Step 2: Divide the rounded numbers: 800 ÷ 20 = 40.
So, the estimated quotient for 825 divided by 24 is approximately 40.
Quotient Examples in Real-World Problems
Let’s look at some examples where understanding quotients is helpful:
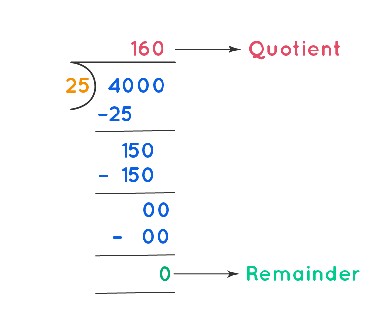
Example 1: $4000 is distributed equally among 25 workers. How much does each worker receive?
Solution: To find out how much each worker gets, we need to divide the total amount ($4000) by the number of workers (25).
The quotient is 160. Therefore, each worker receives $160.
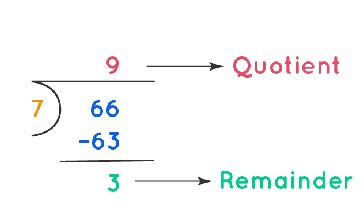
Example 2: Divide 66 by 7 and find the quotient and remainder.
Solution: Using long division for 66 ÷ 7:
The quotient is 9, and the remainder is 3.
Example 3: True or False:
a) The quotient is the final answer obtained when dividing numbers. (True)
b) A remainder is always present in division. (False) – Remainders are not present in exact divisions.
Show Answer! >Show Answer! >Show Answer! >
Practice Questions on Quotient
- Solve: 150 ÷ 10. What is the quotient?
- Divide 78 by 5 using long division. Identify the quotient and remainder.
Check Solution >Check Solution >
FAQs about Quotient
What is Quotient in Math?
In mathematics, the quotient is the answer you get after dividing one number (dividend) by another (divisor). It represents how many times the divisor fits into the dividend. For example, in 63 ÷ 9 = 7, the quotient is 7. The quotient can be a whole number or a decimal.
How to Find the Quotient in Division?
To find the quotient, you perform the division operation. The quotient is the result of this operation. Using the formula: Quotient = Dividend ÷ Divisor. For example, in 12 ÷ 4 = 3, 3 is the quotient.
Is Quotient Always a Whole Number?
No, the quotient is not always a whole number. It can be a whole number or a decimal number. If the division is exact (no remainder), the quotient will be a whole number. If there is a remainder, the quotient can be expressed as a decimal by continuing the division process. For example, 16 ÷ 2 = 8 (whole number quotient), but 16 ÷ 5 = 3.2 (decimal quotient).
What is the Difference Between Quotient and Remainder?
The quotient is the whole number result of division, representing how many times the divisor goes into the dividend completely. The remainder is the amount left over when the division is not exact. For example, when dividing 7 by 2, the quotient is 3 (2 goes into 7 three times completely), and the remainder is 1 (because 3 x 2 = 6, and 7 – 6 = 1).
How Can we Verify the Quotient in Division?
You can verify the quotient using the formula: Dividend = (Divisor × Quotient) + Remainder. If you multiply the divisor by the quotient and add the remainder, you should get the original dividend. This confirms the accuracy of your division.
How to Find the Quotient When the Remainder and Divisor is given?
If you know the dividend, divisor, and remainder, and you need to find the quotient, you can rearrange the verification formula. However, typically, if you have the divisor and dividend, you perform division to find both the quotient and remainder. If you are given the remainder and divisor and are asked to find a possible quotient, you might need more context or information about the dividend.
What is the Quotient of 21 Divided by 7?
The quotient of 21 divided by 7 is 3. (21 ÷ 7 = 3).
What is the Difference Between Quotient and Product?
Quotient is the result of division. Product is the result of multiplication. Division and multiplication are inverse operations. The quotient is generally smaller than the dividend, while the product is generally larger than the numbers being multiplied.
How to Estimate the Quotient?
To estimate the quotient, round the dividend and divisor to numbers that are easier to divide mentally. For example, to estimate 84 ÷ 18, round 84 to 80 and 18 to 20. Then divide 80 ÷ 20 = 4. The estimated quotient is 4.