Are you curious about rational functions and how they work? At WHAT.EDU.VN, we understand that grasping new mathematical concepts can sometimes feel overwhelming. That’s why we’re here to provide you with a clear and comprehensive explanation of what a rational function is, complete with examples and practical applications. Discover the world of polynomial ratios and their significance in various fields, all while enjoying a user-friendly and accessible learning experience. Looking for free answers and a community to help you learn, ask on WHAT.EDU.VN today and get the answers you need.
1. Understanding Rational Functions
A rational function is a mathematical expression representing the ratio of two polynomials. It can be written as f(x) = p(x)/q(x), where p(x) and q(x) are polynomials, and q(x) is not equal to zero. This definition is similar to that of a rational number, which is a fraction p/q where q is not zero. Rational functions are used in various fields, including describing the relationship between speed, distance, and time, as well as in the medical and engineering industries.
1.1. Polynomials in Rational Functions
Rational functions involve polynomials in both the numerator and denominator. A polynomial is an expression consisting of variables and coefficients, combined using addition, subtraction, and non-negative integer exponents. For example, x² + 3x + 2 and 5x – 7 are polynomials. The degree of a polynomial is the highest exponent of its variable. Understanding polynomials is essential for working with rational functions.
1.2. Key Characteristics of Rational Functions
Rational functions have several key characteristics:
- Ratio of Polynomials: The function is expressed as one polynomial divided by another.
- Variable Denominator: The denominator must contain a variable to differentiate it from a polynomial function.
- Domain Restrictions: The denominator cannot equal zero, leading to domain restrictions that create asymptotes.
- Asymptotes: Rational functions often have vertical, horizontal, or oblique asymptotes, which are lines that the graph approaches but never touches.
- Intercepts: Rational functions may have x-intercepts (where the graph crosses the x-axis) and y-intercepts (where the graph crosses the y-axis).
1.3. Examples of Rational Functions
Here are a few examples of rational functions:
- f(x) = (x + 1) / (x – 2)
- g(x) = (3x² – 2x + 5) / (x + 4)
- h(x) = 1 / (x² + 1)
- k(x) = (x³ – 8) / (x² + 5x + 6)
1.4. Non-Examples of Rational Functions
To better understand what rational functions are, it’s helpful to know what they are not. Here are some examples of functions that are not rational functions:
- f(x) = √x (because the numerator is not a polynomial)
- g(x) = sin(x) / x (because the numerator is not a polynomial)
- h(x) = (x + 1) / 5 (because the denominator is a constant)
- k(x) = (x + √x) / (x – 1) (because the numerator contains a non-polynomial term)
2. Identifying Rational Functions
Identifying a rational function involves checking if the function is a ratio of two polynomials. If either the numerator or the denominator is not a polynomial, the function is not rational. For example, f(x) = (4 + √x) / (2 – x) and g(x) = (3 + (1/x)) / (2 – x) are not rational functions because their numerators are not polynomials.
2.1. What to Look For
When identifying a rational function, look for the following:
- Polynomials: Both the numerator and denominator must be polynomials. This means they should only contain variables with non-negative integer exponents, coefficients, and constants.
- No Non-Polynomial Terms: Avoid functions with terms like square roots, trigonometric functions, or exponential functions in either the numerator or denominator.
- Variable in Denominator: The denominator must contain a variable. If the denominator is a constant, the function is a polynomial, not a rational function.
- Simplified Form: Ensure the function is simplified. Sometimes, a function that appears non-rational can be transformed into a rational function through algebraic manipulation.
2.2. Examples of Identifying Rational Functions
Let’s look at some examples to illustrate how to identify rational functions:
-
Example 1: f(x) = (x² + 3x + 2) / (x – 1)
This is a rational function because both the numerator (x² + 3x + 2) and the denominator (x – 1) are polynomials.
-
Example 2: g(x) = (sin(x) + 1) / (x² – 4)
This is not a rational function because the numerator (sin(x) + 1) contains a trigonometric function, which is not a polynomial.
-
Example 3: h(x) = (√x + 2) / (x + 3)
This is not a rational function because the numerator (√x + 2) contains a square root, which is not a polynomial.
-
Example 4: k(x) = (x³ – 2x + 1) / 7
This is not a rational function because the denominator (7) is a constant, and a rational function must have a variable in the denominator.
2.3. Recognizing Polynomials
To accurately identify rational functions, you need to recognize polynomials. A polynomial is an expression that can be written in the form:
a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x + a_0
Where:
a_n, a_{n-1}, ..., a_1, a_0are coefficients (constants).xis the variable.nis a non-negative integer (the degree of the term).
Examples of polynomials:
- 5x² – 3x + 7
- 2x³ + x – 4
- 9x + 2
- 6 (a constant polynomial)
Non-examples of polynomials:
x^(1/2)(fractional exponent)1/x(negative exponent)sin(x)(trigonometric function)e^x(exponential function)|x|(absolute value)
3. Domain and Range of Rational Functions
The domain of a rational function is the set of all x-values for which the function is defined. The range is the set of all possible output values (y-values) that the function can produce.
3.1. Domain of Rational Functions
The domain of a rational function includes all real numbers except those that make the denominator equal to zero. To find the domain:
- Set the denominator not equal to zero: q(x) ≠ 0
- Solve for x: Find the values of x that make the denominator zero.
- Exclude those values from the set of real numbers: The domain is all real numbers except those values.
Example: Find the domain of f(x) = (2x + 1) / (3x – 2).
Solution:
- Set the denominator not equal to zero: 3x – 2 ≠ 0
- Solve for x: 3x ≠ 2 => x ≠ 2/3
Thus, the domain is {x ∈ R | x ≠ 2/3}.
3.2. Range of Rational Functions
The range of a rational function is the set of all possible y-values. Finding the range can be more complex, but here’s a general approach:
- Replace f(x) with y: y = p(x) / q(x)
- Solve the equation for x: Express x in terms of y.
- Set the denominator of the resultant equation not equal to zero: Find the values of y that make the denominator zero.
- Exclude those values from the set of real numbers: The range is all real numbers except those values.
Example: Find the range of f(x) = (2x + 1) / (3x – 2).
Solution:
-
Replace f(x) with y: y = (2x + 1) / (3x – 2)
-
Solve for x:
(3x – 2)y = 2x + 1
3xy – 2y = 2x + 1
3xy – 2x = 2y + 1
x(3y – 2) = 2y + 1
x = (2y + 1) / (3y – 2) -
Set the denominator not equal to zero: 3y – 2 ≠ 0 => y ≠ 2/3
So the range is {y ∈ R | y ≠ 2/3}.
3.3. Practical Tips for Finding Domain and Range
Finding the domain and range of rational functions can be tricky. Here are some practical tips to help you:
- Factor the Denominator: Factoring the denominator can help you easily identify the values of x that make it zero.
- Simplify the Function: Simplifying the function by canceling common factors can make it easier to find the domain and range.
- Use Graphs: Graphing the function can provide a visual representation of the domain and range. You can see which x-values are included in the domain and which y-values are included in the range.
- Consider Asymptotes: Asymptotes often indicate the boundaries of the domain and range. Vertical asymptotes indicate values excluded from the domain, while horizontal asymptotes indicate values that the function approaches but may not reach in the range.
3.4. Domain and Range with Holes
Rational functions can sometimes have “holes,” which are points where the function is undefined but do not result in a vertical asymptote. These occur when a factor is canceled from both the numerator and denominator. When finding the domain and range, it’s important to account for these holes.
Example: Consider the function f(x) = (x² – 4) / (x – 2).
- Factor the numerator: f(x) = ((x – 2)(x + 2)) / (x – 2)
- Cancel the common factor: f(x) = x + 2, x ≠ 2
The function simplifies to f(x) = x + 2, but with a hole at x = 2.
- Domain: All real numbers except x = 2.
- Range: All real numbers except y = 4 (since when x = 2, y = 2 + 2 = 4).
4. Asymptotes of Rational Functions
A rational function can have three types of asymptotes: vertical, horizontal, and slant asymptotes. Additionally, it can have holes.
4.1. Holes of a Rational Function
Holes are points that appear to be on the graph but are not actually present. They occur when there are common factors in both the numerator and denominator.
How to Find Holes:
- Factor the numerator and denominator.
- Cancel any common factors.
- Set the canceled factors equal to zero and solve for x. These are the x-coordinates of the holes.
- Substitute the x-values into the simplified function to find the corresponding y-coordinates.
Example: Find the holes of the function f(x) = (x² + 5x + 6) / (x² + x – 2).
Solution:
-
Factorize the numerator and denominator:
f(x) = [(x + 2)(x + 3)] / [(x + 2)(x – 1)]
-
Cancel the common factor (x + 2):
f(x) = (x + 3) / (x – 1), x ≠ -2
-
Since (x + 2) was canceled, there is a hole at x = -2.
-
Find the y-coordinate: f(-2) = (-2 + 3) / (-2 – 1) = -1/3
Thus, there is a hole at (-2, -1/3).
4.2. Vertical Asymptotes
A vertical asymptote (VA) is an imaginary vertical line that the graph approaches but never touches. It is of the form x = some number.
How to Find Vertical Asymptotes:
- Simplify the function by canceling all common factors (if any).
- Set the denominator equal to zero and solve for x.
Example: Find the vertical asymptotes of the function f(x) = (x² + 5x + 6) / (x² + x – 2).
Solution:
-
We already saw that this function simplifies to f(x) = (x + 3) / (x – 1).
-
Set the denominator to 0:
x – 1 = 0 => x = 1
Thus, there is a VA at x = 1.
4.3. Horizontal Asymptotes
A horizontal asymptote (HA) is an imaginary horizontal line that the graph approaches but never touches. It is of the form y = some number.
How to Find Horizontal Asymptotes:
Compare the degrees of the numerator (N) and denominator (D):
- If N < D, then there is a HA at y = 0.
- If N > D, then there is no HA.
- If N = D, then the HA is y = (ratio of the leading coefficients).
Example: Find the horizontal asymptote (if any) of the function f(x) = (x² + 5x + 6) / (x² + x – 2).
Solution:
Here the degree of the numerator is N = 2, and the degree of the denominator is D = 2.
Since N = D, the HA is y = (leading coefficient of numerator) / (leading coefficient of denominator) = 1/1 = 1.
Thus, the HA is y = 1.
4.4. Slant (Oblique) Asymptotes
A slant asymptote is an imaginary oblique line that the graph approaches. A rational function has a slant asymptote only when the degree of the numerator (N) is exactly one greater than the degree of the denominator (D).
How to Find Slant Asymptotes:
- Divide the numerator by the denominator using long division.
- The equation of the slant asymptote is y = quotient (ignoring the remainder).
Example: Find the slant asymptote of the function f(x) = x² / (x + 1).
Solution:
Here the degree of the numerator is 2 and that of the denominator = 1. So it has a slant asymptote.
Let us divide x² by (x + 1) by long division:
Thus, the slant asymptote is y = x – 1.
5. Graphing Rational Functions
Graphing rational functions involves understanding their asymptotes, intercepts, and behavior. Here are the steps for graphing a rational function:
- Identify Asymptotes: Find and draw the vertical, horizontal, and slant asymptotes using dotted lines.
- Plot Holes: Identify and plot any holes.
- Find Intercepts: Calculate the x-intercepts (by setting y = 0) and y-intercepts (by setting x = 0) and plot them.
- Create a Table: Make a table with columns for x and y, including the x-intercepts and vertical asymptotes in the x-column. Choose additional x-values on either side of these key points.
- Compute y-values: Calculate the corresponding y-values by substituting each x-value into the function.
- Plot Points and Draw Curves: Plot all the points from the table and draw smooth curves connecting them, ensuring the curves approach the asymptotes but do not touch them.
Example: Graph the rational function f(x) = (x² + 5x + 6) / (x² + x – 2).
Solution:
-
We have already identified that its VA is x = 1, its HA is y = 1, and the hole is at (-2, -1/3). Use dotted lines for asymptotes. The simplified form of the given function is f(x) = (x + 3) / (x – 1).
-
Find the intercepts:
- For x-intercept, put y = 0. Then 0 = (x + 3) / (x – 1) => x + 3 = 0 => x = -3. So the x-intercept is at (-3, 0).
- For y-intercept, put x = 0. Then y = (0 + 3) / (0 – 1) => y = -3. So the y-intercept is at (0, -3).
-
Create a table:
| x | y |
|---|---|
| -5 | y = (-5 + 3) / (-5 – 1) = 0.33 |
| -4 | y = (-4 + 3) / (-4 – 1) = 0.2 |
| -3 | 0 (x-int) |
| -2 | y = (-2 + 3) / (-2 – 1) = -0.33 |
| 0 | -3 (y-int) |
| 1 | VA |
| 2 | y = (2 + 3) / (2 – 1) = 5 |
| 3 | y = (3 + 3) / (3 – 1) = 3 |

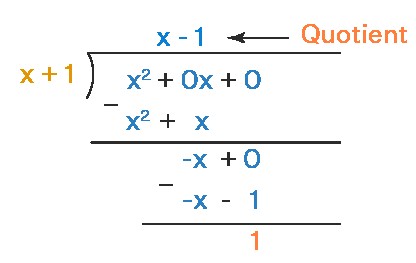

Let us plot all these points on the graph along with all asymptotes, hole, and intercepts.
5.1. Using Transformations to Graph Rational Functions
Understanding transformations can simplify the process of graphing rational functions, especially when dealing with variations of the basic function f(x) = 1/x. Transformations include shifts, stretches, compressions, and reflections.
- Vertical Shift: Adding or subtracting a constant outside the function shifts the graph vertically. For example, f(x) = (1/x) + k shifts the graph up by k units if k > 0 and down by |k| units if k < 0.
- Horizontal Shift: Adding or subtracting a constant inside the function shifts the graph horizontally. For example, f(x) = 1/(x – h) shifts the graph right by h units if h > 0 and left by |h| units if h < 0.
- Vertical Stretch/Compression: Multiplying the function by a constant stretches or compresses the graph vertically. For example, f(x) = a(1/x) stretches the graph vertically if |a| > 1 and compresses it if 0 < |a| < 1.
- Reflection: Multiplying the function by -1 reflects the graph across the x-axis. For example, f(x) = -1/x reflects the graph of f(x) = 1/x across the x-axis.
By recognizing these transformations, you can quickly sketch the graph of a rational function without plotting numerous points.
6. Inverse of a Rational Function
The inverse of a rational function y = f(x) is a function that “undoes” the original function. To find the inverse:
- Replace f(x) with y.
- Interchange x and y.
- Solve the resultant equation for y.
- The result would give the inverse f⁻¹(x).
Example: Find the inverse of the rational function f(x) = (2x – 1) / (x + 3).
Solution:
-
The given function can be written as:
y = (2x – 1) / (x + 3)
-
Interchanging x and y:
x = (2y – 1) / (y + 3)
-
Now, we will solve for y.
x(y + 3) = 2y – 1
xy + 3x = 2y – 1
3x + 1 = 2y – xy
3x + 1 = y (2 – x)
y = (3x + 1) / (2 – x) = f⁻¹(x)
6.1. Verifying the Inverse
To verify that you have found the correct inverse function, you can check that f(f⁻¹(x)) = x and f⁻¹(f(x)) = x. This confirms that the inverse function correctly “undoes” the original function.
Example: Verify that f⁻¹(x) = (3x + 1) / (2 - x) is the inverse of f(x) = (2x - 1) / (x + 3).
- Compute
f(f⁻¹(x)):
f(f⁻¹(x)) = f((3x + 1) / (2 - x)) = (2((3x + 1) / (2 - x)) - 1) / (((3x + 1) / (2 - x)) + 3)
= ((6x + 2 - (2 - x)) / (2 - x)) / ((3x + 1 + 3(2 - x)) / (2 - x))
= (7x) / (7) = x
- Compute
f⁻¹(f(x)):
f⁻¹(f(x)) = f⁻¹((2x - 1) / (x + 3)) = (3((2x - 1) / (x + 3)) + 1) / (2 - (2x - 1) / (x + 3))
= ((6x - 3 + (x + 3)) / (x + 3)) / ((2(x + 3) - (2x - 1)) / (x + 3))
= (7x) / (7) = x
Since both f(f⁻¹(x)) = x and f⁻¹(f(x)) = x, the inverse function is verified.
7. Real-World Applications of Rational Functions
Rational functions are not just abstract mathematical concepts; they have many practical applications in various fields. Understanding these applications can help you appreciate the relevance and usefulness of rational functions in real-world scenarios.
7.1. Physics
In physics, rational functions are used to describe relationships between various physical quantities. For example, the lens equation, which relates the focal length (f), object distance (u), and image distance (v) of a lens, is a rational function:
1/f = 1/u + 1/v
This equation can be rearranged to express any one of the variables in terms of the others, making it a versatile tool for analyzing optical systems.
7.2. Engineering
Engineers use rational functions to model and analyze various systems. For example, in electrical engineering, the transfer function of a circuit, which describes the relationship between the input and output signals, is often a rational function. Similarly, in mechanical engineering, rational functions can be used to model the behavior of systems involving damping and resonance.
7.3. Economics
Economists use rational functions to model various economic phenomena. For example, cost-benefit analysis often involves rational functions to compare the costs and benefits of a particular project or policy. Similarly, rational functions can be used to model supply and demand curves, which are essential for understanding market equilibrium.
7.4. Chemistry
In chemistry, rational functions are used to describe reaction rates and equilibrium constants. For example, the Michaelis-Menten equation, which describes the rate of enzyme-catalyzed reactions, is a rational function:
v = (Vmax [S]) / (Km + [S])
Where:
- v is the reaction rate
- Vmax is the maximum reaction rate
- [S] is the substrate concentration
- Km is the Michaelis constant
7.5. Medicine
In medicine, rational functions are used in dosage calculations and drug distribution models. For example, the concentration of a drug in the bloodstream over time can be modeled using a rational function, helping doctors determine the appropriate dosage and frequency of administration.
:max_bytes(150000):strip_icc():format(webp)/GettyImages-87404215-58887d455f9b58bdb35fd93f.jpg)
8. Common Mistakes to Avoid
Working with rational functions can be challenging, and it’s easy to make mistakes. Here are some common mistakes to avoid:
- Forgetting to Exclude Values from the Domain: Always remember to find the values of x that make the denominator zero and exclude them from the domain.
- Incorrectly Identifying Asymptotes: Be careful when determining the horizontal and slant asymptotes. Make sure you compare the degrees of the numerator and denominator correctly.
- Canceling Factors Incorrectly: Only cancel common factors that are present in both the numerator and denominator. Avoid canceling terms that are added or subtracted.
- Ignoring Holes: Remember to account for holes when finding the domain and range. These points are not part of the function’s graph.
- Misinterpreting Graphs: Pay attention to the behavior of the graph near the asymptotes and holes. Make sure your graph approaches the asymptotes but does not touch them.
9. Examples of Rational Functions
Example 1: Basic Rational Function
Consider the function f(x) = 1/x. This is the simplest rational function, with a vertical asymptote at x = 0 and a horizontal asymptote at y = 0. The domain is all real numbers except x = 0, and the range is all real numbers except y = 0.
Example 2: Linear over Linear
Let’s analyze the rational function f(x) = (x + 1) / (x – 2).
- Vertical Asymptote: The denominator is zero when x = 2, so there’s a vertical asymptote at x = 2.
- Horizontal Asymptote: Since the degrees of the numerator and denominator are equal, there’s a horizontal asymptote at y = 1 (ratio of leading coefficients).
- Intercepts: Setting x = 0 gives y = -1/2 (y-intercept), and setting y = 0 gives x = -1 (x-intercept).
Example 3: Quadratic over Linear
Consider the function f(x) = (x^2 – 4) / (x + 1).
- Vertical Asymptote: The denominator is zero when x = -1, so there’s a vertical asymptote at x = -1.
- Slant Asymptote: Since the degree of the numerator is one greater than the degree of the denominator, there’s a slant asymptote. Dividing (x^2 – 4) by (x + 1) gives a quotient of x – 1 and a remainder of -3. Thus, the slant asymptote is y = x – 1.
- Intercepts: Setting x = 0 gives y = -4 (y-intercept), and setting y = 0 gives x = ±2 (x-intercepts).
Example 4: Hole in a Rational Function
Consider the function f(x) = (x^2 – 9) / (x – 3).
- Simplification: This function can be simplified by factoring the numerator: f(x) = ((x – 3)(x + 3)) / (x – 3). Canceling the common factor (x – 3) gives f(x) = x + 3, but with a hole at x = 3.
- Hole: At x = 3, the function is undefined. Thus, there is a hole at (3, 6).
10. Rational Function FAQs
10.1. What is the Definition of a Rational Function?
A rational function is a function that looks like a fraction where both the numerator and denominator are polynomials. It looks like f(x) = p(x) / q(x), where both p(x) and q(x) are polynomials.
10.2. What is the End Behavior of Rational Function?
The end behavior of the parent rational function f(x) = 1/x is:
- f(x) → 0 as x → ∞ or -∞ and this corresponds to the horizontal asymptote.
- f(x) → ∞ as x → 0+ and f(x) → -∞ as x → 0- and these correspond to the vertical asymptote.
10.3. How Do You Know If a Function is Rational?
Whenever a function has polynomials in its numerator and denominator then it is a rational function. But remember:
- The numerator of a rational function can be a constant. For example: 1 / x² is a rational function.
- The denominator of a rational function cannot be a constant. For example: x² / 1 is NOT a rational function.
10.4. How to Graph a Rational Function?
To graph a rational function, first plot all the asymptotes by dotted lines. Plot the x and y-intercepts. Make a table with two columns labeled x and y. Put all x-intercepts and vertical asymptotes in the column of x. Take some random numbers on either side of each of these numbers and compute the corresponding y-values using the function. Plot all these points on the graph and join them by curves without touching the asymptotes.
10.5. How to Find the Domain and Range of a Rational Function?
To find the domain and range of a rational function:
- First, simplify the function.
- For domain, set denominator not equal to zero and solve for x.
- For range, solve the simplified equation for x, set the denominator not equal to zero, and solve for y.
10.6. How to Find Holes in Rational Functions?
To find holes, first, factorize both numerator and denominator. If any linear factors are getting canceled, just set each of them to 0 and simplify. They will give the x-coordinates of the holes. We can use the function to find the corresponding y-coordinates of holes.
10.7. How to Find Asymptotes of Rational Functions?
To find the asymptotes of a rational function:
- Simplify the function to its lowest form.
- Set the denominator = 0 and solve to find the vertical asymptotes.
- Solve the equation for x, set the denominator = 0, and solve to find horizontal asymptotes.
10.8. How to Find the Inverse of a Rational Function?
To find the inverse of a rational function y = f(x), just switch x and y first, then solve the resultant equation for y. It will give the inverse of f(x) which is represented as f⁻¹(x).
10.9. What are the Applications of Rational Function?
Rational functions are used to model many real-life scenarios. In particular, they are used in the fields of business, science, and medicine.
We hope this comprehensive guide has helped you understand rational functions. Whether you’re a student tackling homework or someone curious about mathematical applications, rational functions play a significant role in many fields.
Still have questions or need more clarification? Don’t hesitate to ask your questions on WHAT.EDU.VN. We provide a free platform for you to ask any question and receive quick, accurate answers from knowledgeable individuals. Visit WHAT.EDU.VN today and experience the ease of getting your queries resolved. Contact us at 888 Question City Plaza, Seattle, WA 98101, United States, or reach out via WhatsApp at +1 (206) 555-7890. Let what.edu.vn be your go-to resource for all your questions.