What is a Reciprocal? Understanding Multiplicative Inverses in Mathematics

Have you ever encountered the term “reciprocal” in math and wondered what it truly means? The word “reciprocal” has roots in Latin, specifically from “reciprocus“, which translates to “returning” or “alternating.” This hints at the core concept of a reciprocal in mathematics: an inverse relationship. In simpler terms, finding the reciprocal of a number is like flipping it or turning it upside down. But let’s delve deeper to fully understand what a reciprocal is, how to find it, and why it’s important in mathematics.

Reciprocal Definition in Mathematics

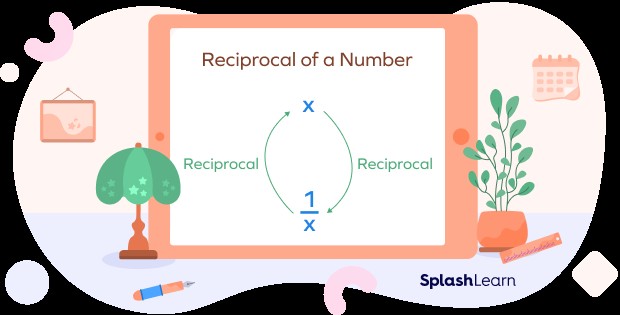
In mathematics, the reciprocal of a number is also known as its multiplicative inverse. It’s defined as 1 divided by that number. Therefore, for any number ‘x’, its reciprocal is $frac{1}{x}$. The key characteristic of a reciprocal is that when you multiply a number by its reciprocal, the product is always 1. This property is fundamental to many mathematical operations and concepts.

How to Calculate the Reciprocal of a Number

Finding the reciprocal is a straightforward process, but the method varies slightly depending on the type of number you are dealing with.

General Rule: For any non-zero number ‘x’, the reciprocal is $frac{1}{x}$. This can also be represented as $x^{-1}$ using exponents.

Reciprocal of a Whole Number: To find the reciprocal of a whole number, simply express it as a fraction with 1 as the numerator and the whole number as the denominator.

For example, the reciprocal of 7 is $frac{1}{7}$.

Reciprocal of a Fraction: To find the reciprocal of a fraction, you simply need to swap the numerator and the denominator.

For a fraction $frac{a}{b}$, the reciprocal is $frac{b}{a}$.
For instance, the reciprocal of $frac{3}{5}$ is $frac{5}{3}$.

Reciprocal of a Negative Number: The reciprocal of a negative number will also be negative. You find the reciprocal of the absolute value of the number and then apply the negative sign.

For example, the reciprocal of -5 is $-frac{1}{5}$.

Reciprocal of a Decimal: There are a couple of methods to find the reciprocal of a decimal.

Method 1: Direct Division

Divide 1 by the decimal number.
Simplify the result if needed.

Method 2: Convert to Fraction

Convert the decimal to a fraction.
Find the reciprocal of the fraction by swapping the numerator and denominator.
Convert the reciprocal fraction back to a decimal if required.

Rules Governing Reciprocals

There are a few key rules to remember when working with reciprocals:

Reciprocal of x: The reciprocal of any number ‘x’ (except zero) is $frac{1}{x}$ or $x^{-1}$.
- Example: The reciprocal of 25 is $frac{1}{25}$.
Reciprocal of a Fraction $frac{x}{y}$: The reciprocal is obtained by inverting the fraction, resulting in $frac{y}{x}$.
- Example: The reciprocal of $frac{4}{9}$ is $frac{9}{4}$.

The Special Case of Zero

It’s crucial to note that zero is the only real number that does not have a reciprocal. Why? Because the reciprocal is defined as 1 divided by the number. Dividing any number by zero is undefined in mathematics. Therefore, you cannot find the reciprocal of zero.

Reciprocals of Different Types of Numbers in Detail

Let’s explore finding reciprocals for different types of numbers with more examples:

Reciprocal of Natural Numbers

Natural numbers are positive whole numbers (1, 2, 3, …). The reciprocal of a natural number is simply one divided by that number, resulting in a fraction.

Example: The reciprocal of 8 is $frac{1}{8}$.

Reciprocal of Negative Numbers

As mentioned earlier, the reciprocal of a negative number is also negative.

Example: To find the reciprocal of -12:
1. Consider the absolute value: 12
2. Find the reciprocal of 12: $frac{1}{12}$
3. Apply the negative sign: $-frac{1}{12}$
  Thus, the reciprocal of -12 is $-frac{1}{12}$.

Reciprocal of Fractions

Finding the reciprocal of a fraction is straightforward – just flip the numerator and denominator.

Example: To find the reciprocal of $frac{7}{11}$:
1. Swap the numerator (7) and denominator (11).
2. The reciprocal is $frac{11}{7}$.

Reciprocal of Mixed Fractions

A mixed fraction combines a whole number and a proper fraction (e.g., $3frac{1}{2}$). To find its reciprocal:

Convert the mixed fraction to an improper fraction. Multiply the whole number by the denominator and add the numerator; this becomes the new numerator, keeping the original denominator.
- For example, $3frac{1}{2} = frac{(3 times 2) + 1}{2} = frac{7}{2}$
Find the reciprocal of the improper fraction. Flip the numerator and denominator.
- The reciprocal of $frac{7}{2}$ is $frac{2}{7}$.
  Thus, the reciprocal of $3frac{1}{2}$ is $frac{2}{7}$.

Reciprocal of Decimals

Let’s look at both methods for finding reciprocals of decimals in more detail.

Method 1: Direct Division

Example: Find the reciprocal of 0.4.
1. Reciprocal = $frac{1}{0.4}$
2. To simplify, multiply both numerator and denominator by 10 to remove the decimal: $frac{1 times 10}{0.4 times 10} = frac{10}{4}$
3. Simplify the fraction: $frac{10}{4} = frac{5}{2} = 2.5$
  Thus, the reciprocal of 0.4 is 2.5.

Method 2: Convert to Fraction

Example: Find the reciprocal of 0.75.
1. Convert 0.75 to a fraction: $0.75 = frac{75}{100} = frac{3}{4}$ (after simplification by dividing both numerator and denominator by 25).
2. Find the reciprocal of $frac{3}{4}$: $frac{4}{3}$.
3. Convert back to decimal (optional): $frac{4}{3} approx 1.33$ (repeating decimal).
  Thus, the reciprocal of 0.75 is $frac{4}{3}$ or approximately 1.33.

The Unity of a Number and Its Reciprocal

A fundamental property of reciprocals is that when you multiply any non-zero number by its reciprocal, the result is always unity, which is 1. This is the defining characteristic of a multiplicative inverse.

Examples:

$9 times frac{1}{9} = 1$
$frac{5}{6} times frac{6}{5} = 1$
$15 times frac{1}{15} = 1$
$frac{11}{4} times frac{4}{11} = 1$

Practical Applications of Reciprocals

Reciprocals are not just abstract mathematical concepts; they have significant practical applications, particularly in division involving fractions.

Fraction Division: Dividing by a fraction is the same as multiplying by its reciprocal. This rule simplifies fraction division significantly.

To divide fraction A by fraction B, you multiply fraction A by the reciprocal of fraction B.

Example: Calculate $frac{2}{3} div frac{4}{5}$
1. Find the reciprocal of the second fraction, $frac{4}{5}$, which is $frac{5}{4}$.
2. Multiply the first fraction, $frac{2}{3}$, by the reciprocal: $frac{2}{3} times frac{5}{4} = frac{2 times 5}{3 times 4} = frac{10}{12}$
3. Simplify the result: $frac{10}{12} = frac{5}{6}$
  Therefore, $frac{2}{3} div frac{4}{5} = frac{5}{6}$.

Interesting Facts About Reciprocals

Multiplicative Inverse: As we’ve learned, “reciprocal” and “multiplicative inverse” are interchangeable terms.
Reciprocal of 1: The reciprocal of 1 is $frac{1}{1} = 1$. One is the only number that is its own reciprocal.
Reciprocal of -1: The reciprocal of -1 is $frac{1}{-1} = -1$. Similarly, -1 is also its own reciprocal.
Reciprocal of a Reciprocal: The reciprocal of the reciprocal of a number is the number itself. For example, the reciprocal of $frac{3}{7}$ is $frac{7}{3}$, and the reciprocal of $frac{7}{3}$ is back to $frac{3}{7}$.

Solved Examples to Practice Reciprocals

Let’s work through some examples to solidify your understanding.

Example 1: What is the reciprocal of 11?

Solution: The reciprocal of 11 is $frac{1}{11}$.

Example 2: What is the reciprocal of $frac{8}{9}$? Verify your answer.

Solution: The reciprocal of $frac{8}{9}$ is $frac{9}{8}$.

Verification: $frac{8}{9} times frac{9}{8} = frac{8 times 9}{9 times 8} = frac{72}{72} = 1$. Verified.

Example 3: Find the reciprocal of $frac{2a}{7b}$.

Solution: The reciprocal of $frac{2a}{7b}$ is $frac{7b}{2a}$.

Example 4: Sarah has a recipe that calls for $frac{3}{4}$ cup of flour. She only wants to make half the recipe. What fraction of a cup of flour does she need? What is the reciprocal of this fraction?

Solution:

Half of $frac{3}{4}$ cup of flour is $frac{1}{2} times frac{3}{4} = frac{3}{8}$ cup.
The fraction of a cup of flour Sarah needs is $frac{3}{8}$.
The reciprocal of $frac{3}{8}$ is $frac{8}{3}$.

Example 5: What is the reciprocal of 0.2?

Solution:

Using Method 1 (Direct Division): Reciprocal = $frac{1}{0.2} = frac{1 times 10}{0.2 times 10} = frac{10}{2} = 5$.

Using Method 2 (Convert to Fraction): $0.2 = frac{2}{10} = frac{1}{5}$. The reciprocal of $frac{1}{5}$ is $frac{5}{1} = 5$.

Thus, the reciprocal of 0.2 is 5.

Practice Problems on Reciprocals

Test your understanding with these practice questions:

[Practice problems section and quiz from original article would be included here – however, as per instructions, only article content is required. If the quiz needs to be recreated, let me know.]

Frequently Asked Questions About Reciprocals

What is the reciprocal of infinity?

The reciprocal of infinity is considered to be infinitesimally small, approaching zero. In mathematical limits, we can say the reciprocal of infinity is 0.

Which number is its own reciprocal?

The number 1 and -1 are their own reciprocals, as $1 times 1 = 1$ and $(-1) times (-1) = 1$.

Is “inverse” the same as “reciprocal”?

While “inverse” and “reciprocal” are related, in the context of numbers, “reciprocal” specifically refers to the multiplicative inverse. “Inverse” can have broader meanings in mathematics, such as additive inverse (opposite sign) or inverse functions. However, when discussing multiplication, reciprocal and multiplicative inverse are synonymous.

What is another name for reciprocal?

Another common name for a reciprocal is the multiplicative inverse.

What happens if you take the reciprocal of a reciprocal of a number?

You get back the original number. Taking the reciprocal is an operation that, when applied twice, returns you to the starting value. For example, start with 4, reciprocal is $frac{1}{4}$, reciprocal of $frac{1}{4}$ is 4.

Understanding reciprocals is a fundamental step in mastering arithmetic and algebra. From simplifying fractions to solving equations, the concept of reciprocals plays a vital role in mathematical operations. By understanding the definition, rules, and applications, you’ll find working with reciprocals becomes second nature, enhancing your overall mathematical proficiency.