What Is A Rectangle? It’s a fundamental geometric shape, and at WHAT.EDU.VN, we’re dedicated to providing clear and concise answers to all your questions. A rectangle, a type of quadrilateral, is a closed, two-dimensional shape with four straight sides, four right angles (90 degrees), and equal and parallel opposite sides. Understanding this definition opens the door to exploring its unique properties, real-world applications, and relationship to other geometric shapes like squares and parallelograms. Want to learn more? WHAT.EDU.VN offers a platform to ask any question and get answers on geometric shapes, mathematical concepts, and other intriguing topics.
1. Defining the Rectangle: Key Characteristics
A rectangle is more than just a four-sided shape. Several key characteristics define it:
1.1 Four Sides (Quadrilateral)
Like all quadrilaterals, a rectangle has four sides. These sides are line segments that connect to form a closed figure. Without four sides, the shape wouldn’t be a rectangle.
1.2 Four Right Angles
This is a crucial characteristic. Each of the four interior angles of a rectangle measures exactly 90 degrees. This “right angle” is what distinguishes a rectangle from a general parallelogram.
1.3 Opposite Sides Equal and Parallel
The two pairs of opposite sides in a rectangle are both equal in length and parallel to each other. Parallel lines never intersect, no matter how far they are extended.
1.4 Two Dimensions: Length and Width
Rectangles exist in two dimensions. The longer side is typically referred to as the “length,” and the shorter side is the “width.” These two measurements define the size and proportions of the rectangle.
2. Understanding the Properties of a Rectangle
Knowing the defining characteristics leads us to understand the unique properties of rectangles.
2.1 Angles
As mentioned earlier, all four angles are right angles (90 degrees). This means the sum of all interior angles in a rectangle is always 360 degrees (4 x 90 = 360).
2.2 Sides
Opposite sides are congruent (equal in length) and parallel. Adjacent sides (sides that share a vertex) are perpendicular to each other, forming the right angles.
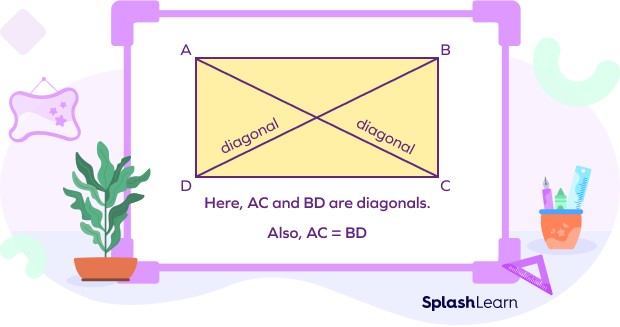
2.3 Diagonals
Diagonals are line segments that connect opposite vertices (corners) of the rectangle.
- Congruent Diagonals: The two diagonals of a rectangle are always equal in length.
- Bisect Each Other: The diagonals bisect each other, meaning they intersect at their midpoint. This point is the center of the rectangle.
- Do Not Intersect at Right Angles: Unlike a square, the diagonals of a rectangle (unless it’s a square) do not intersect at a 90-degree angle.
2.4 Symmetry
A rectangle possesses two lines of symmetry. Each line runs through the midpoint of a pair of opposite sides.
3. Rectangles vs. Other Quadrilaterals: A Comparison
Rectangles belong to the broader family of quadrilaterals. Understanding their relationship to other quadrilaterals helps clarify their definition.
3.1 Square
A square is a special type of rectangle. It possesses all the properties of a rectangle (four sides, four right angles, opposite sides equal and parallel) but with an additional constraint: all four sides must be equal in length. Therefore, every square is a rectangle, but not every rectangle is a square.
3.2 Parallelogram
A parallelogram is a quadrilateral with opposite sides parallel. A rectangle is a special type of parallelogram where all angles are right angles. Thus, every rectangle is a parallelogram, but not every parallelogram is a rectangle.
3.3 Rhombus
A rhombus is a quadrilateral with all four sides equal in length. While a square is both a rectangle and a rhombus, a general rhombus does not have right angles, so it’s not a rectangle.
3.4 Trapezoid (or Trapezium)
A trapezoid is a quadrilateral with at least one pair of parallel sides. A rectangle has two pairs of parallel sides, making it a special type of trapezoid.
3.5 General Quadrilateral
A general quadrilateral is simply any four-sided shape. It has no specific requirements for angles or side lengths. A rectangle is a highly specific type of quadrilateral with many constraints.
| Shape | Definition | Properties |
|---|---|---|
| Rectangle | Four sides, four right angles, opposite sides equal and parallel | Congruent diagonals that bisect each other; two lines of symmetry |
| Square | Four sides, four right angles, all sides equal | All properties of a rectangle plus diagonals intersect at right angles; four lines of symmetry |
| Parallelogram | Four sides, opposite sides parallel | Opposite sides congruent; opposite angles congruent; diagonals bisect each other |
| Rhombus | Four sides, all sides equal | Opposite angles congruent; diagonals bisect each other at right angles |
| Trapezoid | Four sides, at least one pair of parallel sides | No specific angle or side requirements beyond having four sides and one pair of parallel sides |
| Quadrilateral | Four sides | No specific angle or side requirements |



4. Formulas for Rectangles: Area and Perimeter
Two fundamental measurements associated with rectangles are area and perimeter.
4.1 Area
The area of a rectangle represents the amount of surface it covers. It’s calculated by multiplying its length (l) by its width (w):
*Area = l w**
The area is always expressed in square units (e.g., square inches, square meters, square feet).
4.2 Perimeter
The perimeter of a rectangle is the total distance around its outside. It’s calculated by adding up the lengths of all four sides. Since opposite sides are equal, the formula can be simplified to:
Perimeter = 2l + 2w or Perimeter = 2(l + w)
The perimeter is expressed in linear units (e.g., inches, meters, feet).
5. Real-World Examples of Rectangles
Rectangles are ubiquitous in our daily lives. Here are just a few examples:
5.1 Architecture and Construction
- Buildings: Most rooms in houses and buildings are rectangular.
- Doors and Windows: Doors and windows are typically rectangular.
- Bricks and Tiles: Many construction materials, like bricks and tiles, are rectangular.
5.2 Technology
- Screens: Computer screens, TVs, smartphones, and tablets all have rectangular displays.
- Laptops: The overall shape of a laptop is often rectangular.
- Keyboards: The keys on a keyboard are generally rectangular.
5.3 Everyday Objects
- Books: The pages of a book and the book itself are usually rectangular.
- Tables: Table tops are often rectangular.
- Paper: Standard sheets of paper are rectangular.
- Playing Cards: Most playing cards are rectangular.
- Envelopes: Envelopes come in various sizes, but they are generally rectangular.
- Currency: Banknotes (paper money) are rectangular.
5.4 Sports
- Playing Fields: Many sports fields, such as basketball courts, tennis courts, and swimming pools, are rectangular.
6. How to Determine if a Shape is a Rectangle
If you need to determine whether a shape is a rectangle, you can use the following methods:
6.1 Measure the Angles
Use a protractor or a set square to measure each of the four angles. If all four angles are 90 degrees, the shape could be a rectangle.
6.2 Measure the Sides
Measure the lengths of all four sides.
- If all four sides are equal: The shape is a square (which is also a rectangle).
- If opposite sides are equal: The shape is likely a rectangle or a parallelogram.
6.3 Check for Parallel Sides
Use a ruler and set square to check if opposite sides are parallel.
6.4 Check the Diagonals
Draw the diagonals of the quadrilateral.
- Measure the lengths of the diagonals: If they are equal, the shape could be a rectangle.
- Check if the diagonals bisect each other: If they do, the shape is likely a rectangle or a parallelogram.
- Check if the diagonals intersect at a right angle: If they do, the shape is a square (which is also a rectangle).
6.5 Combine Measurements and Observations
The most reliable way to confirm if a shape is a rectangle is to combine measurements and observations. For example, confirm that the shape has four sides, four right angles, and that opposite sides are equal and parallel.
7. Advanced Concepts Involving Rectangles
Beyond the basics, rectangles are used in various advanced mathematical and scientific concepts.
7.1 Coordinate Geometry
In coordinate geometry, rectangles can be defined by their vertices. Calculations such as area and perimeter can be performed using coordinate geometry formulas.
7.2 Calculus
Rectangles are used in calculus to approximate the area under a curve using Riemann sums.
7.3 Linear Algebra
Matrices can be used to represent transformations such as scaling, rotation, and shearing, which can change the dimensions and orientation of rectangles in space.
7.4 Physics
Rectangular shapes are often used in physics to model various phenomena, such as the distribution of forces on a rectangular surface or the flow of fluids through a rectangular channel.
7.5 Engineering
Engineers use rectangles in various applications, such as designing structures, calculating stress and strain, and optimizing the use of materials.
8. Fun Facts About Rectangles
- A rectangle is also known as an equiangular quadrilateral because all its angles are equal.
- The word “rectangle” comes from the Latin words “rectus” (right) and “angulus” (angle).
- Rectangles are used extensively in art and design to create balanced and harmonious compositions.
- The Golden Rectangle is a rectangle whose sides are in the golden ratio (approximately 1.618). It is considered aesthetically pleasing and has been used in art and architecture for centuries.
9. Solved Examples
Let’s look at some solved examples to reinforce our understanding of rectangles.
9.1 Example 1: Identifying Rectangles
Which of the following shapes are rectangles?
Solution:
Shapes A and D are rectangles. They have four sides, four right angles, and opposite sides are equal and parallel.
9.2 Example 2: Finding Length, Width, and Diagonals
Identify the length, width, and diagonals in the given rectangle.
Solution:
- Length: PQ and RS
- Width: SP and RQ
- Diagonals: PR and QS
9.3 Example 3: Calculating Perimeter
The length and width of a rectangle are 7 inches and 21 inches respectively. Find its perimeter.
Solution:
Perimeter of a rectangle = 2 × (Length + Width)
= 2 × (7 + 21) inches
= 2 × (28) inches
= 56 inches
9.4 Example 4: Calculating Area
The length and width of a rectangle are 0.3 m and 15 cm. Find its area.
Solution:
Length = 0.3 m and Width = 15 cm
First, convert the length to centimeters: 0.3 m = 30 cm
Area = length × width = 30 cm × 15 cm = 450 cm²
9.5 Example 5: Finding the Diagonal
Find the length of the diagonal of a rectangle whose sides are 8 inches and 6 inches.
Solution:
Length of the diagonal = √(length² + width²) = √(8² + 6²) = √(64 + 36) = √100 = 10 inches
10. Practice Problems
Test your knowledge with these practice problems.
10.1 Problem 1
What is the area of a rectangular cardboard 1 m long and 30 cm wide?
a) 30 sq. cm
b) 300 sq. cm
c) 3,000 sq. cm
d) 30,000 sq. cm
Answer: c) 3,000 sq. cm
10.2 Problem 2
What is the perimeter of a rectangle with length 16 feet and width 7 feet?
a) 23 feet
b) 46 feet
c) 112 feet
d) 305 feet
Answer: b) 46 feet
10.3 Problem 3
What is the width of the rectangle whose length and area are 8 cm and 32 cm² respectively?
a) 256 cm
b) 4 cm
c) 40 cm
d) 80 cm
Answer: b) 4 cm
11. Frequently Asked Questions (FAQs) About Rectangles
Here are some common questions about rectangles.
11.1 What is the definition of a rectangle?
A rectangle is a closed 2-D shape with four sides, four corners, and four right angles (90°). The opposite sides of a rectangle are equal and parallel.
11.2 What are some real-life examples of a rectangle?
Some real-life examples of a rectangle include books, doors, tabletops, blackboards, and screens.
11.3 What is the difference between a rectangle and a parallelogram?
A rectangle is a special type of parallelogram where all angles are right angles. A parallelogram only requires opposite sides to be parallel and equal.
11.4 Why are all rectangles not squares?
All rectangles are not squares because a rectangle only requires opposite sides to be equal, while a square requires all sides to be equal. A square has the additional constraint of all sides being equal, which is not a requirement for rectangles.
11.5 Can a rectangle be a kite?
No, a rectangle cannot be a kite. A kite is a quadrilateral with two pairs of adjacent sides that are equal in length. In a rectangle, opposite sides are equal, not adjacent sides.
11.6 How do you find the area of a rectangle?
The area of a rectangle is found by multiplying its length by its width: Area = Length × Width.
11.7 How do you find the perimeter of a rectangle?
The perimeter of a rectangle is found by adding up the lengths of all its sides, or by using the formula: Perimeter = 2 × (Length + Width).
11.8 What is a golden rectangle?
A golden rectangle is a rectangle whose sides are in the golden ratio (approximately 1.618). It is considered aesthetically pleasing and has been used in art and architecture for centuries.
11.9 What are the properties of the diagonals of a rectangle?
The diagonals of a rectangle are congruent (equal in length) and bisect each other. They do not intersect at right angles unless the rectangle is a square.
11.10 What is the sum of the interior angles of a rectangle?
The sum of the interior angles of a rectangle is always 360 degrees because it is a quadrilateral.
12. Further Exploration and Resources
To deepen your understanding of rectangles, consider exploring these resources:
- Geometry textbooks: Consult geometry textbooks for detailed explanations and proofs.
- Online geometry resources: Websites like Khan Academy and Math is Fun offer comprehensive lessons and interactive exercises.
- Interactive geometry software: Use software like GeoGebra to construct and manipulate rectangles and explore their properties.
- Real-world observations: Pay attention to rectangular shapes in your environment and analyze their properties.
13. Still Have Questions? Ask WHAT.EDU.VN
Do you still have burning questions about rectangles or any other topic? Don’t hesitate! WHAT.EDU.VN is here to provide you with fast, accurate, and free answers. We understand the frustration of searching endlessly for reliable information. That’s why we’ve created a platform where you can ask anything and connect with knowledgeable individuals who are eager to help.
At WHAT.EDU.VN, we are committed to:
- Providing a Free Service: Ask as many questions as you like without any cost.
- Delivering Quick and Accurate Answers: Our team strives to provide you with the information you need as efficiently as possible.
- Offering Easy-to-Understand Explanations: We break down complex topics into simple, digestible language.
- Connecting You with a Knowledgeable Community: Learn from others and share your expertise.
- Ensuring a User-Friendly Platform: Our website is designed for easy navigation and a seamless experience.
We know how challenging it can be to find reliable answers, especially when facing deadlines or complex problems. Instead of struggling alone, let WHAT.EDU.VN be your go-to resource.
Ready to get your questions answered?
Visit us at WHAT.EDU.VN today and experience the ease and convenience of free knowledge!
Contact Us:
- Address: 888 Question City Plaza, Seattle, WA 98101, United States
- WhatsApp: +1 (206) 555-7890
- Website: WHAT.EDU.VN
We’re here to help you learn and grow! Ask your question on what.edu.vn now!