What Is A Scalene Triangle? This is a common geometry question, and WHAT.EDU.VN is here to provide a comprehensive answer. We’ll break down the scalene triangle definition, explore its properties, and provide examples. Looking for clear, concise answers to your geometry questions? You’ve come to the right place for triangle characteristics and angle relationships.
1. Understanding the Scalene Triangle Definition
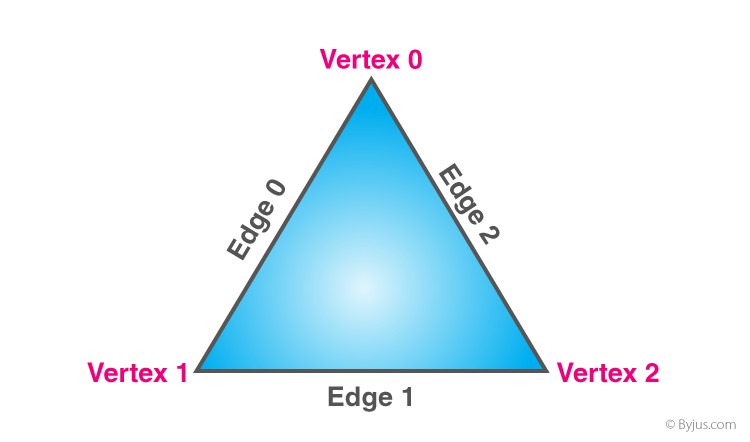
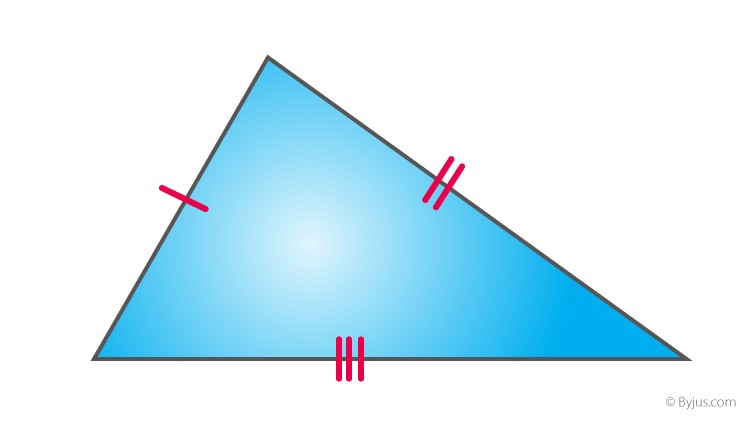
A scalene triangle is a triangle with all three sides of different lengths. Consequently, all three angles are also different in measure. This distinguishes it from other types of triangles, such as isosceles triangles (which have two equal sides) and equilateral triangles (which have all three sides equal).
Alt text: Scalene triangle diagram illustrating unequal sides and angles with labeled vertices and edges.
1.1 Key Characteristics of a Scalene Triangle
- Unequal Sides: No two sides of a scalene triangle are the same length.
- Unequal Angles: All three angles have different measures.
- No Symmetry: A scalene triangle possesses no lines of symmetry.
1.2 Angle Sum Property
Like all triangles, a scalene triangle adheres to the angle sum property, meaning that the sum of its three interior angles always equals 180 degrees. This fundamental rule applies regardless of the specific side lengths or angle measures.
2. Types of Triangles: A Quick Review
To fully grasp the concept of a scalene triangle, it’s helpful to review the classification of triangles based on both their sides and angles.
2.1 Classification by Sides
- Scalene Triangle: All three sides are different lengths.
- Isosceles Triangle: Two sides are equal in length.
- Equilateral Triangle: All three sides are equal in length.
2.2 Classification by Angles
- Acute Triangle: All three angles are less than 90 degrees.
- Right Triangle: One angle is exactly 90 degrees.
- Obtuse Triangle: One angle is greater than 90 degrees.
3. Delving Deeper: Types of Scalene Triangles
While all scalene triangles share the characteristic of unequal sides, they can be further categorized based on their angles.
3.1 Acute-Angled Scalene Triangle
An acute-angled scalene triangle has all three angles measuring less than 90 degrees. In this type of triangle, the circumcenter (the center of the circle that passes through all three vertices) lies inside the triangle.
3.2 Obtuse-Angled Scalene Triangle
An obtuse-angled scalene triangle contains one angle that measures greater than 90 degrees. In this case, the circumcenter lies outside the triangle.
3.3 Right-Angled Scalene Triangle
A right-angled scalene triangle has one angle that measures exactly 90 degrees (a right angle). The circumcenter of a right-angled scalene triangle is located at the midpoint of the hypotenuse (the side opposite the right angle).
Alt text: Illustration of a scalene triangle showcasing its distinct, unequal side lengths and angles.
4. Properties of Scalene Triangles: A Detailed Look
Scalene triangles possess several unique properties that set them apart from other triangle types. Understanding these properties is crucial for solving geometric problems and developing a deeper understanding of triangle relationships.
4.1 Key Properties Summarized
- No Equal Sides: As the defining characteristic, no two sides of a scalene triangle are equal in length.
- No Equal Angles: Consequently, no two angles are equal in measure.
- No Line of Symmetry: Scalene triangles lack any lines of symmetry. You cannot fold a scalene triangle along any line and have the two halves match perfectly.
- No Point Symmetry: Similarly, scalene triangles do not exhibit point symmetry (also known as rotational symmetry of order 2).
- Variable Angles: The angles within a scalene triangle can be acute, obtuse, or right angles, leading to the different types of scalene triangles discussed earlier.
- Circumcenter Location: The location of the circumcenter (the center of the circle that passes through all three vertices) depends on the angles of the triangle:
- Acute Scalene Triangle: Circumcenter lies inside the triangle.
- Obtuse Scalene Triangle: Circumcenter lies outside the triangle.
- Right Scalene Triangle: Circumcenter lies at the midpoint of the hypotenuse.
5. Scalene, Isosceles, and Equilateral Triangles: A Comparative Analysis
To solidify your understanding of scalene triangles, it’s helpful to compare them to isosceles and equilateral triangles. The following table highlights the key differences:
| Feature | Scalene Triangle | Isosceles Triangle | Equilateral Triangle |
|---|---|---|---|
| Side Lengths | All three sides are unequal | Two sides are equal | All three sides are equal |
| Angle Measures | All three angles are different | Two angles are equal (opposite the equal sides) | All three angles are equal (60 degrees each) |
| Symmetry | No lines of symmetry | One line of symmetry | Three lines of symmetry |
6. Mastering the Formulas: Area and Perimeter of a Scalene Triangle
Calculating the area and perimeter of a scalene triangle requires specific formulas. Let’s explore these formulas in detail.
6.1 Area of a Scalene Triangle
There are two primary methods for calculating the area of a scalene triangle, depending on the information available:
6.1.1 Base and Height Method
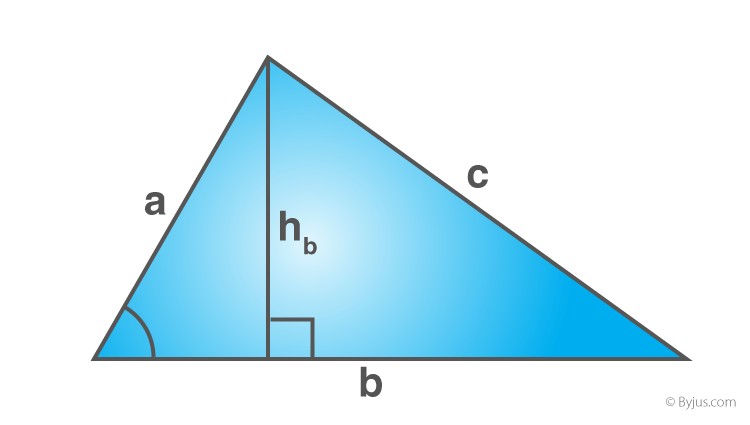
If you know the base (b) and height (h) of the triangle, you can use the following formula:
Area = (1/2) x b x h square units
Where:
- “b” refers to the base of the triangle (the side perpendicular to the height).
- “h” refers to the height of the triangle (the perpendicular distance from the base to the opposite vertex).
6.1.2 Heron’s Formula
If you know the lengths of all three sides (a, b, c), you can use Heron’s formula:
Area = √[s(s-a)(s-b)(s-c)] square units
Where:
- s is the semi-perimeter of the triangle, calculated as: s = (a + b + c) / 2
- a, b, and c are the lengths of the three sides of the triangle.
Alt text: Scalene triangle area formula using base, height and Heron’s formula with semi-perimeter calculation.
6.2 Perimeter of a Scalene Triangle
The perimeter of any triangle, including a scalene triangle, is simply the sum of the lengths of its three sides:
Perimeter = a + b + c units
Where:
- a, b, and c are the lengths of the three sides of the triangle.
7. Real-World Application: Solved Examples
Let’s solidify your understanding with a couple of solved examples:
Example 1: Finding the Area Using Heron’s Formula
Problem: Find the area of a scalene triangle ABC with sides of length 8 cm, 6 cm, and 4 cm.
Solution:
- Identify the side lengths: a = 8 cm, b = 6 cm, c = 4 cm
- Calculate the semi-perimeter (s):
s = (a + b + c) / 2 = (8 + 6 + 4) / 2 = 9 cm - Apply Heron’s Formula:
Area = √[s(s-a)(s-b)(s-c)] = √[9(9-8)(9-6)(9-4)] = √(9 1 3 * 5) = √135 ≈ 11.6 cm²
Therefore, the area of the scalene triangle is approximately 11.6 cm².
Example 2: Finding the Perimeter
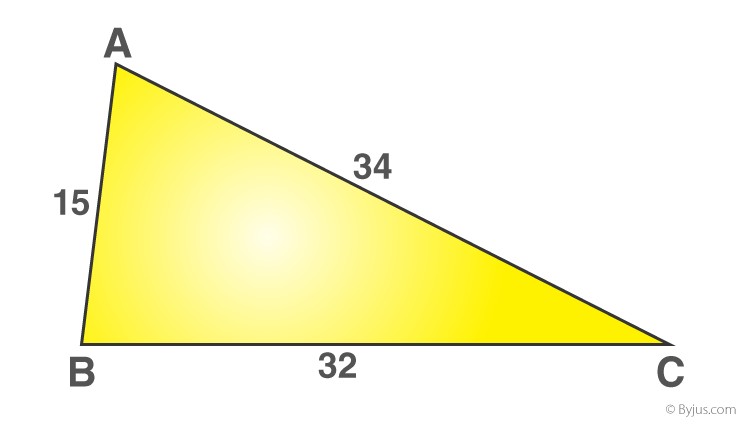
Problem: The sides of a triangle are 9 cm, 13 cm, and 14 cm. Find its perimeter.
Solution:
- Identify the side lengths: a = 9 cm, b = 13 cm, c = 14 cm
- Calculate the perimeter:
Perimeter = a + b + c = 9 + 13 + 14 = 36 cm
Therefore, the perimeter of the triangle is 36 cm.
Alt text: Calculation diagram of the perimeter for a scalene triangle with sides measuring 15cm, 34cm and 32cm
8. Scalene Triangle FAQs
Still have questions about scalene triangles? Here are some frequently asked questions to further clarify the concept:
8.1 What are scalene triangles?
Scalene triangles are triangles where all three sides have different lengths, and consequently, all three angles have different measures.
8.2 What is the unique property of the scalene triangle?
The defining characteristic of a scalene triangle is that all its sides are of different lengths. This also means it lacks any lines of symmetry. Its interior angles can be acute, obtuse, or a right angle.
8.3 Does the scalene triangle obey the angle-sum property?
Yes, like all triangles, a scalene triangle adheres to the angle-sum property. The sum of its three interior angles always equals 180 degrees.
8.4 What is a right-scalene triangle?
A right-scalene triangle is a scalene triangle that contains one right angle (an angle that measures 90 degrees). The other two angles must be acute, and all three sides must be of different lengths.
8.5 What is the area and perimeter of scalene triangle?
The area of a scalene triangle can be calculated using either the formula (1/2) x base x height, if you know the base and height, or Heron’s formula if you know the lengths of all three sides. The perimeter is simply the sum of the lengths of its three unequal sides.
9. Need More Answers? Ask WHAT.EDU.VN!
Do you still have burning questions about scalene triangles or any other topic? Don’t struggle to find answers on your own! At WHAT.EDU.VN, we provide a platform where you can ask any question and receive quick, accurate, and free answers from knowledgeable individuals.
We understand the challenges of finding reliable information and the frustration of unanswered questions. That’s why we’ve created a user-friendly platform designed to connect you with experts and provide the answers you need. Whether you’re a student tackling a tough assignment, a professional seeking insights, or simply a curious individual eager to learn, WHAT.EDU.VN is here to help.
9.1 Why Choose WHAT.EDU.VN?
- Free to Use: Our platform is completely free to use. Ask as many questions as you like without any hidden fees or subscriptions.
- Fast and Accurate Answers: We strive to provide quick and accurate answers to your questions. Our community of experts is dedicated to providing helpful and reliable information.
- Easy to Use: Our platform is designed to be intuitive and user-friendly. Simply type in your question and let our system connect you with the right experts.
- Community-Driven: WHAT.EDU.VN is a community-driven platform. You can connect with other users, share your knowledge, and learn from others.
- Comprehensive Coverage: We cover a wide range of topics, from math and science to history and the arts. No matter what your question is, we’re here to help.
9.2 Don’t Hesitate – Ask Now!
Stop wasting time searching endlessly for answers. Visit WHAT.EDU.VN today and ask your question. Our team of experts is ready to provide you with the information you need. Get the clarity you deserve and unlock a world of knowledge with WHAT.EDU.VN.
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: what.edu.vn
