What Is A Sphere? This comprehensive guide from WHAT.EDU.VN explores the sphere definition, its properties, and practical applications. Do you have questions about geometry, shapes, or math in general? We provide the answers you need, and we make it easy and free to get help. Learn about spherical geometry, surface area, and volume!
1. Understanding the Definition of a Sphere
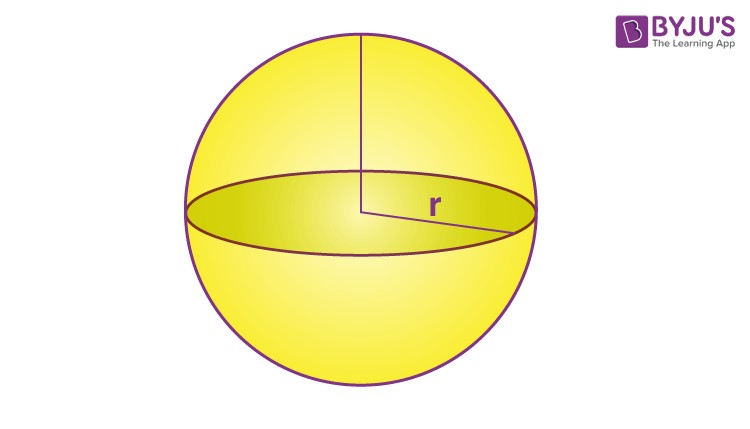
A sphere is a perfectly round geometrical object in three-dimensional space. Imagine a ball; that’s essentially a sphere! More formally, a sphere is the set of all points that are equidistant from a given point in space. This given point is the center of the sphere, and the distance from the center to any point on the sphere’s surface is called the radius. Unlike other 3D shapes, a sphere has no edges, vertices, or flat faces.
1.1 Key Characteristics
- Roundness: A sphere is perfectly round in all directions.
- Three-Dimensional: It exists in 3D space, unlike a circle which is 2D.
- Equidistant Points: Every point on the surface is the same distance from the center.
- No Edges or Vertices: It lacks the edges and corners found in polyhedra like cubes or pyramids.
- Symmetry: Spheres exhibit perfect symmetry.
1.2 Spheres in the Real World
Spheres are everywhere around us. Consider these examples:
- Planets: Earth, Mars, and other planets are approximately spherical.
- Balls: Basketballs, soccer balls, and tennis balls are designed as spheres.
- Globes: These models of Earth represent its spherical shape.
- Bubbles: Soap bubbles naturally form spheres due to surface tension.
- Certain Fruits: Oranges and grapefruits are close to spherical.
2. Core Components of a Sphere
To fully understand a sphere, it’s essential to know its key components: the radius, diameter, center, surface area, and volume.
2.1 Radius
The radius (r) is the distance from the center of the sphere to any point on its surface. It’s a fundamental measurement used in all sphere-related calculations.
2.2 Diameter
The diameter (d) is the distance across the sphere, passing through the center. It’s simply twice the radius (d = 2r).
2.3 Center
The center is the single point inside the sphere from which all points on the surface are equidistant.
2.4 Surface Area
The surface area (SA) is the total area of the sphere’s outer surface. The formula for the surface area of a sphere is SA = 4πr².
2.5 Volume
The volume (V) is the amount of space enclosed within the sphere. The formula for the volume of a sphere is V = (4/3)πr³.
3. Exploring the Properties of Spheres
Spheres have unique properties that distinguish them from other geometric shapes. These include symmetry, constant curvature, and their relationship to surface area and volume.
3.1 Symmetry
A sphere possesses a high degree of symmetry. It looks the same from every direction. This symmetry simplifies many calculations and makes spheres ideal for various applications.
3.2 Constant Curvature
The curvature of a sphere is constant at every point on its surface. This means that a sphere curves away from any tangent plane at the same rate, regardless of the point of tangency.
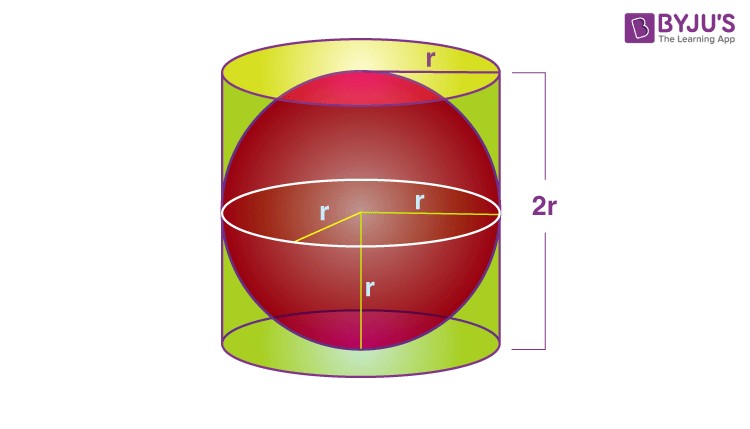
3.3 Minimal Surface Area
For a given volume, a sphere has the smallest possible surface area compared to any other shape. This property is significant in physics and engineering, where minimizing surface area can reduce energy consumption or material costs.
3.4 Maximized Volume
Conversely, for a given surface area, a sphere encloses the maximum possible volume compared to any other shape.
4. Sphere Formulas and Calculations
Understanding and applying sphere formulas is vital in various scientific and engineering fields. Here are the key formulas:
4.1 Surface Area Formula
The surface area (SA) of a sphere is calculated using the formula:
SA = 4πr²
Where:
SA= Surface areaπ(pi) ≈ 3.14159r= Radius of the sphere
This formula reveals that the surface area is directly proportional to the square of the radius.
4.2 Volume Formula
The volume (V) of a sphere is calculated using the formula:
V = (4/3)πr³
Where:
V= Volumeπ(pi) ≈ 3.14159r= Radius of the sphere
The volume is proportional to the cube of the radius, making the radius a critical parameter in determining a sphere’s size.
4.3 Diameter Formula
The diameter (d) of a sphere is simply twice the radius:
d = 2r
This relationship is straightforward but essential for converting between radius and diameter in calculations.
4.4 Circumference Formula
The circumference (C) of a sphere, measured around its widest point, is calculated as:
C = 2πr
Where:
C= Circumferenceπ(pi) ≈ 3.14159r= Radius of the sphere
5. Real-World Applications of Spheres
Spheres are not just abstract geometric shapes; they have countless practical applications in various fields.
5.1 Engineering and Architecture
- Domes: Spherical domes are used in architecture for their structural strength and ability to cover large areas without internal supports.
- Pressure Vessels: Spherical tanks are often used to store high-pressure gases or liquids because they distribute stress evenly.
- Ball Bearings: These reduce friction in machinery by providing smooth rolling contact.
5.2 Science and Technology
- Satellites: Communication and weather satellites are often spherical or nearly spherical to maintain a consistent orientation in space.
- Microscopic Particles: Many viruses and nanoparticles are spherical, influencing their behavior and interactions.
- Telescopes: Spherical mirrors are used in some telescope designs to focus light.
5.3 Everyday Life
- Sports Equipment: Balls used in sports like basketball, soccer, and volleyball are spherical for consistent performance.
- Containers: Spherical containers are sometimes used for storing liquids or powders.
- Decorative Items: Spheres are used as decorative elements in homes and gardens.
5.4 Navigation
- GPS Systems: The Earth’s nearly spherical shape is crucial for global positioning systems (GPS) to accurately determine locations.
- Astronomy: Spherical coordinates are used to map the positions of stars and other celestial objects.
6. Delving Deeper: Advanced Concepts
For those interested in a more in-depth understanding, here are some advanced concepts related to spheres:
6.1 Spherical Geometry
Spherical geometry is the study of geometry on the surface of a sphere. It differs from Euclidean geometry in several ways, such as the fact that there are no parallel lines on a sphere.
6.2 Spherical Coordinates
Spherical coordinates are a three-dimensional coordinate system used to locate points in space using a radius, an azimuthal angle (θ), and a polar angle (φ).
6.3 Sphere Packing
Sphere packing is the problem of arranging identical spheres in a given space so as to maximize the fraction of space occupied by the spheres. This has applications in materials science and coding theory.
6.4 Great Circles
A great circle is the intersection of a sphere and a plane that passes through the center of the sphere. Great circles represent the shortest distance between two points on a sphere’s surface and are important in navigation.
7. Differentiating Spheres from Circles
It’s easy to confuse spheres and circles, but they are fundamentally different. A circle is a two-dimensional shape defined by its radius, area, and circumference, whereas a sphere is a three-dimensional object possessing volume and surface area.
| Feature | Circle | Sphere |
|---|---|---|
| Dimension | Two-dimensional (2D) | Three-dimensional (3D) |
| Key Properties | Area, circumference, radius | Volume, surface area, radius |
| Representation | Flat shape | Solid object |
| Example | A coin | A ball |
8. Practical Examples and Solved Problems
Let’s solve some practical problems to solidify your understanding of sphere formulas.
8.1 Example 1: Calculating Surface Area
A sphere has a radius of 5 cm. Calculate its surface area.
-
Solution:
- Given: radius (r) = 5 cm
- Formula: SA = 4πr²
- SA = 4 3.14159 (5 cm)²
- SA = 4 3.14159 25 cm²
- SA ≈ 314.16 cm²
Therefore, the surface area of the sphere is approximately 314.16 square centimeters.
8.2 Example 2: Calculating Volume
A sphere has a radius of 8 inches. Calculate its volume.
-
Solution:
- Given: radius (r) = 8 inches
- Formula: V = (4/3)πr³
- V = (4/3) 3.14159 (8 inches)³
- V = (4/3) 3.14159 512 inches³
- V ≈ 2144.66 inches³
Therefore, the volume of the sphere is approximately 2144.66 cubic inches.
8.3 Example 3: Finding Radius from Surface Area
A sphere has a surface area of 452.39 square meters. Find its radius.
-
Solution:
- Given: SA = 452.39 m²
- Formula: SA = 4πr²
- Rearrange for r: r = √(SA / (4π))
- r = √(452.39 m² / (4 * 3.14159))
- r = √(452.39 m² / 12.56636)
- r ≈ √36 m²
- r ≈ 6 m
Therefore, the radius of the sphere is approximately 6 meters.
8.4 Example 4: Finding Diameter from Volume
A sphere has a volume of 904.78 cubic feet. Find its diameter.
-
Solution:
- Given: V = 904.78 ft³
- Formula: V = (4/3)πr³
- Rearrange for r: r = ∛((3V) / (4π))
- r = ∛((3 904.78 ft³) / (4 3.14159))
- r = ∛(2714.34 ft³ / 12.56636)
- r ≈ ∛216 ft³
- r ≈ 6 ft
- Diameter = 2r = 2 * 6 ft = 12 ft
Therefore, the diameter of the sphere is approximately 12 feet.
9. Common Misconceptions About Spheres
-
Misconception 1: Spheres and Circles are the Same: As mentioned earlier, circles are 2D while spheres are 3D.
-
Misconception 2: A Sphere is Just a Round Ball: While many balls are spherical, the term “sphere” has a precise mathematical definition related to equidistant points from a center.
-
Misconception 3: All Planets are Perfect Spheres: Planets are often oblate spheroids, slightly flattened at the poles due to their rotation.
10. Frequently Asked Questions (FAQs) about Spheres
| Question | Answer |
|---|---|
| What is a sphere? | A sphere is a perfectly round three-dimensional object in which every point on its surface is equidistant from its center. |
| What are the key properties of a sphere? | The key properties include its radius, diameter, surface area, and volume. It is also perfectly symmetrical and has a constant curvature. |
| How do you calculate the surface area of a sphere? | The surface area (SA) of a sphere is calculated using the formula SA = 4πr², where r is the radius of the sphere and π (pi) is approximately 3.14159. |
| How do you calculate the volume of a sphere? | The volume (V) of a sphere is calculated using the formula V = (4/3)πr³, where r is the radius of the sphere and π (pi) is approximately 3.14159. |
| What’s the difference between a sphere and a circle? | A circle is a two-dimensional shape with properties like area and circumference, while a sphere is a three-dimensional object with properties like volume and surface area. |
| What are some real-world examples of spheres? | Examples include planets, balls (like basketballs and soccer balls), globes, and bubbles. |
| What is spherical geometry? | Spherical geometry is the study of geometric shapes and their properties on the surface of a sphere. It differs from Euclidean geometry and is used in navigation, astronomy, and other fields. |
| What is a great circle? | A great circle is the intersection of a sphere and a plane that passes through the center of the sphere. It represents the shortest distance between two points on the sphere’s surface. |
| How are spheres used in engineering? | Spheres are used in engineering for domes, pressure vessels, ball bearings, and other applications due to their structural strength and ability to distribute stress evenly. |
| How does the Earth’s shape relate to GPS systems? | The Earth’s nearly spherical shape is crucial for global positioning systems (GPS) to accurately determine locations. GPS satellites use the Earth’s curvature to calculate distances and positions. |
11. Need More Answers? Ask WHAT.EDU.VN!
Do you still have burning questions about spheres or any other topic? Don’t hesitate to reach out to WHAT.EDU.VN!
We understand the challenges students, professionals, and curious minds face when seeking quick, reliable answers. That’s why we’ve created a platform that connects you with experts ready to provide clear, concise explanations on a wide range of subjects.
11.1 Our Commitment to You
- Free Question Submission: Ask any question, no matter how simple or complex, completely free of charge.
- Fast and Accurate Answers: Our team of knowledgeable contributors works diligently to provide you with timely and precise responses.
- Easy-to-Understand Explanations: We prioritize clarity and avoid jargon, ensuring our answers are accessible to everyone.
- A Growing Community: Join a community of learners and experts, fostering an environment of knowledge sharing and discovery.
11.2 How to Get Started
- Visit our website: WHAT.EDU.VN
- Submit your question through our easy-to-use form.
- Receive a notification when your answer is ready.
- Explore our extensive knowledge base for answers to common questions.
11.3 Contact Information
We’re here to help! You can reach us through the following channels:
- Address: 888 Question City Plaza, Seattle, WA 98101, United States
- WhatsApp: +1 (206) 555-7890
- Website: WHAT.EDU.VN
Don’t let your curiosity go unanswered. Submit your questions to what.edu.vn today and unlock a world of knowledge!
