What Is A Vertex In Math? It’s a fundamental concept, crucial for understanding shapes and structures. At WHAT.EDU.VN, we break down complex mathematical ideas like vertices into easy-to-understand explanations, ensuring everyone, from students to lifelong learners, can grasp these concepts. Dive in to explore the world of vertices, angular points and nodal points, and discover how they shape our understanding of geometry and beyond.
1. Defining the Vertex: The Cornerstones of Shapes
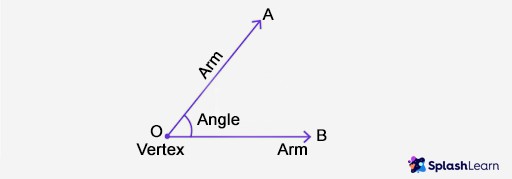
The vertex, in mathematics, is a fundamental concept across various branches of geometry and related fields. A vertex represents a point where two or more curves, lines, or edges meet. This meeting point is crucial in defining the shape and properties of geometric figures. Understanding what a vertex is, along with its attributes and applications, can help in grasping complex geometrical and mathematical problems.
1.1. Vertex: More Than Just a Point
A vertex is more than just a mere dot in a diagram. It is a critical component of any shape, defining its angles and structure. Consider a polygon, a closed figure made up of line segments. Each point where two line segments meet is a vertex. Similarly, in three-dimensional shapes, vertices are the points where edges converge to form corners. It’s worth noting that the term “vertex” is singular, while “vertices” is the plural form.
1.2. What is the Significance of Vertices in Geometry?
Vertices are essential in geometry because they help define the shape and characteristics of geometric figures. Here’s why they are significant:
- Defining Shapes: Vertices determine the shape of polygons and polyhedra. For example, a triangle has three vertices, a square has four, and so on.
- Angle Formation: Vertices are the points where angles are formed. The angle between two edges meeting at a vertex is a crucial property of the shape.
- Structural Integrity: In 3D objects, vertices contribute to the structural integrity of the object. Their placement and number affect the object’s stability and appearance.
- Mathematical Calculations: Vertices are used in various mathematical calculations, such as finding the area and volume of shapes.
For more in-depth understanding and to explore related concepts, you can always turn to resources like those available at WHAT.EDU.VN, where experts are ready to answer your questions and provide clarity.
2. History and Evolution of the Vertex Concept
The concept of the vertex has ancient roots, dating back to the early days of geometry. Its evolution reflects the development of mathematical thought and understanding of shapes and space.
2.1. Ancient Origins
The notion of a vertex can be traced back to ancient civilizations such as the Egyptians and Babylonians. These cultures used geometric principles for land surveying, construction, and astronomy. Though they may not have formally defined the term “vertex” as we know it today, they were certainly aware of the importance of corners and points in geometric shapes.
2.2. Euclidean Geometry
The formal study of vertices gained prominence with Euclidean geometry, which was systematized by the Greek mathematician Euclid around 300 BCE. Euclid’s “Elements” provided a comprehensive treatment of geometry, including definitions, postulates, and theorems related to points, lines, and shapes. Vertices were implicitly recognized as key components of polygons and polyhedra, although the term “vertex” itself may not have been explicitly defined in the same way we use it today.
2.3. Development and Refinement
Over the centuries, mathematicians refined and expanded the understanding of vertices. In the Renaissance and early modern periods, mathematicians such as René Descartes and Pierre de Fermat developed analytic geometry, which combined algebra and geometry. This allowed vertices to be represented using coordinates, facilitating calculations and analysis.
2.4. Modern Mathematics
Today, vertices play a central role in various areas of mathematics, including topology, graph theory, and computer graphics. In topology, vertices are studied in the context of abstract shapes and spaces. In graph theory, vertices are fundamental elements of graphs, representing nodes or points in a network. In computer graphics, vertices are used to define the shape and appearance of three-dimensional models.
3. Key Features Defining a Vertex
Understanding the features of a vertex is crucial to identifying and working with it in mathematical and geometric contexts. Here are some key features that define a vertex:
3.1. Intersection of Lines or Curves
A vertex is formed when two or more lines or curves intersect at a common point. This intersection creates an angle, which is an essential property of the vertex. In polygons, the vertex is where two sides meet, forming an interior angle. In three-dimensional figures, multiple sides and edges can intersect at one point, forming a vertex with multiple angles.
3.2. Angle Formation
The formation of an angle is a critical aspect of a vertex. The angle between two lines or curves meeting at a vertex determines the shape and characteristics of the geometric figure. Different types of angles, such as acute, obtuse, right, and reflex angles, can be formed at a vertex, depending on the intersection of the lines or curves.
3.3. Location and Coordinates
In coordinate geometry, vertices are identified by their location in a coordinate system. Each vertex is assigned coordinates, such as (x, y) in two-dimensional space or (x, y, z) in three-dimensional space. These coordinates allow for precise calculations and analysis of the properties of the geometric figure.
3.4. Role in Shape Definition
Vertices play a crucial role in defining the shape of geometric figures. The number and arrangement of vertices determine whether a figure is a triangle, square, pentagon, or any other polygon. In three-dimensional figures, vertices define the corners and edges of the object, contributing to its overall shape and structure.
3.5. Vertex in Different Dimensions
Vertices can exist in different dimensions, from two-dimensional shapes to three-dimensional objects. In two-dimensional shapes, vertices are points on a plane where edges meet. In three-dimensional objects, vertices are points in space where edges intersect, forming corners.
4. Vertices in 2D Figures
In two-dimensional geometry, a vertex is a corner where two edges meet. The vertex is a fundamental component of polygons, which are closed figures formed by straight line segments.
4.1. Polygons and Vertices
Polygons are characterized by the number of vertices they have. For example:
- Triangle: A triangle has three vertices, each formed by the intersection of two sides.
- Quadrilateral: A quadrilateral has four vertices, with squares, rectangles, and parallelograms being common examples.
- Pentagon: A pentagon has five vertices, each where two sides meet to form an angle.
- Hexagon: A hexagon has six vertices, and so on.
Each vertex in a polygon contributes to the shape and properties of the figure.
4.2. Circles and Vertices
Unlike polygons, a circle does not have any vertices. A circle is a curved shape with no straight edges or corners. Therefore, there are no points where two edges meet to form a vertex.
4.3. Irregular Shapes and Vertices
Irregular shapes, also known as non-regular polygons, can have vertices that are not uniform or symmetrical. The angles and side lengths may vary, but each point where two edges meet is still considered a vertex.
4.4. How to Identify Vertices in 2D Figures
Identifying vertices in 2D figures is straightforward:
- Look for Corners: Vertices are located at the corners of the shape.
- Count the Edges: Count the number of edges or sides. Each edge meets at a vertex.
- Check for Intersections: Ensure that each vertex is formed by the intersection of two straight lines.
Understanding how to identify vertices in 2D figures is essential for solving geometric problems and understanding shape properties. If you’re looking for personalized help or have questions, don’t hesitate to ask at WHAT.EDU.VN, where experts are available to assist you.
5. Vertices in 3D Figures
In three-dimensional geometry, a vertex is a point where three or more edges meet to form a corner. Understanding vertices in 3D figures is crucial for comprehending the structure and properties of solid shapes.
5.1. Polyhedra and Vertices
Polyhedra are three-dimensional solids with flat faces and straight edges. Vertices in polyhedra are the points where the edges and faces meet. Some common examples include:
- Cube: A cube has eight vertices, each formed by the intersection of three edges.
- Tetrahedron: A tetrahedron has four vertices, each formed by the intersection of three edges.
- Octahedron: An octahedron has six vertices, each formed by the intersection of four edges.
- Pyramid: A pyramid has a base with vertices and an apex, which is also a vertex.
5.2. Curved Shapes and Vertices
Not all three-dimensional shapes have vertices. For example, a sphere, cylinder, and cone have curved surfaces and do not have edges that meet at distinct points. However, a cone is an exception as it has one vertex at its apex.
5.3. Euler’s Formula
Euler’s formula relates the number of vertices (V), edges (E), and faces (F) of a polyhedron:
V - E + F = 2This formula is a fundamental concept in topology and is useful for verifying the properties of polyhedra.
5.4. Identifying Vertices in 3D Figures
Identifying vertices in 3D figures involves:
- Counting Corners: Count the number of corners where edges meet.
- Checking Intersections: Ensure that each vertex is formed by the intersection of edges.
- Using Euler’s Formula: Verify the relationship between vertices, edges, and faces using Euler’s formula.
6. Properties and Characteristics of a Vertex
Understanding the properties and characteristics of a vertex is essential for working with geometric figures. Here are some key properties:
6.1. Vertex Angle
The vertex angle is the angle formed at the vertex by the intersection of two lines or edges. The measure of the vertex angle is a crucial property of the vertex and the shape it is part of. Different types of angles, such as acute, obtuse, right, and reflex angles, can be formed at a vertex, depending on the intersection of the lines or edges.
6.2. Adjacent Vertices
Adjacent vertices are vertices that are directly connected by an edge. In a polygon, each vertex has two adjacent vertices. Understanding adjacent vertices is important for analyzing the structure and properties of geometric figures.
6.3. Non-Adjacent Vertices
Non-adjacent vertices are vertices that are not directly connected by an edge. In a polygon with more than three vertices, there are non-adjacent vertices. Diagonals can be drawn between non-adjacent vertices, which can be useful for dividing the polygon into smaller shapes.
6.4. Convex and Concave Vertices
In a polygon, a vertex can be either convex or concave:
- Convex Vertex: A vertex is convex if the interior angle at the vertex is less than 180 degrees.
- Concave Vertex: A vertex is concave if the interior angle at the vertex is greater than 180 degrees.
Concave vertices are also known as reflex vertices. Polygons with at least one concave vertex are called concave polygons, while polygons with only convex vertices are called convex polygons.
6.5. Coplanar Vertices
Coplanar vertices are vertices that lie on the same plane. In three-dimensional geometry, vertices of a flat face are coplanar. Coplanarity is an important property when analyzing the spatial relationships between vertices in 3D figures.
7. Real-World Applications of Vertices
The concept of vertices is not limited to theoretical mathematics; it has numerous real-world applications in various fields. Here are some notable examples:
7.1. Architecture and Construction
In architecture and construction, vertices are essential for designing and building structures. Architects use vertices to define the corners, edges, and intersections of buildings, ensuring structural integrity and aesthetic appeal. The placement and arrangement of vertices affect the stability and appearance of the structure.
7.2. Computer Graphics and Animation
In computer graphics and animation, vertices are used to create three-dimensional models and animations. Each vertex is defined by its coordinates in space, and the connections between vertices define the shape and surface of the object. Computer graphics software uses algorithms to render and manipulate these vertices, creating realistic images and animations.
7.3. Engineering Design
In engineering design, vertices are used to define the shape and properties of mechanical components and structures. Engineers use vertices to create precise models of objects, allowing them to analyze their performance and optimize their design. Vertices are also used in finite element analysis (FEA) to simulate the behavior of structures under different conditions.
7.4. Geographic Information Systems (GIS)
In geographic information systems (GIS), vertices are used to represent geographic features, such as points, lines, and polygons. Vertices define the location and shape of these features, allowing GIS software to analyze and visualize spatial data. Vertices are also used in mapping applications to create accurate representations of the Earth’s surface.
7.5. Game Development
In game development, vertices are used to create the environments, characters, and objects in video games. Game developers use vertices to define the shape and appearance of in-game assets, and vertices are manipulated in real-time to create dynamic and interactive experiences.
8. How to Calculate the Number of Vertices
Calculating the number of vertices in a geometric figure depends on the type of figure. Here are some common methods:
8.1. Polygons
In a polygon, the number of vertices is equal to the number of sides. For example, a triangle has three vertices, a quadrilateral has four vertices, a pentagon has five vertices, and so on. To find the number of vertices in a polygon, simply count the number of sides.
8.2. Polyhedra
In a polyhedron, the number of vertices can be calculated using Euler’s formula:
V - E + F = 2Where:
- V is the number of vertices
- E is the number of edges
- F is the number of faces
To find the number of vertices, rearrange the formula:
V = E - F + 2Count the number of edges and faces, and then use the formula to calculate the number of vertices.
8.3. Graphs
In graph theory, a graph consists of vertices (nodes) and edges. The number of vertices in a graph is simply the number of nodes in the graph. To find the number of vertices, count the number of nodes.
8.4. Complex Shapes
For complex shapes, it may be necessary to manually count the number of vertices. Look for the points where edges meet and count them carefully. It may be helpful to break the shape down into simpler components and count the vertices in each component separately.
8.5. Using Software
Software tools like CAD (Computer-Aided Design) programs can automatically calculate the number of vertices in a geometric figure. These tools can also provide other useful information, such as the coordinates of the vertices and the lengths of the edges.
9. Common Mistakes to Avoid When Working with Vertices
Working with vertices can sometimes be confusing, and it’s easy to make mistakes. Here are some common mistakes to avoid:
9.1. Confusing Vertices with Other Points
A common mistake is confusing vertices with other points in a geometric figure. Vertices are specifically the points where edges meet, forming corners. Other points, such as midpoints or centroids, are not vertices.
9.2. Miscounting Vertices
Miscounting vertices is another common mistake, especially in complex shapes. It’s important to carefully count the number of points where edges meet, and to avoid double-counting or missing any vertices.
9.3. Applying Incorrect Formulas
Applying incorrect formulas can lead to errors when calculating the number of vertices. Make sure to use the appropriate formula for the type of geometric figure you are working with. For example, use Euler’s formula for polyhedra, but not for polygons.
9.4. Ignoring Concave Vertices
Ignoring concave vertices is a mistake that can affect the accuracy of your calculations and analysis. Concave vertices have interior angles greater than 180 degrees and should be counted as vertices just like convex vertices.
9.5. Not Checking Your Work
Not checking your work is a general mistake that can lead to errors in any mathematical problem. Always double-check your calculations and make sure that your results make sense in the context of the problem.
10. Frequently Asked Questions (FAQs) about Vertices
To further clarify the concept of vertices, here are some frequently asked questions:
10.1. What is a vertex in math?
A vertex is a point where two or more lines, curves, or edges meet. In polygons, vertices are the corners where sides intersect. In polyhedra, vertices are the points where edges and faces meet.
10.2. How many vertices does a circle have?
A circle has no vertices because it is a curved shape with no straight edges or corners.
10.3. How many vertices does a cube have?
A cube has eight vertices, each formed by the intersection of three edges.
10.4. How many vertices does a tetrahedron have?
A tetrahedron has four vertices, each formed by the intersection of three edges.
10.5. What is the difference between a vertex and an edge?
A vertex is a point where edges meet, while an edge is a line segment that connects two vertices. Edges form the sides of polygons and the boundaries of faces in polyhedra.
10.6. Can a shape have an infinite number of vertices?
No, a shape cannot have an infinite number of vertices. The number of vertices is always finite, although it can be very large in complex shapes.
10.7. What is a concave vertex?
A concave vertex is a vertex where the interior angle is greater than 180 degrees. Concave vertices are also known as reflex vertices.
10.8. How is a vertex used in computer graphics?
In computer graphics, vertices are used to define the shape and appearance of three-dimensional models. Each vertex is defined by its coordinates in space, and the connections between vertices define the surface of the object.
10.9. What is Euler’s formula for vertices, edges, and faces?
Euler’s formula relates the number of vertices (V), edges (E), and faces (F) of a polyhedron: V – E + F = 2
10.10. Where can I get help if I have more questions about vertices?
If you have more questions about vertices or any other math concept, you can get help from WHAT.EDU.VN. We offer free question-answering services and connect you with experts who can provide clear and helpful explanations.
Conclusion
Understanding what a vertex is in math is crucial for grasping the fundamentals of geometry and its applications in various fields. Vertices are the cornerstones of shapes, defining their structure, properties, and characteristics. From the ancient origins of geometry to modern applications in computer graphics and engineering, vertices play a vital role in shaping our understanding of the world around us. By avoiding common mistakes and seeking help when needed, you can master the concept of vertices and excel in your mathematical studies.
Do you have any questions about vertices or other math topics? Don’t hesitate to ask at WHAT.EDU.VN, where experts are ready to provide clear and helpful answers. Our mission is to make learning accessible and enjoyable for everyone. Whether you’re a student, a professional, or simply curious about the world, we’re here to help you explore the fascinating world of mathematics. Contact us at 888 Question City Plaza, Seattle, WA 98101, United States, or via Whatsapp at +1 (206) 555-7890. You can also visit our website at what.edu.vn for more information. We look forward to helping you on your learning journey.