The Z-score, or standard score, is a crucial statistical measure that indicates how many standard deviations a data point is from its mean. Discover the definition, calculation, real-world applications, and significance of Z-scores at WHAT.EDU.VN. Delve into standard deviation, normal distribution, and statistical analysis to gain a comprehensive understanding.
1. Defining the Z-Score: A Comprehensive Overview
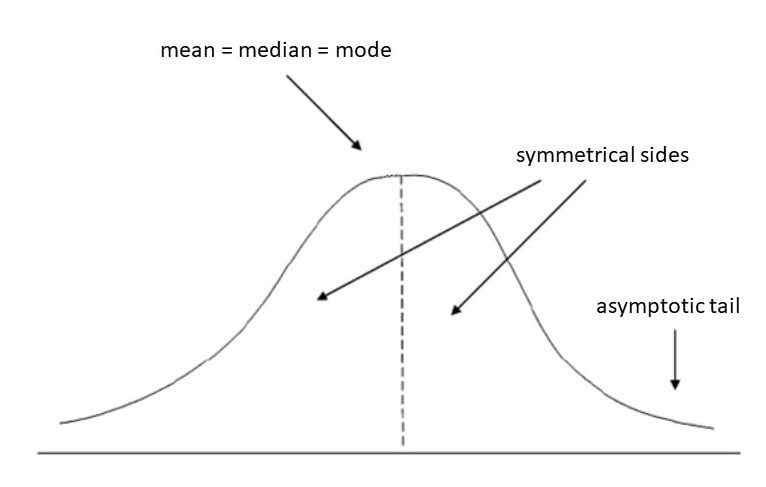
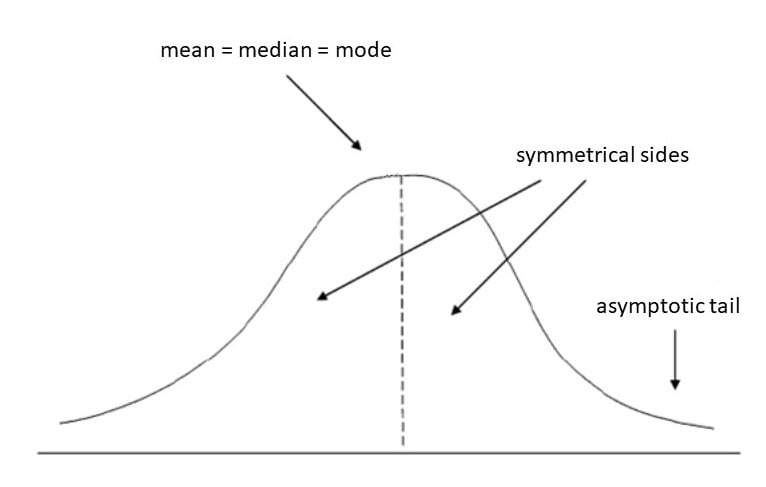
The Z-score, at its core, is a statistical measure that quantifies the divergence of a data point from the mean of a dataset. It’s expressed in terms of standard deviations, offering a standardized way to compare values from different distributions. In simpler terms, it tells you whether a particular data point is typical or atypical, relative to the rest of the data.
:max_bytes(150000):strip_icc():format(webp)/dotdash_Z-Score_Final-01-49e326d278c84f01932f418f24c39894.jpg “Z-score distribution curve illustrating standard deviations from the mean, showcasing typical and atypical data points.”)
1.1 The Formula Behind the Z-Score
The formula for calculating the Z-score is relatively straightforward:
Z = (X – μ) / σ
Where:
- Z is the Z-score
- X is the individual data point
- μ (mu) is the mean of the dataset
- σ (sigma) is the standard deviation of the dataset
This formula essentially standardizes the data, allowing for meaningful comparisons across different datasets with varying means and standard deviations.
1.2 Interpreting Z-Score Values
Understanding the Z-score value is key to unlocking its potential. Here’s a general guideline:
- Z = 0: The data point is exactly at the mean.
- Z > 0: The data point is above the mean. The higher the value, the further above the mean it is.
- Z < 0: The data point is below the mean. The lower the value (more negative), the further below the mean it is.
The magnitude of the Z-score indicates how unusual the data point is. For instance, a Z-score of 2 suggests that the data point is two standard deviations above the mean, which is considered relatively high in a normal distribution.
1.3 Z-Score vs. Standard Deviation: Clearing the Confusion
While both Z-scores and standard deviations are statistical measures, they serve distinct purposes. Standard deviation measures the spread or variability of a dataset, while the Z-score pinpoints the exact location of a data point within that distribution, relative to the mean. To illustrate, imagine two datasets:
Dataset 1: Mean = 50, Standard Deviation = 10
Dataset 2: Mean = 100, Standard Deviation = 20
A value of 60 in Dataset 1 has a Z-score of 1 ( (60-50)/10 ).
A value of 120 in Dataset 2 also has a Z-score of 1 ( (120-100)/20 ).
Although the absolute values are different, their relative positions within their respective distributions are identical.
1.4 Assumptions of the Z-Score
The Z-score relies on certain assumptions for its proper interpretation:
- Normality: The data should ideally be approximately normally distributed. While the Z-score can be calculated for non-normal data, its interpretation as a measure of “unusualness” is most accurate under normality.
- Known Mean and Standard Deviation: The mean and standard deviation of the population or sample must be known or accurately estimated.
Violations of these assumptions can affect the validity of the Z-score interpretation.
1.5 Applications of Z-Scores: A Glimpse into the Real World
Z-scores find application in a multitude of fields:
- Quality Control: Identifying defective products that deviate significantly from quality standards.
- Finance: Assessing the risk and return of investments.
- Education: Standardizing test scores for fair comparisons.
- Healthcare: Evaluating patient data relative to population norms.
- Scientific Research: Comparing results from different experiments.
1.6 Z-Table and Probability: Connecting the Dots
The Z-table, also known as the standard normal table, provides the probability of observing a value less than a given Z-score in a standard normal distribution (mean = 0, standard deviation = 1). This table is invaluable for determining the likelihood of a particular data point occurring.
For instance, a Z-score of 1.96 corresponds to a probability of approximately 0.975, meaning there’s a 97.5% chance of observing a value less than 1.96 in a standard normal distribution. This can be used to calculate p-values and perform hypothesis testing.
1.7 Limitations of the Z-Score
Despite its usefulness, the Z-score has limitations:
- Sensitivity to Outliers: Outliers can significantly influence the mean and standard deviation, thereby affecting Z-scores.
- Normality Assumption: As mentioned earlier, the interpretation of Z-scores is most accurate when data is normally distributed.
- Sample Size: Small sample sizes can lead to inaccurate estimates of the mean and standard deviation, impacting the reliability of Z-scores.
1.8 Beyond the Basics: Advanced Z-Score Applications
The Z-score concept can be extended to more complex scenarios:
- Two-Sample Z-Test: Comparing the means of two independent groups.
- Z-Score for Proportions: Analyzing proportions in a population.
- Z-Score in Regression Analysis: Assessing the significance of regression coefficients.
By understanding the fundamental principles of Z-scores, you can unlock its potential for data analysis, interpretation, and decision-making across diverse domains. Need more clarification or have specific questions? Head over to WHAT.EDU.VN and ask away – our experts are ready to provide free answers.
2. Unveiling the Z-Score Formula: A Step-by-Step Guide
The Z-score formula is the cornerstone of understanding how to standardize data. Let’s break down the formula and illustrate it with practical examples.
2.1 The Formula Revisited
As previously mentioned, the Z-score formula is:
Z = (X – μ) / σ
Where:
- Z is the Z-score
- X is the individual data point
- μ (mu) is the mean of the dataset
- σ (sigma) is the standard deviation of the dataset
2.2 Step-by-Step Calculation
To calculate a Z-score, follow these steps:
- Determine the Data Point (X): Identify the individual value you want to standardize.
- Calculate the Mean (μ): Calculate the average of all data points in the dataset.
- Calculate the Standard Deviation (σ): Determine the spread of the data around the mean.
- Apply the Formula: Plug the values of X, μ, and σ into the Z-score formula and solve for Z.
2.3 Illustrative Examples
Let’s solidify the understanding with a couple of examples:
Example 1: Exam Scores
A student scores 80 on an exam. The class average (mean) is 70, and the standard deviation is 5. Calculate the Z-score for the student’s score.
- X = 80
- μ = 70
- σ = 5
Z = (80 – 70) / 5 = 2
The student’s score is 2 standard deviations above the mean.
Example 2: Stock Returns
A stock has a return of 15% in a year. The average return for similar stocks (mean) is 10%, and the standard deviation is 8%. Calculate the Z-score for the stock’s return.
- X = 15
- μ = 10
- σ = 8
Z = (15 – 10) / 8 = 0.625
The stock’s return is 0.625 standard deviations above the mean.
2.4 Understanding the Units
The Z-score is a dimensionless number, meaning it doesn’t have any specific units. It simply represents the number of standard deviations. This allows for comparing data points from different datasets with different units.
2.5 Using Calculators and Software
While the Z-score formula is straightforward, using calculators or statistical software can expedite the process, especially when dealing with large datasets. Most spreadsheet programs (like Excel) and statistical packages (like SPSS, R) have built-in functions for calculating Z-scores.
2.6 Considerations for Grouped Data
When dealing with grouped data (data presented in intervals), you’ll need to estimate the mean and standard deviation based on the frequency distribution. This involves using the midpoint of each interval as a representative value.
2.7 Reverse Calculation: Finding X Given Z
Sometimes, you might need to find the original data point (X) given the Z-score, mean, and standard deviation. You can rearrange the Z-score formula to solve for X:
X = Z * σ + μ
2.8 Common Mistakes to Avoid
- Incorrect Mean or Standard Deviation: Ensure you’re using the correct mean and standard deviation for the specific dataset.
- Misinterpreting the Z-Score: Remember that the Z-score only indicates relative position within a distribution, not absolute value.
- Ignoring Assumptions: Be mindful of the assumptions of normality when interpreting Z-scores.
By mastering the Z-score formula and its application, you can effectively standardize data, compare values across different scales, and gain valuable insights from your data. Have a burning question about statistical calculations? Don’t hesitate – ask for free answers on WHAT.EDU.VN!
3. Z-Score in Action: Real-World Applications Across Industries
The Z-score isn’t just a theoretical concept; it’s a powerful tool used across various industries to analyze data, make informed decisions, and solve real-world problems. Let’s explore some of its practical applications.
3.1 Finance: Assessing Investment Risk and Performance
In finance, Z-scores are used to:
- Identify Unusual Stock Price Movements: A high Z-score for a stock’s daily price change might signal a potential trading opportunity or an anomaly requiring investigation.
- Compare Portfolio Performance: Standardize returns of different portfolios with varying risk profiles to assess relative performance.
- Evaluate Credit Risk: Assess the likelihood of a company defaulting on its debt obligations by analyzing financial ratios and calculating Z-scores.
Example: A portfolio manager wants to compare the performance of two portfolios. Portfolio A has a return of 12% with a standard deviation of 5%, while Portfolio B has a return of 15% with a standard deviation of 8%. The average return for the market is 10%.
- Z-score for Portfolio A: (12 – 10) / 5 = 0.4
- Z-score for Portfolio B: (15 – 10) / 8 = 0.625
Although Portfolio B has a higher return, its Z-score is only slightly higher, indicating that its higher return is partially due to its higher risk.
3.2 Healthcare: Monitoring Patient Health and Diagnosing Diseases
In healthcare, Z-scores are used to:
- Track Growth in Children: Compare a child’s height and weight to age-specific norms using Z-scores to identify potential growth abnormalities.
- Analyze Lab Results: Determine if a patient’s lab results are within the normal range by calculating Z-scores relative to population norms.
- Identify Outliers in Clinical Trials: Detect unusual responses to treatment in clinical trials.
Example: A doctor is monitoring a child’s growth. The child’s height is 2 standard deviations below the average height for their age. This could indicate a potential growth problem that needs further investigation.
3.3 Education: Standardizing Test Scores and Evaluating Student Performance
In education, Z-scores are used to:
- Standardize Test Scores: Convert scores from different tests to a common scale for fair comparisons.
- Identify Students Who Need Support: Identify students who are significantly below average in a particular subject.
- Evaluate the Effectiveness of Educational Programs: Compare the performance of students in different programs using Z-scores.
Example: A school wants to compare the performance of students on two different standardized tests. The scores on each test are converted to Z-scores, allowing for a direct comparison of student performance.
3.4 Quality Control: Identifying Defects and Ensuring Product Consistency
In manufacturing and quality control, Z-scores are used to:
- Monitor Production Processes: Track key metrics and identify deviations from expected values that could indicate problems in the production process.
- Identify Defective Products: Identify products that deviate significantly from quality standards.
Example: A factory produces light bulbs. The average lifespan of a light bulb is 1000 hours with a standard deviation of 50 hours. A light bulb that lasts only 850 hours has a Z-score of (850 – 1000) / 50 = -3. This light bulb is significantly below average and is likely defective.
3.5 Sports Analytics: Evaluating Player Performance and Team Strategies
In sports, Z-scores are used to:
- Compare Player Performance Across Different Seasons: Standardize player statistics to account for changes in the league or team.
- Identify Strengths and Weaknesses: Determine a player’s relative strengths and weaknesses compared to other players in their position.
- Evaluate Team Strategies: Assess the effectiveness of different strategies by analyzing Z-scores for key performance indicators.
Example: A baseball analyst wants to compare the performance of two players who played in different eras. The analyst converts their statistics (e.g., batting average, home runs) to Z-scores relative to their respective league averages. This allows for a more direct comparison of their performance.
3.6 Other Applications
The applications of Z-scores extend beyond these examples. They can be used in:
- Marketing: Identifying customers who are likely to respond to a marketing campaign.
- Environmental Science: Analyzing environmental data and identifying pollution hotspots.
- Social Sciences: Comparing survey responses across different groups.
The Z-score is a versatile tool that can be applied in any situation where you need to standardize data, compare values across different scales, and identify outliers. Do you have a real-world problem that could be solved with statistical analysis? Ask your question on WHAT.EDU.VN and get expert advice for free!
4. What Constitutes a “Good” Z-Score? Interpretation and Context
The concept of a “good” Z-score is highly dependent on the context of the analysis and the specific goals of the user. There isn’t a universal threshold that defines a Z-score as inherently good or bad. Instead, the interpretation should be based on the specific application and the characteristics of the data.
4.1 Understanding the Normal Distribution
To interpret Z-scores effectively, it’s crucial to understand the properties of the normal distribution. In a standard normal distribution:
- Approximately 68% of the data falls within 1 standard deviation of the mean (Z-score between -1 and 1).
- Approximately 95% of the data falls within 2 standard deviations of the mean (Z-score between -2 and 2).
- Approximately 99.7% of the data falls within 3 standard deviations of the mean (Z-score between -3 and 3).
This means that Z-scores outside the range of -2 to 2 are considered relatively unusual, and Z-scores outside the range of -3 to 3 are considered very rare.
4.2 Context Matters: Application-Specific Interpretation
The interpretation of a “good” Z-score varies depending on the application:
- Quality Control: In quality control, a Z-score close to 0 might be considered ideal, as it indicates that the product is close to the target specification. However, the acceptable range depends on the specific product and the tolerance limits.
- Finance: In finance, a high positive Z-score for a stock’s return might be considered good, as it indicates that the stock is outperforming its peers. However, it’s important to consider the risk associated with the stock.
- Healthcare: In healthcare, a Z-score outside the normal range might indicate a potential health problem. However, the specific interpretation depends on the lab test and the patient’s medical history.
- Education: In education, a high Z-score on a standardized test might be considered good, as it indicates that the student is performing well. However, it’s important to consider the student’s overall academic performance and other factors.
4.3 Identifying Outliers
Z-scores are often used to identify outliers in a dataset. A common rule of thumb is to consider data points with Z-scores greater than 3 or less than -3 as outliers. However, this threshold can be adjusted depending on the specific dataset and the goals of the analysis.
4.4 Considering the Sample Size
The interpretation of Z-scores should also take into account the sample size. In small samples, extreme Z-scores are more likely to occur due to random chance. Therefore, a more conservative threshold might be used to identify outliers.
4.5 Beyond Thresholds: Understanding the Distribution
Instead of relying solely on fixed thresholds, it’s important to understand the overall distribution of the data. Visualizing the data with histograms or box plots can help identify potential outliers and assess the normality of the distribution.
4.6 Examples
Here are a few examples to illustrate how the interpretation of a “good” Z-score depends on the context:
- Example 1: Manufacturing A manufacturing company wants to ensure that the diameter of a metal rod is close to the target of 10 mm. They calculate the Z-scores for a sample of rods. A Z-score close to 0 is considered good, as it indicates that the rod is close to the target diameter.
- Example 2: Investing An investor is evaluating two different stocks. Stock A has a Z-score of 2 for its annual return, while Stock B has a Z-score of 1.5. Stock A is considered to have a better return relative to its risk.
- Example 3: Healthcare A doctor is reviewing a patient’s lab results. The patient’s cholesterol level has a Z-score of 3.5, which is considered high and indicates a potential health risk.
The concept of a “good” Z-score is subjective and depends on the specific context. Understanding the normal distribution, considering the application, identifying outliers, and taking into account the sample size are all important factors in interpreting Z-scores effectively. Still unsure about interpreting your specific Z-score? Get free personalized guidance on WHAT.EDU.VN – ask your question today!
5. The Significance of Z-Scores: Unveiling its Importance in Statistical Analysis
Z-scores play a vital role in statistical analysis by providing a standardized way to understand and compare data points within a distribution. Their significance stems from their ability to:
5.1 Standardize Data for Comparison
One of the most important functions of Z-scores is to standardize data from different distributions. This allows for meaningful comparisons even when the data is measured on different scales or has different units.
Example: Comparing exam scores from two different classes with different grading scales. By converting the scores to Z-scores, you can compare a student’s performance relative to their classmates, regardless of the grading scale used in each class.
5.2 Identify Relative Position Within a Distribution
Z-scores indicate the relative position of a data point within a distribution, telling you how far above or below the mean it lies in terms of standard deviations. This provides valuable insights into the unusualness or typicality of the data point.
Example: A Z-score of 2 indicates that the data point is 2 standard deviations above the mean, which is relatively high and suggests that it’s an unusual value.
5.3 Facilitate Hypothesis Testing
Z-scores are used in hypothesis testing to determine the statistical significance of a result. By calculating a Z-score for a sample mean, you can determine the probability of observing such a mean if the null hypothesis is true. This allows you to make informed decisions about whether to reject or fail to reject the null hypothesis.
Example: A researcher wants to test whether a new drug is effective in lowering blood pressure. They calculate the Z-score for the difference in blood pressure between the treatment group and the control group. If the Z-score is large enough, they can reject the null hypothesis and conclude that the drug is effective.
5.4 Detect Outliers and Anomalies
Z-scores are a powerful tool for identifying outliers and anomalies in a dataset. Data points with extreme Z-scores are likely to be outliers, which may represent errors in the data or unusual events that warrant further investigation.
Example: In a manufacturing process, a Z-score of -4 for a product’s weight might indicate a malfunction in the equipment.
5.5 Enable Comparisons to the Standard Normal Distribution
The Z-score transforms any normal distribution into the standard normal distribution (mean = 0, standard deviation = 1). This allows you to use the standard normal table to find probabilities associated with different Z-scores.
Example: You can use the standard normal table to find the probability of observing a Z-score greater than 1.96, which is approximately 0.025.
5.6 Improve Data Interpretation
By standardizing data and providing a measure of relative position, Z-scores can significantly improve data interpretation. They help to put data into perspective and make it easier to draw meaningful conclusions.
Example: Instead of simply knowing that a student scored 85 on a test, a Z-score of 1.5 tells you that the student performed well above average compared to their peers.
5.7 Support Decision-Making
Z-scores provide valuable information for decision-making in a wide range of fields. They help to identify risks, opportunities, and areas that require further attention.
Example: A financial analyst might use Z-scores to identify undervalued stocks or assess the creditworthiness of a borrower.
5.8 Limitations
While Z-scores are a valuable statistical tool, it’s important to be aware of their limitations:
- Normality Assumption: Z-scores are most effective when the data is approximately normally distributed.
- Sensitivity to Outliers: Outliers can significantly influence the mean and standard deviation, thereby affecting Z-scores.
Despite these limitations, Z-scores remain a fundamental concept in statistical analysis, providing a powerful way to standardize data, compare values, and make informed decisions. Still wondering how Z-scores can help you with your specific data analysis? Get free expert answers on WHAT.EDU.VN!
6. Navigating Z-Scores and Standard Deviation: Key Differences and Relationships
While Z-scores and standard deviation are both statistical measures related to the distribution of data, they represent different aspects and serve different purposes. Understanding their key differences and relationships is crucial for effective data analysis.
6.1 Standard Deviation: Measuring Variability
Standard deviation measures the spread or dispersion of data points around the mean of a distribution. A high standard deviation indicates that the data points are widely scattered, while a low standard deviation indicates that they are clustered closely around the mean.
Formula:
The standard deviation (σ) is calculated as the square root of the variance:
σ = √[ Σ(Xi – μ)² / (N – 1) ] (for a sample)
Where:
- Xi is each individual data point
- μ is the mean of the dataset
- N is the number of data points
6.2 Z-Score: Measuring Relative Position
The Z-score, on the other hand, measures the number of standard deviations a particular data point is away from the mean. It standardizes the data and allows you to compare values from different distributions.
Formula:
Z = (X – μ) / σ
Where:
- Z is the Z-score
- X is the individual data point
- μ is the mean of the dataset
- σ is the standard deviation of the dataset
6.3 Key Differences
Here’s a table summarizing the key differences between Z-scores and standard deviation:
| Feature | Standard Deviation | Z-Score |
|---|---|---|
| Purpose | Measures the spread or variability of data | Measures the relative position of a data point |
| Units | Same units as the original data | Dimensionless (number of standard deviations) |
| Value | Always non-negative | Can be positive, negative, or zero |
| Interpretation | Higher value indicates greater variability | Indicates how far above or below the mean a point is |
| Distribution | Describes the overall spread of the entire dataset | Applies to individual data points within the dataset |




6.4 The Relationship: Z-Score Depends on Standard Deviation
The Z-score is directly dependent on the standard deviation. You cannot calculate a Z-score without knowing the standard deviation of the dataset. The Z-score uses the standard deviation as a yardstick to measure the distance of a data point from the mean.
6.5 Illustrative Example
Let’s say you have the following dataset: 10, 12, 15, 18, 20
- Calculate the Mean: μ = (10 + 12 + 15 + 18 + 20) / 5 = 15
- Calculate the Standard Deviation: σ ≈ 3.87
- Calculate the Z-Score for the data point 12: Z = (12 – 15) / 3.87 ≈ -0.77
The standard deviation tells you that the data points are, on average, about 3.87 units away from the mean. The Z-score of -0.77 tells you that the data point 12 is 0.77 standard deviations below the mean.
6.6 When to Use Each Measure
- Use Standard Deviation: When you want to understand the overall spread or variability of a dataset.
- Use Z-Score: When you want to compare individual data points to the rest of the distribution, especially when comparing data from different distributions.
6.7 Common Misconceptions
- Confusing Standard Deviation with Variance: Standard deviation is the square root of the variance. Variance is another measure of spread, but standard deviation is easier to interpret because it’s in the same units as the original data.
- Thinking Z-Score Represents Absolute Value: Z-score only represents relative position within a distribution, not absolute value or magnitude.
Understanding the nuances between Z-scores and standard deviation empowers you to analyze data with greater precision and draw more meaningful conclusions. Still unsure how to choose the right statistical measure for your analysis? Ask your data-related questions for free on WHAT.EDU.VN!
7. Frequently Asked Questions (FAQ) About Z-Scores
Here’s a compilation of frequently asked questions about Z-scores, covering various aspects of their application and interpretation:
| Question | Answer |
|---|---|
| What is the purpose of a Z-score? | A Z-score standardizes data, allowing you to compare values from different distributions. It indicates how many standard deviations a data point is away from the mean. |
| How do I interpret a negative Z-score? | A negative Z-score indicates that the data point is below the mean. The more negative the Z-score, the further below the mean it is. |
| Is a high Z-score always good? | Not necessarily. The interpretation depends on the context. In some cases, a high Z-score might be desirable (e.g., high stock return), while in others, it might indicate a problem (e.g., high cholesterol level). |
| What is a typical range for Z-scores? | In a normal distribution, approximately 68% of the data falls within a Z-score of -1 to 1, 95% within -2 to 2, and 99.7% within -3 to 3. |
| How do Z-scores help identify outliers? | Data points with Z-scores greater than 3 or less than -3 are often considered outliers. However, this threshold can be adjusted depending on the dataset and the goals of the analysis. |
| What if my data is not normally distributed? | While Z-scores can still be calculated, their interpretation as a measure of “unusualness” is less accurate. Consider using other statistical methods that are more appropriate for non-normal data. |
| Can I use Z-scores with small sample sizes? | Yes, but be cautious. Small sample sizes can lead to inaccurate estimates of the mean and standard deviation, which can affect the reliability of Z-scores. |
| How are Z-scores used in hypothesis testing? | Z-scores are used to calculate p-values, which are used to determine the statistical significance of a result. A small p-value indicates strong evidence against the null hypothesis. |
| What is the difference between a Z-score and a t-score? | Z-scores are used when the population standard deviation is known, while t-scores are used when the population standard deviation is unknown and estimated from the sample. T-scores are also more appropriate for small sample sizes. |
| Where can I learn more about Z-scores? | You can find more information about Z-scores in statistics textbooks, online resources, and statistical software documentation. You can also ask questions on WHAT.EDU.VN for free! |
This FAQ provides a quick reference for common questions about Z-scores. If you have a question that’s not answered here, don’t hesitate to ask on WHAT.EDU.VN – our community of experts is ready to help.
8. Conclusion: Mastering the Z-Score for Data-Driven Insights
The Z-score is a fundamental statistical tool with widespread applications across various industries. By understanding its definition, calculation, interpretation, and limitations, you can unlock its potential for data analysis, decision-making, and problem-solving. From standardizing data to identifying outliers, the Z-score provides valuable insights into the relative position of data points within a distribution.
Mastering the Z-score empowers you to:
- Compare Data Effectively: Standardize data from different sources for meaningful comparisons.
- Identify Unusual Events: Detect outliers and anomalies that warrant further investigation.
- Make Informed Decisions: Support decision-making with data-driven insights.
- Communicate Results Clearly: Present data in a standardized and easily understandable format.
As you continue your journey in data analysis and statistics, remember that the Z-score is just one tool in your toolbox. Combine it with other statistical methods and domain expertise to gain a comprehensive understanding of your data.
Do you have more questions about Z-scores or other statistical concepts? Are you struggling to apply Z-scores to your specific data analysis problems? Don’t hesitate to seek help from the experts at WHAT.EDU.VN. We offer a free platform where you can ask any question and receive prompt, accurate answers from a community of knowledgeable professionals.
Unlock the power of data with WHAT.EDU.VN. Get your questions answered for free!
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: WHAT.EDU.VN
Don’t let your data questions go unanswered. Visit what.edu.vn today and start exploring the world of data-driven insights!