What Is An Equilateral Triangle? This fundamental geometric shape, explored in detail by WHAT.EDU.VN, is more than just a three-sided figure. It’s a gateway to understanding mathematical concepts and real-world applications. Delve into the characteristics, formulas, and fascinating properties of this equiangular triangle, and discover how it forms the building blocks of complex structures. Let WHAT.EDU.VN be your guide to mastering geometric principles. Are you looking for assistance with a tricky math problem? Submit your questions to WHAT.EDU.VN and receive expert answers for free.
1. Understanding the Equilateral Triangle Definition
An equilateral triangle is defined as a triangle where all three sides are of equal length. This fundamental characteristic leads to another crucial property: all three interior angles are also equal, each measuring 60 degrees. This equiangular nature makes it a uniquely symmetrical and balanced geometric figure. Essentially, it’s a regular polygon with three sides, showcasing perfect harmony between its sides and angles.
2. The Shape and Symmetry of Equilateral Triangles
The term “equilateral” itself breaks down to “equi” (equal) and “lateral” (sides), clearly indicating its defining feature. This equality extends beyond just the sides, influencing its overall shape and symmetry. Unlike scalene triangles, where all sides have different lengths, or isosceles triangles with only two equal sides, equilateral triangles exhibit perfect symmetry around their center. This symmetry contributes to their prevalence in various fields, from art and design to engineering and architecture. The consistent shape of an equilateral triangle makes it a predictable and reliable element in any construction or design.
3. Key Properties of Equilateral Triangles Explained
Equilateral triangles possess several distinctive properties that set them apart:
- Equal Sides: All three sides are congruent (equal in length).
- Equal Angles: All three interior angles are congruent and measure 60 degrees each.
- Regular Polygon: It is a regular polygon, meaning all its sides and angles are equal.
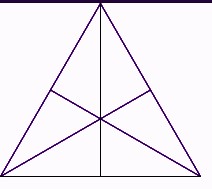
- Angle Bisector Property: A perpendicular line drawn from any vertex to the opposite side bisects both the side and the vertex angle, creating two 30-degree angles.
- Coincident Centers: The orthocenter (intersection of altitudes), centroid (intersection of medians), incenter (center of inscribed circle), and circumcenter (center of circumscribed circle) all coincide at the same point.
- Median, Angle Bisector, and Altitude: The median, angle bisector, and altitude for each side are all the same line segment.
- Area: The area is calculated using the formula √3a²/4, where ‘a’ is the side length.
- Perimeter: The perimeter is simply 3a, where ‘a’ is the side length.
- Height: The height (altitude) is calculated as √3a/2, where ‘a’ is the side length.
These properties make equilateral triangles incredibly useful in various mathematical and practical applications.
4. Comparing Equilateral, Isosceles, and Scalene Triangles
| Feature | Equilateral Triangle | Isosceles Triangle | Scalene Triangle |
|---|---|---|---|
| Side Lengths | All three sides are equal. | At least two sides are equal. | All three sides are unequal. |
| Interior Angles | All three angles are equal (60 degrees). | Two angles are equal (opposite equal sides). | All three angles are unequal. |
| Symmetry | High symmetry; 3 lines of reflection. | One line of reflection. | No lines of reflection. |
| Regularity | Regular polygon. | Irregular polygon. | Irregular polygon. |
| Altitude/Median/Bisector | Coincide for each side. | Coincide only for the base (unequal side). | Do not coincide. |
| Examples | Many geometric designs, tessellations. | Roof trusses, some architectural elements. | Irregular shapes in nature, freeform designs. |

Understanding these differences helps in identifying and classifying triangles based on their properties.
5. The Equilateral Triangle Theorem: A Deeper Dive
The Equilateral Triangle Theorem provides a unique relationship within a circumcircle. If ABC is an equilateral triangle and P is a point on the arc BC of the circumcircle of triangle ABC, then the theorem states:
PA = PB + PC
This theorem highlights the interconnectedness of geometry and circle properties.
Proof:
For a cyclic quadrilateral ABPC:
PA⋅BC = PB⋅AC + PC⋅AB
Since ABC is an equilateral triangle:
AB = BC = AC
Therefore:
PA.AB = PB.AB + PC.AB
Taking AB as a common factor:
PA.AB = AB(PB + PC)
PA = PB + PC
This proof demonstrates how the equal sides of an equilateral triangle influence relationships within a circle that circumscribes it.
6. Mastering Equilateral Triangle Formulas: Area, Perimeter, and Height
Understanding the formulas for area, perimeter, and height is essential for working with equilateral triangles.
6.1. Unlocking the Area of an Equilateral Triangle
The area of an equilateral triangle represents the two-dimensional space it occupies. The formula is:
A = √3a²/4
Where ‘a’ represents the length of a side.
Derivation:
The area of any triangle is given by:
Area = ½ x base x height
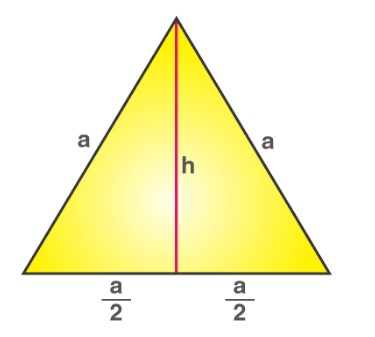
In an equilateral triangle, the base is ‘a’, and the height needs to be determined. The altitude bisects the base, creating two right-angled triangles. Using the Pythagorean theorem:
a² = h² + (a/2)²
h² = a² – (a²/4)
h² = 3a²/4
h = √3a/2
Substituting the value of h in the area formula:
Area = ½ x a x (√3a/2)
Area = √3a²/4
This formula allows you to quickly calculate the area of any equilateral triangle if you know the side length.
6.2. Calculating the Perimeter of an Equilateral Triangle
The perimeter is the total distance around the triangle. For an equilateral triangle, it’s simply the sum of its three equal sides:
P = 3a
Where ‘a’ is the length of one side. This is perhaps the easiest formula to remember and apply.
6.3. Finding the Height of an Equilateral Triangle
The height (or altitude) is the perpendicular distance from a vertex to the opposite side. As derived in the area section, the formula is:
h = √3a/2
Where ‘a’ is the length of a side. This formula is crucial for various calculations and constructions involving equilateral triangles.
6.4. Equilateral Triangle Formula Summary
| Property | Formula | Description |
|---|---|---|
| Area | √3a²/4 | Space occupied by the triangle. |
| Perimeter | 3a | Total distance around the triangle. |
| Height | √3a/2 | Perpendicular distance from vertex to base. |
Understanding these formulas unlocks your ability to analyze and manipulate equilateral triangles in geometric problems.
7. The Centroid of an Equilateral Triangle: Finding the Balance Point
The centroid is the geometric center of the triangle, the point where the three medians intersect. A median is a line segment from a vertex to the midpoint of the opposite side. In an equilateral triangle, the centroid coincides with the incenter, circumcenter, and orthocenter, simplifying its location.
The centroid is equidistant from all three vertices and all three sides, making it the triangle’s “balancing point.” If you were to cut out an equilateral triangle from a piece of cardboard, you could balance it perfectly on a pin placed at the centroid. This property makes it important in engineering and design applications where balance and stability are crucial.
8. Understanding the Circumcenter of an Equilateral Triangle
The circumcenter is the center of the circle that passes through all three vertices of the triangle (the circumcircle). It is found by locating the intersection point of the perpendicular bisectors of the sides. In an equilateral triangle, the circumcenter coincides with the centroid, incenter, and orthocenter due to its high degree of symmetry. This means that the center of the circumcircle is also the balancing point of the triangle and the center of its inscribed circle.
This unique property of equilateral triangles simplifies geometric constructions and calculations related to circles and triangles.
9. Practical Examples of Equilateral Triangle Calculations
Let’s solidify your understanding with some solved examples:
Q.1: Find the area of an equilateral triangle ABC, where AB = AC = BC = 4cm.
Solution:
Using the formula:
Area = √3a²/4
Given a = 4cm
Area = √3(4)²/4
Area = 4√3 cm²
Q.2: Find the altitude of an equilateral triangle whose sides are equal to 10cm.
Solution:
Using the formula:
Height = √3a/2
Since, a = 10cm
Height = √3 x (10/2)
Height = 5√3 cm
These examples demonstrate how to apply the formulas in real-world scenarios.
10. Real-World Applications of Equilateral Triangles
Equilateral triangles aren’t just theoretical concepts; they appear in numerous real-world applications:
- Architecture: Used in structural designs for stability and strength, such as trusses and geodesic domes.
- Engineering: Employed in bridge construction, especially in triangular support structures.
- Design: Found in logos, patterns, and decorative elements, prized for their visual appeal and balance.
- Nature: Observed in natural formations like crystal structures and honeycombs.
- Games and Puzzles: A fundamental shape in games, puzzles, and geometric art.
- Navigation: Used in certain navigational tools and map-making techniques.
Their inherent stability, symmetry, and predictable geometry make them a versatile shape in many fields.
11. Frequently Asked Questions About Equilateral Triangles
Here are some common questions and answers about equilateral triangles:
| Question | Answer |
|---|---|
| What is an equilateral triangle? | A triangle with all three sides equal in length and all three angles equal to 60 degrees. |
| What is the area formula? | A = (√3/4)a², where ‘a’ is the side length. |
| What is the perimeter formula? | P = 3a, where ‘a’ is the side length. |
| What is the height formula? | h = (√3/2)a, where ‘a’ is the side length. |
| Is it a regular polygon? | Yes, it is a regular polygon because all sides and angles are equal. |
| How many sides does it have? | 3 |
| What are other types of triangles based on sides? | Scalene (no equal sides), Isosceles (at least two equal sides). |
| What is the perimeter if the side is 10cm? | Perimeter = 3 x 10cm = 30cm |
| Where do the centroid and circumcenter lie? | In an equilateral triangle, the centroid, incenter, circumcenter, and orthocenter all coincide at the same point, at the center of the triangle. |
| How is it used in architecture? | Due to its inherent strength and stability, equilateral triangles are used in structural designs such as trusses, bridges, and geodesic domes to evenly distribute weight and resist external forces effectively. |
12. Explore Geometry Further with WHAT.EDU.VN
Do you still have questions about equilateral triangles or other geometric concepts? WHAT.EDU.VN offers a platform to ask any question and receive answers from experts, free of charge. Whether you’re struggling with homework, curious about a specific topic, or simply seeking to expand your knowledge, WHAT.EDU.VN is here to help.
13. Unlock Free Answers to All Your Questions on WHAT.EDU.VN
Navigating complex concepts can be challenging. WHAT.EDU.VN simplifies the process by providing a space where you can freely ask questions and receive clear, concise answers from knowledgeable individuals. Our platform is designed to make learning accessible and enjoyable for everyone.
14. Need Homework Help? WHAT.EDU.VN is Your Solution!
Stuck on a tough assignment? WHAT.EDU.VN offers a supportive community where you can seek assistance with homework questions across various subjects. Don’t struggle alone – submit your questions and get the guidance you need to succeed.
15. Get Expert Answers Without Spending a Dime on WHAT.EDU.VN
Accessing quality education shouldn’t break the bank. WHAT.EDU.VN is committed to providing free answers to your questions, ensuring that everyone has the opportunity to learn and grow.
Ready to explore the world of knowledge? Visit WHAT.EDU.VN today!
Address: 888 Question City Plaza, Seattle, WA 98101, United States
Whatsapp: +1 (206) 555-7890
Website: WHAT.EDU.VN
Don’t hesitate to ask your questions and unlock a world of free knowledge! what.edu.vn is ready to help you learn and grow.