What Is an Even Function? Definition and Examples

What Is An Even Function? This is a common question, and at WHAT.EDU.VN, we provide clear answers. Understanding even functions is crucial in mathematics, especially in calculus and analysis. We offer comprehensive explanations and examples. Learn about function symmetry, properties of functions, and function behavior right here.

1. Understanding Even Functions: The Basics

What exactly defines an even function? Let’s delve into the foundational concepts:

1.1. Formal Definition of an Even Function

A function f(x) is considered an even function if it satisfies a specific condition:

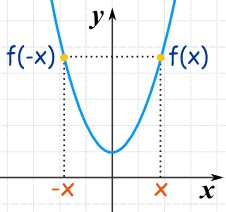
f(x) = f(-x) for all x in the domain of the function.

This means that if you input x into the function, you get the same result as if you input -x. The sign of the input doesn’t affect the output.

1.2. Graphical Interpretation: Symmetry About the Y-Axis

Even functions exhibit a distinct graphical property: their graphs are symmetric with respect to the y-axis. This symmetry implies that if you were to fold the graph along the y-axis, the two halves would perfectly overlap.

1.3. Examples of Even Functions

To solidify the concept, let’s look at some common examples:

• f(x) = x²: This is the classic example of an even function. Squaring a number always results in a positive value, regardless of whether the original number was positive or negative.
• f(x) = cos(x): The cosine function is also even. The cosine of an angle is the same as the cosine of its negative angle.
• f(x) = |x|: The absolute value function is even. Taking the absolute value of a number makes it positive, irrespective of its original sign.
• f(x) = x⁴ + 3x² + 5: Polynomials with only even powers of x are even functions.
• f(x) = c: Any constant function is even.

1.4. Why is Identifying Even Functions Important?

Recognizing even functions simplifies mathematical analyses in several ways:

• Integration: The integral of an even function over a symmetric interval [-a, a] is twice the integral over the interval [0, a]. This property reduces computation.
• Series Expansions: Even functions have specific forms of series expansions, such as the Fourier cosine series, which simplifies complex representations.
• Symmetry Analysis: Understanding symmetry properties helps in physics, engineering, and computer graphics, where even functions model symmetrical phenomena.

2. Proving a Function is Even: Step-by-Step Guide

How do you mathematically prove that a function is even? Here’s a systematic approach:

2.1. Steps to Prove a Function is Even

1. Start with the function: Begin with the function you want to prove is even, f(x).
2. Substitute -x: Replace every instance of x in the function with -x, resulting in f(-x).
3. Simplify: Simplify the expression f(-x) as much as possible. Use algebraic manipulations and trigonometric identities if needed.
4. Compare: Check if the simplified f(-x) is equal to the original function f(x).
5. Conclusion: If f(-x) = f(x), then the function is even. If not, the function is not even.

2.2. Example Proof: f(x) = x² + cos(x)

Let’s prove that f(x) = x² + cos(x) is an even function.

1. Function: f(x) = x² + cos(x)
2. Substitute -x: f(-x) = (-x)² + cos(-x)
3. Simplify:
   • (-x)² = x²
   • cos(-x) = cos(x) (since cosine is an even function)
   • So, f(-x) = x² + cos(x)
4. Compare: f(-x) = x² + cos(x) = f(x)
5. Conclusion: Since f(-x) = f(x), the function f(x) = x² + cos(x) is even.

2.3. Common Mistakes to Avoid

• Incorrect Simplification: Ensure all algebraic and trigonometric simplifications are correct.
• Misunderstanding the Definition: Always adhere to the definition f(-x) = f(x).
• Assuming without Proof: Don’t assume a function is even based on appearance. Always perform the algebraic proof.

3. Properties and Theorems Related to Even Functions

Even functions possess unique properties that simplify mathematical operations and analyses.

3.1. Symmetry Properties in Calculus

• Integration: If f(x) is an even function, then:

  ∫_-a^a f(x) dx = 2 ∫₀^a f(x) dx

  This property states that the integral from -a to a is twice the integral from 0 to a, due to the symmetry.

• Differentiation: The derivative of an even function is always an odd function. If f(x) is even, then f'(x) is odd.

3.2. Combining Even Functions

• Addition/Subtraction:
  • The sum of two even functions is even. If f(x) and g(x) are even, then f(x) + g(x) is even.
  • The difference of two even functions is even. If f(x) and g(x) are even, then f(x) – g(x) is even.
• Multiplication/Division:
  • The product of two even functions is even. If f(x) and g(x) are even, then f(x) g(x)* is even.
  • The quotient of two even functions is even. If f(x) and g(x) are even, then f(x) / g(x) is even.
• Composition: The composition of two even functions is even. If f(x) and g(x) are even, then f(g(x)) is even.

3.3. Practical Applications of these Properties

• Signal Processing: Even functions are used in signal processing to analyze symmetrical signals, simplifying computations.
• Physics: In quantum mechanics, parity (evenness or oddness of a wave function) simplifies calculations related to particle behavior.
• Engineering: Engineers use properties of even functions to design systems with symmetrical responses, ensuring balanced performance.

4. Identifying Non-Even Functions: Odd and Neither

Not all functions are even. Some are odd, and some are neither even nor odd. Understanding these categories is essential.

4.1. Definition of an Odd Function

A function f(x) is odd if it satisfies:

• f(-x) = -f(x) for all x in the domain.

This means that if you input -x, the result is the negative of what you would get by inputting x.

4.2. Graphical Interpretation: Symmetry About the Origin

Odd functions are symmetric about the origin. If you rotate the graph 180 degrees around the origin, it remains unchanged.

4.3. Examples of Odd Functions

• f(x) = x: The simplest odd function.
• f(x) = sin(x): The sine function is odd.
• f(x) = x³: Cubing a number preserves its sign, making it odd.
• f(x) = x⁵ – 2x³ + x: Polynomials with only odd powers of x are odd functions.

4.4. Functions that are Neither Even Nor Odd

Functions that do not satisfy the conditions for either even or odd functions are classified as neither. Examples include:

• f(x) = x² + x: This function has both even and odd terms.
• f(x) = e^x: The exponential function is neither even nor odd.
• f(x) = x + 1: A simple linear function that is neither even nor odd.

4.5. How to Determine if a Function is Even, Odd, or Neither

1. Evaluate f(-x): Substitute -x into the function.
2. Simplify: Simplify the expression.
3. Compare:
   • If f(-x) = f(x), the function is even.
   • If f(-x) = -f(x), the function is odd.
   • If neither condition is met, the function is neither even nor odd.

5. Advanced Concepts: Even Functions in Fourier Analysis

Even functions play a significant role in Fourier analysis, a powerful tool in mathematics and engineering.

5.1. Fourier Series of Even Functions

The Fourier series of an even function contains only cosine terms. The sine terms are zero due to the symmetry. This simplifies the Fourier series representation significantly. The Fourier series of an even function f(x) on the interval [-L, L] is:

f(x) = a₀/2 + Σ_n=1^∞ a_n cos(nπx/L)

Where:

• a₀ = (2/L) ∫₀^L f(x) dx
• a_n = (2/L) ∫₀^L f(x) cos(nπx/L) dx

5.2. Practical Examples in Signal Processing

In signal processing, even functions represent signals that are symmetrical in time. The Fourier series of these signals contains only cosine components, simplifying analysis and filtering. For instance, a square wave that is symmetrical about the y-axis is an even function, and its Fourier series consists of cosine terms.

5.3. Relationship with Fourier Transforms

The Fourier transform of an even function is real and even. This means that the transform has no imaginary part and is symmetric about the frequency axis. This property is used in image processing and communications to analyze and process symmetrical data.

5.4. Advantages of Using Even Functions in Analysis

• Simplification: Even functions simplify Fourier analysis by eliminating sine terms.
• Efficiency: Computations are more efficient because only cosine coefficients need to be calculated.
• Interpretation: The resulting Fourier series is easier to interpret due to its symmetry.

6. Real-World Applications of Even Functions

Even functions are not just abstract mathematical concepts; they have practical applications in various fields.

6.1. Physics: Harmonic Oscillators

In physics, the potential energy of a harmonic oscillator is an even function. The potential energy V(x) is proportional to x², which is even. This symmetry simplifies the analysis of the oscillator’s motion and energy levels.

6.2. Engineering: Circuit Design

In electrical engineering, symmetrical circuits often exhibit even function characteristics. The response of a circuit to a symmetrical input can be described using even functions, simplifying the design and analysis of filters and amplifiers.

6.3. Computer Graphics: Image Processing

In computer graphics, even functions are used in image processing to create symmetrical effects. Convolution filters that are even functions preserve symmetry in images, which is useful for tasks like blurring and sharpening.

6.4. Economics: Utility Functions

In economics, some utility functions are even, reflecting symmetrical preferences. For example, a utility function that depends on the square of consumption deviations from a target level is an even function, indicating that deviations above or below the target are equally undesirable.

6.5. Statistics: Probability Distributions

In statistics, the probability density function of a normal distribution is an even function. This symmetry simplifies calculations related to probabilities and expected values.

7. Common Questions and Misconceptions About Even Functions

Let’s address some frequently asked questions and clear up common misconceptions about even functions.

7.1. Is the Zero Function Always Even?

Yes, the zero function, f(x) = 0, is always even. This is because f(-x) = 0 = f(x) for all x.

7.2. Can a Function Be Both Even and Odd?

Yes, but only the zero function, f(x) = 0, can be both even and odd. This is because for a function to be both even and odd, it must satisfy both f(-x) = f(x) and f(-x) = -f(x), which implies f(x) = -f(x), and hence f(x) = 0.

7.3. Is a Constant Function Always Even?

Yes, any constant function f(x) = c is even. This is because f(-x) = c = f(x).

7.4. What Happens When You Multiply an Even Function by an Odd Function?

The result is an odd function. If f(x) is even and g(x) is odd, then h(x) = f(x) g(x) is odd. This is because h(-x) = f(-x) g(-x) = f(x) -g(x) = -h(x)*.

7.5. How Do Even Functions Simplify Integration?

Even functions simplify integration over symmetric intervals because the integral from -a to a is twice the integral from 0 to a:

∫_-a^a f(x) dx = 2 ∫₀^a f(x) dx

This reduces the computational effort by half.

8. Practice Problems: Test Your Understanding

To reinforce your understanding of even functions, try these practice problems.

8.1. Problem 1: Determine if f(x) = x⁴ – 2x² + 1 is Even, Odd, or Neither

1. Evaluate f(-x): f(-x) = (-x)⁴ – 2(-x)² + 1
2. Simplify: f(-x) = x⁴ – 2x² + 1
3. Compare: f(-x) = f(x)

Conclusion: The function is even.

8.2. Problem 2: Determine if f(x) = x³ + sin(x) is Even, Odd, or Neither

1. Evaluate f(-x): f(-x) = (-x)³ + sin(-x)
2. Simplify: f(-x) = -x³ – sin(x) = -(x³ + sin(x))
3. Compare: f(-x) = -f(x)

Conclusion: The function is odd.

8.3. Problem 3: Determine if f(x) = x² + x is Even, Odd, or Neither

1. Evaluate f(-x): f(-x) = (-x)² + (-x)
2. Simplify: f(-x) = x² – x
3. Compare: f(-x) ≠ f(x) and f(-x) ≠ -f(x)

Conclusion: The function is neither even nor odd.

8.4. Problem 4: Determine if f(x) = cos(x) + 2 is Even, Odd, or Neither

1. Evaluate f(-x): f(-x) = cos(-x) + 2
2. Simplify: f(-x) = cos(x) + 2
3. Compare: f(-x) = f(x)

Conclusion: The function is even.

8.5. Problem 5: Determine if f(x) = e^x2 is Even, Odd, or Neither

1. Evaluate f(-x): f(-x) = e^(-x)2
2. Simplify: f(-x) = e^x2
3. Compare: f(-x) = f(x)

Conclusion: The function is even.

9. Resources for Further Learning

To deepen your understanding of even functions and related topics, explore these resources.

9.1. Textbooks on Calculus and Analysis

• “Calculus” by James Stewart
• “Calculus” by Thomas Finney
• “Real Analysis” by Royden and Fitzpatrick

9.2. Online Courses and Tutorials

• Khan Academy: Calculus
• MIT OpenCourseWare: Single Variable Calculus
• Coursera: Mathematics for Machine Learning

9.3. Websites with Mathematical Resources

• MathWorld
• Wolfram Alpha
• WHAT.EDU.VN

9.4. Software Tools for Graphing and Analysis

• Desmos
• GeoGebra
• MATLAB

10. Conclusion: Mastering Even Functions

Understanding even functions is a fundamental aspect of mathematics. From their symmetrical properties to their applications in Fourier analysis and real-world scenarios, even functions play a crucial role in simplifying complex problems. By mastering the concepts and techniques discussed in this comprehensive guide, you can enhance your mathematical toolkit and tackle a wide range of challenges.

Do you have any questions or need further clarification? At WHAT.EDU.VN, we’re here to help! Our platform offers free answers to all your questions. Whether you’re struggling with homework, seeking deeper insights, or simply curious, our community of experts is ready to provide clear, accurate, and helpful responses. Don’t hesitate—visit WHAT.EDU.VN today and get the answers you need!

We understand that finding reliable and quick answers can be challenging. That’s why WHAT.EDU.VN is dedicated to providing a user-friendly platform where you can ask questions and receive timely responses from knowledgeable individuals. Forget about expensive consultations or endless searching; we offer a free service tailored to meet your needs.

Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: WHAT.EDU.VN

Ask your question now and experience the convenience and value of what.edu.vn!