What Is An Exponent? This is a common question, and at WHAT.EDU.VN, we’re here to provide a simple explanation. Exponents, also known as powers, are a shorthand way of showing how many times a number is multiplied by itself. Understanding exponents is essential for various mathematical concepts, from basic arithmetic to advanced algebra. Explore exponential notation, learn about the rules of exponents, and discover how they simplify complex calculations. Need more help? Ask your question for free on WHAT.EDU.VN and get the answers you need.
1. What Are Exponents?
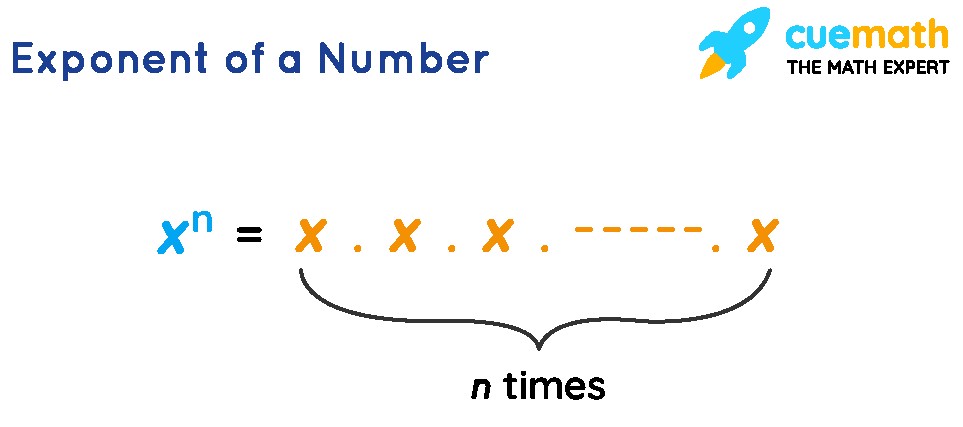
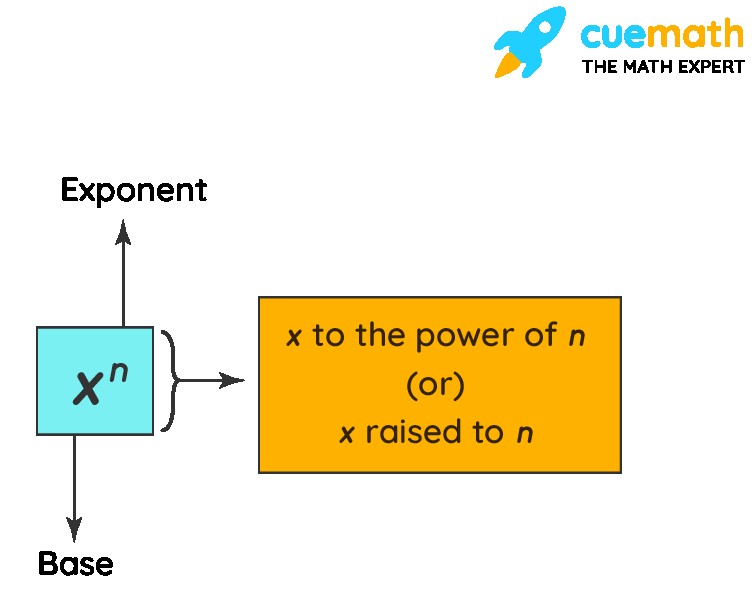
The exponent of a number indicates how many times the base number is multiplied by itself. For example, in the expression 53, the base is 5, and the exponent is 3. This means 5 is multiplied by itself three times: 5 x 5 x 5. The result, 125, is called the power. Understanding exponential notation is crucial in simplifying mathematical expressions and solving equations.
1.1. Delving into the Meaning of Exponents
Exponents provide a concise way to represent repeated multiplication. Instead of writing out a long series of multiplications, you can use exponents to express the same operation more efficiently. The exponential form consists of two parts: the base and the exponent (or power). The base is the number being multiplied, and the exponent indicates how many times the base is multiplied by itself.
For example, consider the expression 2 x 2 x 2 x 2 x 2. This can be written in exponential form as 25, where 2 is the base and 5 is the exponent. This expression is read as “2 to the power of 5” or “2 raised to the 5th power”. The exponent tells us that we are multiplying 2 by itself 5 times.
Key terms in exponential notation include:
- Base: The number being multiplied by itself.
- Exponent (or Power): The number indicating how many times the base is multiplied by itself.
Understanding the meaning of exponents makes it easier to work with large numbers and complex calculations. If you have questions about exponential notation or want to learn more, ask for free on WHAT.EDU.VN and get reliable answers quickly. Our community of experts is ready to help you grasp this fundamental concept.
1.2. Real-World Applications of Exponents
Exponents are more than just a mathematical concept; they have numerous practical applications in various fields. From science and engineering to finance and computer science, exponents help simplify complex calculations and represent large or small quantities efficiently.
One common application is in scientific notation, where exponents are used to express very large or very small numbers. For example, the speed of light is approximately 299,792,458 meters per second. In scientific notation, this is written as 2.99792458 x 108 m/s. The exponent 8 indicates that the decimal point should be moved eight places to the right, making the number easier to work with.
Another example is in compound interest calculations. The formula for compound interest is A = P(1 + r/n)nt, where:
- A is the amount of money accumulated after n years, including interest.
- P is the principal amount (the initial amount of money).
- r is the annual interest rate (as a decimal).
- n is the number of times that interest is compounded per year.
- t is the number of years the money is invested or borrowed for.
The exponent ‘nt’ in this formula shows how the interest is compounded over time, significantly affecting the final amount.
Exponents are also used in computer science to measure storage capacity. For instance, 1 kilobyte (KB) is 210 bytes, 1 megabyte (MB) is 220 bytes, and 1 gigabyte (GB) is 230 bytes.
Understanding these real-world applications highlights the importance of exponents in solving practical problems. If you have specific questions about how exponents are used in your field of interest, ask on WHAT.EDU.VN for free and get detailed explanations from experts.
2. Unveiling the Laws (Properties or Rules) of Exponents
To manipulate and simplify expressions with exponents, it’s essential to understand the fundamental laws or rules of exponents. These rules allow you to combine, divide, and simplify exponential expressions, making complex calculations more manageable. Let’s explore these key properties:
2.1. Core Properties of Exponents
-
Product of Powers Rule: When multiplying two exponential expressions with the same base, you add the exponents. Mathematically, this is expressed as:
am * an = am+n
Example: 23 * 24 = 23+4 = 27 = 128
-
Quotient of Powers Rule: When dividing two exponential expressions with the same base, you subtract the exponents. Mathematically, this is expressed as:
am / an = am-n
Example: 55 / 52 = 55-2 = 53 = 125
-
Power of a Power Rule: When raising an exponential expression to another power, you multiply the exponents. Mathematically, this is expressed as:
(am)n = am*n
Example: (32)3 = 32*3 = 36 = 729
-
Power of a Product Rule: When raising a product to a power, you apply the power to each factor in the product. Mathematically, this is expressed as:
(ab)m = ambm
Example: (2x)3 = 23x3 = 8x3
-
Power of a Quotient Rule: When raising a quotient to a power, you apply the power to both the numerator and the denominator. Mathematically, this is expressed as:
(a/b)m = am / bm
Example: (4/y)2 = 42 / y2 = 16 / y2
-
Zero Exponent Rule: Any non-zero number raised to the power of 0 is equal to 1. Mathematically, this is expressed as:
a0 = 1 (where a ≠ 0)
Example: 70 = 1
-
Negative Exponent Rule: A number raised to a negative exponent is equal to the reciprocal of the number raised to the positive exponent. Mathematically, this is expressed as:
a-m = 1 / am
Example: 4-2 = 1 / 42 = 1 / 16
Understanding and applying these core properties of exponents is essential for simplifying algebraic expressions and solving equations efficiently. If you’re struggling with any of these rules, remember that WHAT.EDU.VN offers a platform where you can ask questions for free and receive detailed explanations from experts. Don’t hesitate to seek help when you need it!
2.2. Utilizing Exponent Rules for Simplification
Mastering the exponent rules is crucial for simplifying complex mathematical expressions. By applying these rules correctly, you can reduce complicated problems to manageable steps. Here are some examples illustrating how to use these rules:
Example 1: Simplifying Expressions with Product and Quotient Rules
Simplify the expression: (x5 y3) / (x2 y)
Solution:
- Apply the product of powers rule to the numerator: x5 * y3 remains as x5y3
- Apply the product of powers rule to the denominator: x2 * y remains as x2y
- Apply the quotient of powers rule to x: x5 / x2 = x5-2 = x3
- Apply the quotient of powers rule to y: y3 / y = y3-1 = y2
- Combine the simplified terms: x3y2
Example 2: Simplifying Expressions with Power of a Power Rule
Simplify the expression: (a2b3)4
Solution:
- Apply the power of a product rule: (a2b3)4 = (a2)4 * (b3)4
- Apply the power of a power rule to a: (a2)4 = a2*4 = a8
- Apply the power of a power rule to b: (b3)4 = b3*4 = b12
- Combine the simplified terms: a8b12
Example 3: Simplifying Expressions with Negative Exponents
Simplify the expression: 3-2 x4 y-1
Solution:
- Apply the negative exponent rule to 3-2: 3-2 = 1 / 32 = 1 / 9
- Apply the negative exponent rule to y-1: y-1 = 1 / y
- Combine the simplified terms: (1 / 9) x4 (1 / y) = x4 / (9y)
Example 4: Simplifying Expressions with Zero Exponents
Simplify the expression: (5a0b2) / (c3)
Solution:
- Apply the zero exponent rule to a0: a0 = 1
- Substitute a0 with 1: (5 1 b2) / (c3)
- Simplify: 5b2 / c3
By practicing these examples and understanding the underlying rules, you can confidently simplify various exponential expressions. If you encounter more complex problems or need further clarification, don’t hesitate to ask your questions for free on WHAT.EDU.VN. Our community is here to support your learning journey.
3. Understanding Negative Exponents
Negative exponents might seem tricky at first, but they are a straightforward way of expressing reciprocals. A negative exponent indicates that you need to take the reciprocal of the base raised to the positive exponent. This concept is essential for simplifying expressions and solving equations involving exponents.
3.1. Converting Negative Exponents to Positive
To convert a negative exponent to a positive exponent, you simply take the reciprocal of the base and change the sign of the exponent. Mathematically, this is represented as:
a-n = 1 / an
Here’s how to apply this rule with examples:
-
Example 1: Convert 2-3 to a positive exponent.
Solution: 2-3 = 1 / 23 = 1 / 8
-
Example 2: Convert x-5 to a positive exponent.
Solution: x-5 = 1 / x5
-
Example 3: Convert (1/3)-2 to a positive exponent.
Solution: (1/3)-2 = (3/1)2 = 32 = 9
-
Example 4: Convert (a/b)-n to a positive exponent.
Solution: (a/b)-n = (b/a)n
These examples demonstrate that a negative exponent signifies taking the reciprocal of the base. This transformation makes it easier to work with exponents and simplify expressions. If you have further questions about negative exponents, remember that WHAT.EDU.VN allows you to ask questions for free and get clear, helpful answers.
3.2. Practical Applications of Negative Exponents
Negative exponents are not just theoretical concepts; they have practical applications in various real-world scenarios. Understanding how to use negative exponents can simplify calculations and provide a more intuitive understanding of certain phenomena.
1. Scientific Notation with Small Numbers
In scientific notation, negative exponents are used to represent very small numbers. For example, the diameter of a human hair is approximately 0.00007 meters. In scientific notation, this is written as 7 x 10-5 meters. The negative exponent -5 indicates that you need to move the decimal point 5 places to the left.
2. Electrical Engineering
In electrical engineering, negative exponents are used to represent small units such as capacitance (measured in farads). For instance, a capacitor might have a capacitance of 1 x 10-6 farads, which is commonly expressed as 1 microfarad (µF).
3. Computer Science
In computer science, negative exponents can be used to represent fractions of a second when dealing with computer processing speeds. For example, a computer might perform an operation in 1 x 10-9 seconds, which is 1 nanosecond.
4. Finance and Interest Rates
Negative exponents can appear in financial calculations, especially when dealing with depreciation or decay rates. For example, if an asset depreciates at a rate of 10% per year, its value after t years can be represented as V = V0(1 – 0.1)t, where V0 is the initial value. If you want to find the value of the asset at a time in the past, you might use a negative value for t.
5. Simplifying Complex Fractions
Negative exponents can also help simplify complex fractions. For example, consider the expression:
(x2y-1) / (x-3y2)
To simplify this, you can rewrite it as:
x2 (1/y) / ((1/x3) y2)
Then, multiply by the reciprocal of the denominator:
x2 (1/y) (x3/y2) = x5 / y3
These examples illustrate how negative exponents are used in real-world contexts to simplify calculations and express quantities in a more manageable form. If you have any questions or need further clarification, remember to ask for free on WHAT.EDU.VN, where experts are ready to assist you.
4. Exploring Exponents with Fractions
Fractional exponents provide a powerful way to express roots and radicals in a concise and manageable format. Understanding how to work with fractional exponents is essential for simplifying algebraic expressions and solving equations involving roots.
4.1. Converting Between Fractional Exponents and Radicals
A fractional exponent can be converted into a radical expression and vice versa. The general rule for this conversion is:
am/n = n√am
Where:
- a is the base
- m is the exponent
- n is the index of the radical
Here are several examples to illustrate the conversion:
-
Example 1: Convert 41/2 to a radical expression.
Solution: 41/2 = √4 = 2. This is the square root of 4.
-
Example 2: Convert 81/3 to a radical expression.
Solution: 81/3 = 3√8 = 2. This is the cube root of 8.
-
Example 3: Convert 272/3 to a radical expression.
Solution: 272/3 = 3√272 = 3√729 = 9. Here, we first square 27 to get 729, then take the cube root.
-
Example 4: Convert 163/4 to a radical expression.
Solution: 163/4 = 4√163 = 4√4096 = 8. Here, we first raise 16 to the power of 3 to get 4096, then take the fourth root.
-
Example 5: Convert √5 to a fractional exponent.
Solution: √5 = 51/2. This is the square root of 5 expressed as a fractional exponent.
-
Example 6: Convert 3√x2 to a fractional exponent.
Solution: 3√x2 = x2/3. This shows how to convert a radical with a variable base to a fractional exponent.
Understanding these conversions allows you to switch between fractional exponents and radicals, choosing the form that is most convenient for the problem you are solving. If you need more examples or have specific questions, ask for free on WHAT.EDU.VN, where experts are ready to provide detailed explanations and assistance.
4.2. Simplifying Expressions with Fractional Exponents
Simplifying expressions with fractional exponents involves applying the rules of exponents and converting between fractional exponents and radicals. This process makes complex calculations easier to manage. Here are some examples illustrating how to simplify such expressions:
Example 1: Simplifying Expressions Using Exponent Rules
Simplify: (x1/2 * x3/4) / x1/4
Solution:
- Apply the product of powers rule: x1/2 * x3/4 = x(1/2 + 3/4) = x5/4
- Apply the quotient of powers rule: x5/4 / x1/4 = x(5/4 – 1/4) = x4/4
- Simplify: x4/4 = x1 = x
Example 2: Converting to Radicals and Simplifying
Simplify: 163/2
Solution:
- Convert to a radical: 163/2 = √163
- Evaluate the square root: √16 = 4
- Raise to the power of 3: 43 = 64
Example 3: Combining Multiple Rules
Simplify: (82/3 * y-1/2)3
Solution:
- Apply the power of a product rule: (82/3 y-1/2)3 = 8(2/3)3 y(-1/2)3 = 82 * y-3/2
- Evaluate 82: 82 = 64
- Apply the negative exponent rule: y-3/2 = 1 / y3/2
- Combine the terms: 64 / y3/2
Example 4: Simplifying Complex Radicals with Fractional Exponents
Simplify: 3√(x6y9)
Solution:
- Convert to fractional exponents: 3√(x6y9) = (x6y9)1/3
- Apply the power of a product rule: (x6y9)1/3 = x6(1/3) y9*(1/3)
- Simplify the exponents: x2y3
By practicing these examples, you’ll become more comfortable simplifying expressions with fractional exponents. If you encounter more challenging problems or need further assistance, remember that WHAT.EDU.VN is here to help. Ask your questions for free and get expert guidance to master this topic.
5. Understanding Decimal Exponents
Decimal exponents may seem complex, but they are simply another way to represent exponents that can be converted into fractional forms. Decimal exponents appear in various mathematical and scientific contexts, making it useful to understand how to work with them.
5.1. Converting Decimal Exponents to Fractions
To work with decimal exponents, the first step is to convert the decimal into a fraction. This makes it easier to apply the rules of exponents and simplify expressions. Here’s how to do it with examples:
-
Example 1: Convert 41.5 to a fractional exponent.
Solution:
- Convert 1.5 to a fraction: 1.5 = 3/2
- Rewrite the expression: 41.5 = 43/2
-
Example 2: Convert 90.5 to a fractional exponent.
Solution:
- Convert 0.5 to a fraction: 0.5 = 1/2
- Rewrite the expression: 90.5 = 91/2
-
Example 3: Convert 80.75 to a fractional exponent.
Solution:
- Convert 0.75 to a fraction: 0.75 = 3/4
- Rewrite the expression: 80.75 = 83/4
-
Example 4: Convert 22.25 to a fractional exponent.
Solution:
- Convert 2.25 to a fraction: 2.25 = 9/4
- Rewrite the expression: 22.25 = 29/4
-
Example 5: Convert 5-0.2 to a fractional exponent.
Solution:
- Convert -0.2 to a fraction: -0.2 = -1/5
- Rewrite the expression: 5-0.2 = 5-1/5
5.2. Solving Expressions with Decimal Exponents
Once you’ve converted the decimal exponent into a fraction, you can simplify the expression using the rules of exponents and radicals. Here are examples illustrating this process:
Example 1: Simplifying 41.5
Solution:
- Convert to fractional exponent: 41.5 = 43/2
- Rewrite as a radical: 43/2 = √43
- Evaluate: √43 = √(444) = √64 = 8
Example 2: Simplifying 90.5
Solution:
- Convert to fractional exponent: 90.5 = 91/2
- Rewrite as a radical: 91/2 = √9
- Evaluate: √9 = 3
Example 3: Simplifying 80.75
Solution:
- Convert to fractional exponent: 80.75 = 83/4
- Rewrite as a radical: 83/4 = 4√83
- Evaluate: 4√83 = 4√512 ≈ 5.657
Example 4: Simplifying 22.25
Solution:
- Convert to fractional exponent: 22.25 = 29/4
- Rewrite as a radical: 29/4 = 4√29
- Evaluate: 4√29 = 4√512 ≈ 4.757
Example 5: Simplifying 5-0.2
Solution:
- Convert to fractional exponent: 5-0.2 = 5-1/5
- Apply the negative exponent rule: 5-1/5 = 1 / 51/5
- Rewrite as a radical: 1 / 51/5 = 1 / 5√5
- Evaluate: 1 / 5√5 ≈ 0.672
By following these steps, you can effectively solve expressions with decimal exponents. If you encounter more complex problems or need further assistance, remember that WHAT.EDU.VN is here to help. Ask your questions for free and get expert guidance to master this topic.
6. The Role of Scientific Notation with Exponents
Scientific notation is a method of expressing very large or very small numbers in a standardized format that makes them easier to handle. Exponents play a critical role in scientific notation, as they represent the power of 10 by which the number is multiplied.
6.1. Writing Numbers in Scientific Notation
Scientific notation expresses a number as a product of two parts: a coefficient (a number between 1 and 10) and a power of 10. The general form is:
a × 10b
Where:
- ‘a’ is the coefficient, and 1 ≤ |a| < 10
- ‘b’ is the exponent, which is an integer
Here’s how to convert numbers into scientific notation:
- Step 1: Place the decimal point after the first non-zero digit.
- Step 2: Count the number of places you moved the decimal point. This number becomes the exponent ‘b’.
- Step 3: If you moved the decimal to the left, the exponent is positive. If you moved it to the right, the exponent is negative.
Examples:
-
Convert 6,500,000 to scientific notation:
Solution:
- Place the decimal after the first non-zero digit: 6.5
- Count the number of places the decimal was moved: 6 places
- Write in scientific notation: 6.5 × 106
-
Convert 0.000042 to scientific notation:
Solution:
- Place the decimal after the first non-zero digit: 4.2
- Count the number of places the decimal was moved: 5 places
- Write in scientific notation: 4.2 × 10-5
-
Convert 1,230 to scientific notation:
Solution:
- Place the decimal after the first non-zero digit: 1.23
- Count the number of places the decimal was moved: 3 places
- Write in scientific notation: 1.23 × 103
-
Convert 0.0000000098 to scientific notation:
Solution:
- Place the decimal after the first non-zero digit: 9.8
- Count the number of places the decimal was moved: 9 places
- Write in scientific notation: 9.8 × 10-9
-
Convert 75,000,000,000 to scientific notation:
Solution:
- Place the decimal after the first non-zero digit: 7.5
- Count the number of places the decimal was moved: 10 places
- Write in scientific notation: 7.5 × 1010
6.2. Performing Calculations with Scientific Notation
Scientific notation simplifies arithmetic operations with very large or very small numbers. Here are the rules for performing multiplication, division, addition, and subtraction:
-
Multiplication:
- Multiply the coefficients.
- Add the exponents.
- (a × 10b) × (c × 10d) = (a × c) × 10(b+d)
-
Division:
- Divide the coefficients.
- Subtract the exponents.
- (a × 10b) / (c × 10d) = (a / c) × 10(b-d)
-
Addition and Subtraction:
- Ensure the numbers have the same exponent.
- Add or subtract the coefficients.
- Keep the same exponent.
- (a × 10b) + (c × 10b) = (a + c) × 10b
- (a × 10b) – (c × 10b) = (a – c) × 10b
Examples:
-
(3 × 105) × (2 × 103)
Solution:
- Multiply the coefficients: 3 × 2 = 6
- Add the exponents: 5 + 3 = 8
- Result: 6 × 108
-
(8 × 107) / (4 × 102)
Solution:
- Divide the coefficients: 8 / 4 = 2
- Subtract the exponents: 7 – 2 = 5
- Result: 2 × 105
-
(5 × 104) + (3 × 104)
Solution:
- Add the coefficients: 5 + 3 = 8
- Keep the same exponent: 104
- Result: 8 × 104
-
(7.2 × 10-3) – (2.1 × 10-3)
Solution:
- Subtract the coefficients: 7.2 – 2.1 = 5.1
- Keep the same exponent: 10-3
- Result: 5.1 × 10-3
-
(4 × 106) + (6 × 105)
Solution:
- Adjust the exponents to be the same: 6 × 105 = 0.6 × 106
- Add the coefficients: 4 + 0.6 = 4.6
- Keep the same exponent: 106
- Result: 4.6 × 106
Using scientific notation and understanding how to perform calculations with it simplifies working with very large and very small numbers. If you encounter more complex problems or need further assistance, remember that WHAT.EDU.VN is here to help. Ask your questions for free and get expert guidance to master this topic.
Navigating exponents doesn’t have to be a solitary journey. At WHAT.EDU.VN, we understand the challenges that come with grasping new concepts. Whether you’re wrestling with the basic principles, exploring the nuances of exponent rules, or seeking practical applications, our platform is designed to offer you the support you need.
Facing tricky exponent problems?
Don’t let complex calculations hold you back. Our community is ready to provide step-by-step solutions and clear explanations, ensuring you not only get the right answer but also understand the underlying principles.
Unsure about a specific rule or concept?
Confusion is a common part of the learning process. WHAT.EDU.VN offers a space to ask any question, no matter how basic or complex. Receive personalized guidance and insights from experienced experts.
Want to see exponents in action?
From scientific notation to real-world applications, we can help you connect the dots and see how exponents are used in various fields.
Ready to take the next step?
Join the WHAT.EDU.VN community today and unlock a world of free, reliable, and expert-driven answers.
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: what.edu.vn
7. FAQs on Exponents
Here are some frequently asked questions about exponents, covering basic definitions, properties, and applications:
| Question | Answer |
|---|---|
| What are exponents in math? | An exponent indicates how many times a number (the base) is multiplied by itself. For example, in 23, 2 is the base, and 3 is the exponent, meaning 2 × 2 × 2 = 8. |
| What are the properties of exponents? | Key properties include the product of powers (am × an = am+n), quotient of powers (am / an = am-n), power of a power ((am)n = amn), and the zero exponent rule (a0 = 1). |
| What are some examples of exponents? | Examples include 32 = 9, 53 = 125, and 24 = 16. These show how the base is multiplied by itself the number of times indicated by the exponent. |
| How do exponents relate to real life? | Exponents are used in scientific notation to represent very large or small numbers, compound interest calculations, computer storage measurements, and more. |
| How do you add exponents? | You can only add exponential expressions if they have the same base and exponent. Otherwise, you cannot directly add exponents; you must simplify each term separately. |
| Why are exponents important? | Exponents provide a concise way to represent repeated multiplication, simplify complex calculations, and express very large or small numbers efficiently. |
| How do you calculate exponents using a calculator? | To calculate exponents, use the “^” or “xy” button on your calculator. Enter the base, press the exponent button, and then enter the exponent. |
| How do you multiply exponents? | When multiplying exponential expressions with the same base, add the exponents: am × an = am+n. For example, 22 × 23 = 25 = 32. |
| What is the use of the properties of exponents? | The properties of exponents simplify complex expressions, making calculations easier and more efficient. They are essential for algebra, calculus, and various scientific and engineering applications. |
| What are the real-life applications of exponents? | Real-life applications include calculating compound interest, measuring the intensity of earthquakes on the Richter scale, determining the growth of populations, and representing data in computer science. |
| How are laws of exponents used in algebra? | Laws of exponents are used to simplify algebraic expressions, solve equations, and work with polynomials. They are fundamental tools in algebraic manipulation and problem-solving. |
| How are negative exponents used in real life? | Negative exponents are used |