Are you curious about What Is An Integer In Math? This comprehensive guide from WHAT.EDU.VN will explore the integer definition, properties, operations, and real-world applications. We aim to provide a clear and concise understanding of integer numbers, ensuring you grasp the fundamentals and even some advanced concepts. Discover integers explained simply, and master integer operations with ease.
1. Understanding Integers: The Basics
1.1. What is an Integer in Math? Defining the Term
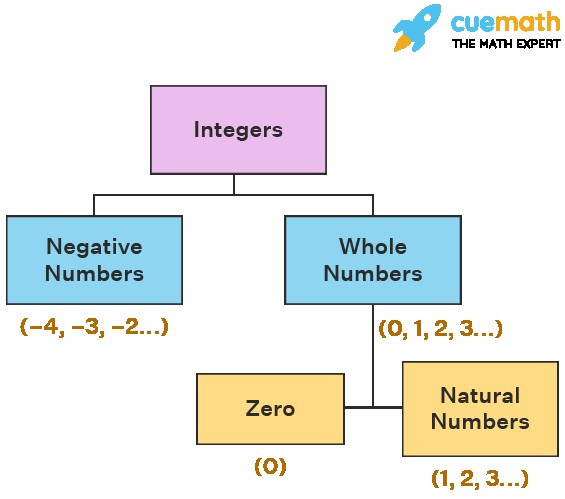
The integer definition is simple: An integer is any whole number (not a fractional number) that can be positive, negative, or zero. Integers don’t include fractions, decimals, or mixed numbers. Think of them as the building blocks of the number system, used for counting, measuring, and representing quantities.
To put it simply, an integer is a number that can be written without a fractional component.
1.2. Positive Integers, Negative Integers, and Zero
Integers are categorized into three distinct groups:
- Positive Integers: These are all whole numbers greater than zero (1, 2, 3, 4, …). They extend infinitely in the positive direction.
- Negative Integers: These are all the opposites of positive integers (-1, -2, -3, -4, …). They extend infinitely in the negative direction.
- Zero (0): Zero is a unique integer that is neither positive nor negative. It sits perfectly in the middle of the number line, separating the positive and negative realms.
1.3 Examples of Integers
Here’s a list of numbers that are integers:
- -100
- -5
- -1
- 0
- 1
- 15
- 200
1.4. Numbers That Are Not Integers
These numbers aren’t integers:
- 1/2 (This is a fraction)
- 0.75 (This is a decimal)
- √2 (This is an irrational number)
- 3.14159 (Pi, another irrational number)
1.3. The Set of Integers: A Formal Representation
In mathematics, the set of all integers is commonly denoted by the symbol “Z” (from the German word “Zahlen,” meaning “numbers”). This set includes all positive and negative whole numbers, as well as zero:
Z = {…, -3, -2, -1, 0, 1, 2, 3, …}
This set extends infinitely in both the positive and negative directions, encompassing all possible integer values.
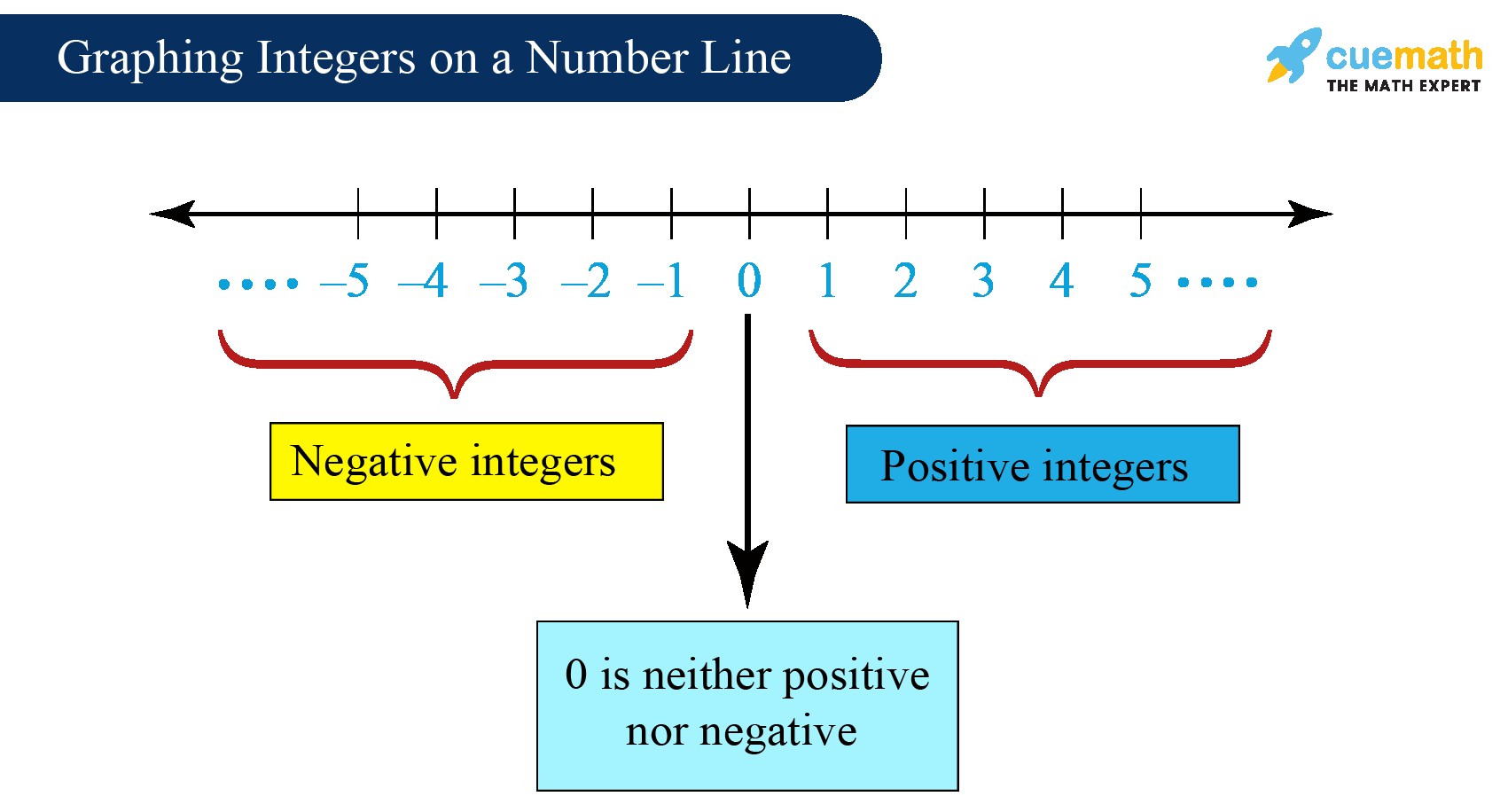
2. Visualizing Integers: The Number Line
2.1. Representing Integers on a Number Line
The number line is a powerful visual tool for understanding and comparing integers. It’s a straight line where numbers are placed at equal intervals. Zero sits at the center, with positive integers extending to the right and negative integers extending to the left.
2.2. Key Principles for Number Line Representation
When placing integers on a number line, remember these core principles:
- Magnitude: The farther a number is from zero, the greater its absolute value (magnitude).
- Direction: Numbers to the right of zero are positive, while numbers to the left are negative.
- Order: Numbers increase in value as you move from left to right on the number line.
2.3. How to Graph Integers on a Number Line
To graph an integer on a number line, simply locate its position based on its value and place a dot or mark at that point.
- Example: To graph the integer -3, find the point three units to the left of zero and mark it.
2.4. Using the Number Line for Comparison
The number line is incredibly useful for comparing integers. Remember:
- Any number to the right of another number is greater.
- Any number to the left of another number is smaller.
For example, -1 is greater than -5 because -1 lies to the right of -5 on the number line.
3. Performing Operations with Integers
Integers can be used in all basic arithmetic operations: addition, subtraction, multiplication, and division. However, there are certain rules to follow when dealing with negative numbers.
3.1. Addition of Integers: Combining Values
Adding integers involves combining their values to find the total sum.
3.1.1. Rules for Integer Addition
- Same Signs: If both integers have the same sign (both positive or both negative), add their absolute values and keep the same sign.
- Example: 3 + 5 = 8 (both positive, result is positive)
- Example: -2 + (-4) = -6 (both negative, result is negative)
- Different Signs: If the integers have different signs (one positive and one negative), subtract the smaller absolute value from the larger absolute value. The result takes the sign of the integer with the larger absolute value.
- Example: -7 + 3 = -4 (7 is larger, and it’s negative)
- Example: 6 + (-2) = 4 (6 is larger, and it’s positive)
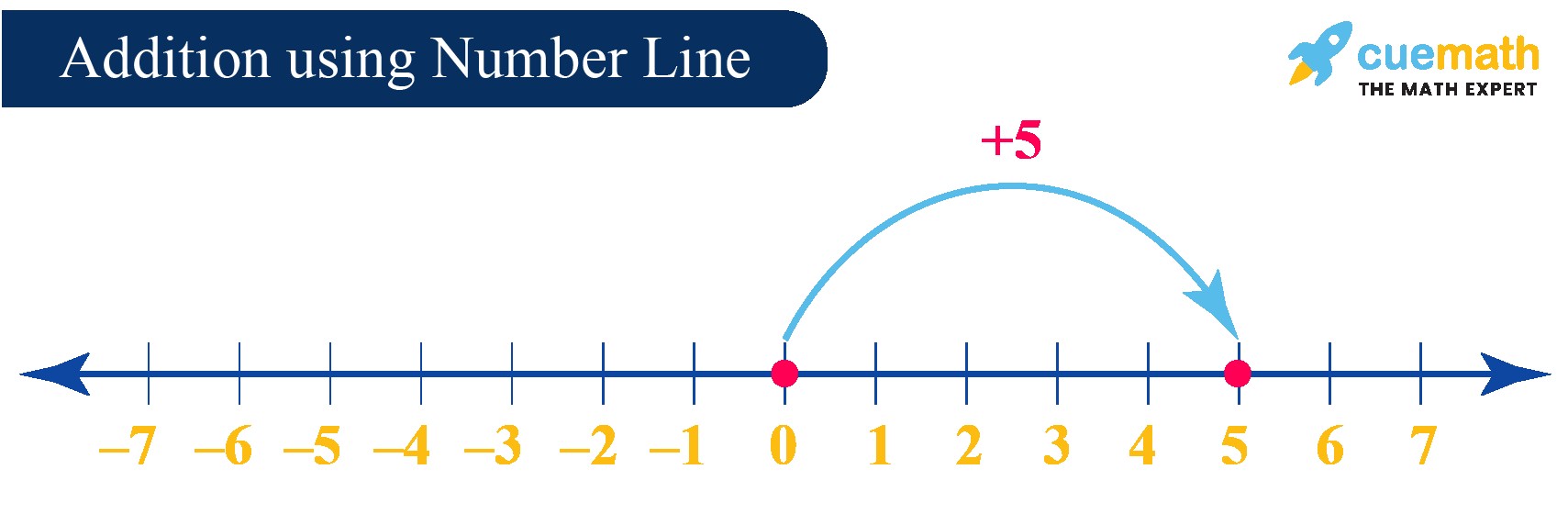
3.1.2. Addition on the Number Line
You can also visualize addition on the number line:
- Start at the first integer.
- If you’re adding a positive integer, move to the right.
- If you’re adding a negative integer, move to the left.
- The final position is the sum.
3.2. Subtraction of Integers: Finding the Difference
Subtracting integers involves finding the difference between their values.
3.2.1. The “Add the Opposite” Rule
The key to subtracting integers is to convert the subtraction problem into an addition problem by “adding the opposite.”
- Example: 5 – 3 becomes 5 + (-3)
- Example: -2 – (-4) becomes -2 + 4
3.2.2. Applying Addition Rules
Once you’ve converted the subtraction to addition, simply follow the addition rules outlined above.
3.3. Multiplication of Integers: Repeated Addition
Multiplying integers is essentially repeated addition.
3.3.1. Multiplication Sign Rules
The most important thing to remember with multiplication is the sign rules:
- Positive × Positive = Positive
- Negative × Negative = Positive
- Positive × Negative = Negative
- Negative × Positive = Negative
Here is a table summarizing these rules:
| Factor 1 | Factor 2 | Product | Example |
|---|---|---|---|
| Positive | Positive | Positive | 2 × 3 = 6 |
| Positive | Negative | Negative | 2 × (-3) = -6 |
| Negative | Positive | Negative | (-2) × 3 = -6 |
| Negative | Negative | Positive | (-2) × (-3) = 6 |
3.3.2. Applying the Rules
To multiply integers:
-
Multiply their absolute values.
-
Apply the appropriate sign rule.
- Example: -4 × 2 = -8 (Negative × Positive = Negative)
- Example: -3 × -5 = 15 (Negative × Negative = Positive)
3.4. Division of Integers: Equal Grouping
Dividing integers involves splitting one integer into equal groups determined by another integer.
3.4.1. Division Sign Rules
The sign rules for division are the same as for multiplication:
- Positive ÷ Positive = Positive
- Negative ÷ Negative = Positive
- Positive ÷ Negative = Negative
- Negative ÷ Positive = Negative
Here is a table summarizing these rules:
| Dividend | Divisor | Quotient | Example |
|---|---|---|---|
| Positive | Positive | Positive | 12 ÷ 3 = 4 |
| Positive | Negative | Negative | 12 ÷ (-3) = -4 |
| Negative | Positive | Negative | (-12) ÷ 3 = -4 |
| Negative | Negative | Positive | (-12) ÷ (-3) = 4 |
3.4.2. Applying the Rules
To divide integers:
-
Divide their absolute values.
-
Apply the appropriate sign rule.
- Example: 10 ÷ -2 = -5 (Positive ÷ Negative = Negative)
- Example: -15 ÷ -3 = 5 (Negative ÷ Negative = Positive)
4. Exploring Properties of Integers
Integers possess several fundamental properties that govern how they behave under mathematical operations. These properties are crucial for understanding and manipulating integers effectively.
4.1. Closure Property
The closure property states that when you perform a specific operation on any two integers, the result will also be an integer.
- Addition: If a and b are integers, then a + b is also an integer.
- Subtraction: If a and b are integers, then a – b is also an integer.
- Multiplication: If a and b are integers, then a × b is also an integer.
Note: The integers are NOT closed under division, because dividing two integers doesn’t always result in another integer (e.g., 1 ÷ 2 = 0.5, and 0.5 is not an integer).
4.2. Associative Property
The associative property states that when adding or multiplying three or more integers, the grouping of the integers does not affect the result.
- Addition: a + (b + c) = (a + b) + c
- Multiplication: a × (b × c) = (a × b) × c
4.3. Commutative Property
The commutative property states that when adding or multiplying two integers, the order of the integers does not affect the result.
- Addition: a + b = b + a
- Multiplication: a × b = b × a
4.4. Distributive Property
The distributive property combines multiplication and addition. It states that multiplying an integer by the sum of two other integers is the same as multiplying the integer by each of the other integers individually and then adding the products.
- a × (b + c) = (a × b) + (a × c)
4.5. Identity Property
The identity property defines special numbers that, when used in an operation, leave the original number unchanged.
- Additive Identity: Zero (0) is the additive identity because adding zero to any integer does not change the integer’s value (a + 0 = a).
- Multiplicative Identity: One (1) is the multiplicative identity because multiplying any integer by one does not change the integer’s value (a × 1 = a).
4.6. Inverse Property
The inverse property defines numbers that, when combined with another number using a specific operation, result in the identity element.
- Additive Inverse: For any integer a, its additive inverse is -a because a + (-a) = 0.
- Multiplicative Inverse: For any non-zero integer a, its multiplicative inverse is 1/a because a × (1/a) = 1.
5. Integers in the Real World
Integers aren’t just abstract mathematical concepts; they’re used extensively in everyday life.
5.1. Temperature Measurement
Temperature is often measured in degrees Celsius or Fahrenheit, which can be positive, negative, or zero. Negative temperatures are represented using negative integers. For instance, -5°C indicates a temperature 5 degrees below zero Celsius.
5.2. Financial Transactions
Integers are fundamental to financial accounting. Bank accounts use positive integers to represent deposits (credits) and negative integers to represent withdrawals (debits). An account balance can be a positive or negative integer, indicating whether you have money or owe money.
5.3. Altitude and Depth
Altitude (height above sea level) is typically represented using positive integers, while depth (distance below sea level) is represented using negative integers. For example, a mountain peak might have an altitude of 3,000 meters (3,000), while a submarine might be at a depth of -200 meters (-200).
5.4. Sports and Games
Integers are used in many sports and games to track scores, points, and rankings. For example, in golf, scores relative to par (the expected number of strokes for a hole or round) are often expressed as positive or negative integers. A score of -2 indicates two strokes under par, while a score of +3 indicates three strokes over par.
5.5. Time Zones
Time zones around the world are often expressed as offsets from Coordinated Universal Time (UTC). These offsets are represented using integers. For instance, Eastern Standard Time (EST) is UTC-5, meaning it is 5 hours behind UTC.
6. Commonly Asked Questions About Integers
6.1. What is an Integer in Math?
An integer is a whole number (not a fraction) that can be positive, negative, or zero. Integers do not include decimals or fractions. Examples: -3, -2, -1, 0, 1, 2, 3
6.2. Are All Whole Numbers Integers?
Yes, all whole numbers are integers. Whole numbers are non-negative integers (0, 1, 2, 3, …).
6.3. Are All Natural Numbers Integers?
Yes, all natural numbers are integers. Natural numbers are positive integers (1, 2, 3, …).
6.4. Is Zero an Integer?
Yes, zero is an integer. It is neither positive nor negative.
6.5. Is a Fraction an Integer?
No, a fraction is not an integer. Fractions represent parts of a whole, while integers are whole numbers.
6.6. Is a Decimal an Integer?
No, a decimal is not an integer (unless it terminates and has no fractional part). Decimals represent numbers that are not whole.
6.7. What is a Negative Integer?
A negative integer is an integer that is less than zero. Examples: -1, -2, -3, -4, …
6.8. What is a Positive Integer?
A positive integer is an integer that is greater than zero. Examples: 1, 2, 3, 4, …
6.9. How Do You Add Integers with Different Signs?
To add integers with different signs, subtract the smaller absolute value from the larger absolute value. The result takes the sign of the integer with the larger absolute value.
- Example: -7 + 3 = -4 (7 is larger, and it’s negative)
6.10. How Do You Multiply Integers with Different Signs?
When multiplying integers with different signs, the result is always negative.
- Example: -4 × 2 = -8
6.11. What are Consecutive Integers?
Consecutive integers are integers that follow each other in order, each differing from the previous number by 1. Examples: 5, 6, 7, and 8.
6.12. Why is it Important to Understand Integers?
Understanding integers is essential for building a strong foundation in mathematics. Integers are used in various mathematical concepts, including algebra, geometry, and calculus. Furthermore, integers are widely used in real-world applications, such as finance, science, and technology.
7. Practice Problems
Test your knowledge with these practice problems:
- Add: -8 + 5
- Subtract: 3 – (-2)
- Multiply: -6 × -4
- Divide: 20 ÷ -5
- Simplify: 2 × (3 + -5)
8. Master Integers with WHAT.EDU.VN
Understanding what is an integer in math is fundamental to mathematical proficiency. This guide has covered the basics, operations, properties, and applications of integers. If you’re still struggling or have more questions, don’t hesitate to reach out to WHAT.EDU.VN for personalized assistance.
We understand that finding answers to your questions can be challenging. You might not know who to ask or where to look for reliable information. The good news is WHAT.EDU.VN is here to help.
Do you have questions about math, science, history, or any other subject? Don’t let your curiosity go unanswered. At WHAT.EDU.VN, we provide a platform where you can ask any question and receive prompt, accurate, and easy-to-understand answers. Our community of experts and knowledgeable users are eager to assist you.
Why Choose WHAT.EDU.VN?
- Free Access: Our question-and-answer platform is completely free to use.
- Fast Responses: Get answers to your questions quickly.
- Expert Assistance: Connect with experts in various fields.
- Easy to Use: Our platform is designed to be user-friendly and intuitive.
Ready to get started? Visit WHAT.EDU.VN today and ask your question! We’re here to help you learn and grow.
Contact us:
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: what.edu.vn
Don’t wait any longer. Your answers are just a click away! Ask your question now and let us help you unlock the world of knowledge.