What is an integer? In mathematics, integers are fundamental building blocks. This comprehensive guide, brought to you by WHAT.EDU.VN, will explore integer definition, integer examples, and integer applications, making the world of numbers accessible to everyone. Discover integer properties and integer operations explained simply.
1. Understanding What Is an Integer: The Basics
The term “integer” originates from the Latin word “integer,” meaning whole or intact. So, what is an integer? An integer is any number that’s not a fraction or a decimal. They can be positive, negative, or zero. Integers form the foundation for various mathematical operations and concepts.
Integers are members of the set of whole numbers, consisting of:
- Positive numbers: 1, 2, 3, 4, 5, and so on.
- Negative numbers: -1, -2, -3, -4, -5, and so on.
- Zero: 0, which is neither positive nor negative.
Integers are symbolized by “Z“.
Z= {……-8,-7,-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8,……}
Integers are essential for counting, measuring, and performing arithmetic operations. Understanding integers provides a solid base for further mathematical exploration.
2. Diving Deeper: Types of Integers
Integers come in three distinct flavors: positive integers, negative integers, and zero. Each plays a crucial role in the number system.
2.1. Positive Integers
These are the natural numbers or counting numbers you first learn. Positive integers are greater than zero and extend infinitely.
Z+ → 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30,…
They represent quantities you can count, like apples, books, or friends.
2.2. Negative Integers
Negative integers are less than zero. They are the additive inverses of positive integers.
Z– → -1, -2, -3, -4, -5, -6, -7, -8, -9, -10, -11, -12, -13, -14, -15, -16, -17, -18, -19, -20, -21, -22, -23, -24, -25, -26, -27, -28, -29, -30,…
Think of them as debts, temperatures below zero, or positions below sea level.
2.3. Zero
Zero is a unique integer. It is neither positive nor negative. Zero represents the absence of quantity or a neutral point on the number line.
Zero’s properties make it essential in arithmetic and algebra.
3. Visualizing Integers: The Number Line
A number line is a visual representation of integers, making it easier to understand their order and relationships.
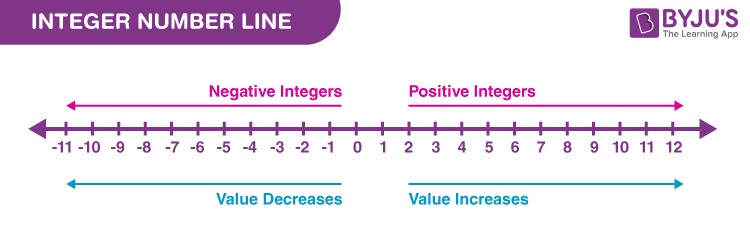Integers on number line
- Zero sits in the middle.
- Positive integers extend to the right, increasing in value.
- Negative integers extend to the left, decreasing in value.
The number line helps visualize integer operations like addition and subtraction. Moving right on the line represents addition, while moving left represents subtraction.
4. Mastering Operations: Arithmetic with Integers
Integers can be added, subtracted, multiplied, and divided. Understanding the rules for these operations is essential.
4.1. Adding Integers
-
Adding integers with the same sign: Add their absolute values and keep the same sign.
- Example: (+3) + (+5) = +8
- Example: (-2) + (-4) = -6
-
Adding integers with different signs: Subtract the smaller absolute value from the larger absolute value. Use the sign of the integer with the larger absolute value.
- Example: (-7) + (+3) = -4 (Since 7 > 3, and 7 is negative)
- Example: (+9) + (-2) = +7 (Since 9 > 2, and 9 is positive)
4.2. Subtracting Integers
To subtract integers, change the sign of the integer being subtracted and then add.
- Example: (+5) – (+2) = (+5) + (-2) = +3
- Example: (-3) – (+1) = (-3) + (-1) = -4
- Example: (+4) – (-2) = (+4) + (+2) = +6
- Example: (-6) – (-5) = (-6) + (+5) = -1
4.3. Multiplying Integers
-
Multiplying integers with the same sign: The result is always positive.
- Example: (+4) x (+3) = +12
- Example: (-2) x (-5) = +10
-
Multiplying integers with different signs: The result is always negative.
- Example: (+6) x (-1) = -6
- Example: (-3) x (+7) = -21
Here’s a table summarizing multiplication rules:
| Multiplication of Signs | Resulting Sign | Examples |
|---|---|---|
| + × + | + | 3 × 4 = 12 |
| + × – | – | 3 × -4 = -12 |
| – × + | – | -3 × 4 = -12 |
| – × – | + | -3 × -4 = 12 |
4.4. Dividing Integers
The rules for dividing integers are similar to multiplication.
-
Dividing integers with the same sign: The result is positive.
- Example: (+10) ÷ (+2) = +5
- Example: (-8) ÷ (-4) = +2
-
Dividing integers with different signs: The result is negative.
- Example: (+12) ÷ (-3) = -4
- Example: (-15) ÷ (+5) = -3
Here’s a table summarizing division rules:
| Division of Signs | Resulting sign | Examples |
|---|---|---|
| + ÷ + | + | 15 ÷ 3 = 5 |
| + ÷ – | – | 15 ÷ -3 = -5 |
| – ÷ + | – | -15 ÷ 3 = -5 |
| – ÷ – | + | -15 ÷ -3 = 5 |
5. Exploring Properties: The Laws of Integers
Integers follow specific properties that govern how they behave under arithmetic operations.
5.1. Closure Property
When two integers are added or multiplied, the result is always another integer.
-
a + b = integer
-
a x b = integer
-
Example: 4 + 7 = 11 (an integer)
-
Example: 3 x 5 = 15 (an integer)
5.2. Commutative Property
The order in which integers are added or multiplied does not affect the result.
-
a + b = b + a
-
a x b = b x a
-
Example: 2 + 6 = 6 + 2 = 8
-
Example: 4 x 9 = 9 x 4 = 36
This property does not apply to subtraction or division.
5.3. Associative Property
When adding or multiplying three or more integers, the grouping does not affect the result.
-
a + (b + c) = (a + b) + c
-
a x (b x c) = (a x b) x c
-
Example: 1 + (2 + 3) = (1 + 2) + 3 = 6
-
Example: 2 x (3 x 4) = (2 x 3) x 4 = 24
Again, this property does not apply to subtraction or division.
5.4. Distributive Property
Multiplication distributes over addition.
a x (b + c) = (a x b) + (a x c)
Example: 2 x (3 + 4) = (2 x 3) + (2 x 4) = 14
5.5. Additive Inverse Property
Every integer has an additive inverse, which, when added to the original integer, results in zero.
a + (-a) = 0
- Example: 5 + (-5) = 0. So, -5 is the additive inverse of 5.
5.6. Multiplicative Inverse Property
Every integer has a multiplicative inverse, which, when multiplied to the original integer, results in one.
a x (1/a) = 1
- Example: 5 x (1/5) = 1. So, 1/5 is the multiplicative inverse of 5.
5.7. Identity Property
-
Additive Identity: Adding zero to any integer does not change the integer’s value.
- a + 0 = a
- Example: 7 + 0 = 7
-
Multiplicative Identity: Multiplying any integer by one does not change the integer’s value.
- a x 1 = a
- Example: 4 x 1 = 4
6. Real-World Relevance: Applications of Integers
Integers are not abstract concepts. They appear everywhere in daily life.
- Temperature: Temperatures above zero are positive integers, while temperatures below zero are negative integers.
- Finance: Credits are positive integers, while debits are negative integers.
- Altitude: Heights above sea level are positive integers, while depths below sea level are negative integers.
- Sports: Scores in many games use integers to represent points for and against a team.
- Construction: Integers are used to measure dimensions, depths, and heights.
- Computer Science: Representing data, counting, and performing calculations in software development and algorithms
Integers are essential for describing and quantifying the world around us.
7. Examples of Integers
Let’s work through a few examples to solidify your understanding.
Example 1:
Plot the following integers on the number line:
-121, -97, -82, -67, -43, -10, 0, 10, 36, 55, 64, 77, 110, 126, 147.
Solution:
In the above number line, each number has been plotted with a red dot.
Example 2:
Solve the following:
- 5 + 3 = ?
- 5 + (-3) = ?
- (-5) + (-3) = ?
- (-5) x (-3) = ?
Solution:
- 5 + 3 = 8
- 5 + (-3) = 5 – 3 = 2
- (-5) + (-3) = -5 – 3 = -8
- (-5) x (-3) = 15
Example 3:
Solve the following product of integers:
- (+5) × (+10)
- (12) × (5)
- (- 5) × (7)
- 5 × (-4)
Solution:
- (+5) × (+10) = +50
- (12) × (5) = 60
- (- 5) × (7) = -35
- 5 × (-4) = -20
Example 4:
Solve the following division of integers:
- (-9) ÷ (-3)
- (-18) ÷ (3)
- (4000) ÷ (- 100)
Solution:
- (-9) ÷ (-3) = 3
- (-18) ÷ (3) = -6
- (4000) ÷ (- 100) = -40
8. Test Your Knowledge: Practice Questions
Test your understanding of integers with these practice questions.
- The sum of two negative integers is always a negative integer. True or false?
- What is the additive inverse of -15?
- Calculate: (-8) x (+4) ÷ (-2)
- Plot the integers from -5 to +5 on the number line.
- What is the sum of the first five negative integers?
- What is the product of the first three positive odd integers?
- If a = -3, b = 5 and c = -2, evaluate a x (b + c).
- Is the division of two integers always an integer? Give an example to support your answer.
- Explain the difference between the commutative property and the associative property with respect to integers.
- Give three real-world examples where negative integers are used.
9. Frequently Asked Questions (FAQs) About Integers
Let’s address some common questions about integers.
9.1. What are integers?
Integers are whole numbers (not fractions) that can be positive, negative, or zero. They are the foundation of many mathematical concepts.
9.2. What is an integer formula?
An integer does not have a formula. Instead, it is a set of positive and negative numbers along with zero.
9.3. What are some examples of integers?
Examples of integers include: -10, -5, 0, 3, 7, 100, and -1000. Numbers like 2.5, 1/2, or π are not integers.
9.4. Can integers be negative?
Yes, integers can be negative. Negative integers are any whole number less than zero.
9.5. What are the types of integers?
There are three types of integers: positive integers, negative integers, and zero.
10. Beyond the Basics: Advanced Integer Concepts
Once you’ve mastered the basics, you can explore more advanced concepts involving integers.
- Number Theory: Integers are fundamental to number theory, which deals with the properties and relationships of numbers.
- Modular Arithmetic: This involves integers and remainders after division, used in cryptography and computer science.
- Algebraic Equations: Integers are used to solve equations and inequalities.
- Coordinate Geometry: Integers are used as coordinates to plot points on a graph.
11. The Power of Asking: Get Your Questions Answered on WHAT.EDU.VN
Still have questions about what is an integer, integer operations, or anything else? Don’t hesitate to ask! WHAT.EDU.VN is here to help. We understand the challenges students, professionals, and curious minds face when seeking quick, reliable answers.
Are you struggling to grasp a concept? Do you have a burning question that needs an expert answer? Our platform offers:
- Free Questioning: Ask any question, no matter how simple or complex, and receive answers from knowledgeable individuals.
- Fast Responses: Get the answers you need quickly, so you can keep learning and moving forward.
- Expert Insights: Connect with experts in various fields who can provide clear, accurate explanations.
- Community Support: Engage with a community of learners and knowledge-seekers.
12. Ready to Ask? Join WHAT.EDU.VN Today!
Don’t let your questions go unanswered. Join WHAT.EDU.VN and experience the ease and convenience of getting free, expert advice at your fingertips.
We’re here to help bridge the gap between curiosity and understanding. Whether you’re a student tackling tough homework, a professional seeking clarity on a work-related issue, or simply a curious individual eager to learn, WHAT.EDU.VN is your go-to resource.
Visit us today and discover the power of asking!
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: WHAT.EDU.VN
Don’t stay puzzled – ask away! Let what.edu.vn be your partner in learning and discovery.
