What Is An Obtuse Angle? WHAT.EDU.VN explains obtuse angles simply, helping you grasp this geometry concept easily. Find fast, free answers to all your questions, and discover how obtuse angles function within shapes, offering a clear understanding of mathematical principles and practical applications. Delve into obtuse angles, supplementary angles, and geometrical shapes!
1. Understanding What Is An Obtuse Angle
In geometry, an obtuse angle is defined as an angle that measures greater than 90° but less than 180°. It’s larger than a right angle but smaller than a straight angle. Think of it as an angle that’s “wider” than a corner but not quite a flat line. Obtuse angles are fundamental in geometry and trigonometry, influencing the properties of various shapes and structures.
2. Key Characteristics of Obtuse Angles
To fully understand what constitutes an obtuse angle, let’s explore its defining characteristics.
2.1. Angle Measurement
The primary characteristic is its measurement. An obtuse angle’s measure falls strictly between 90° and 180°. Any angle that measures exactly 90° is a right angle, and any angle exactly 180° is a straight angle.
2.2. Visual Appearance
Visually, an obtuse angle appears “open” wider than a right angle. Imagine a door opened more than halfway from being closed but not fully extended to form a straight line; that’s akin to the visual representation of an obtuse angle.
2.3. Context within Shapes
Obtuse angles often play significant roles within polygons, particularly triangles and quadrilaterals, influencing their overall shape and properties.
3. Obtuse Angles in Triangles
Triangles are classified based on their angles, and the presence of an obtuse angle leads to a specific type of triangle.
3.1. Obtuse Triangles Defined
An obtuse triangle is a triangle in which one of the angles is an obtuse angle. The other two angles must be acute angles (less than 90°) because the sum of angles in a triangle is always 180°.
3.2. Properties of Obtuse Triangles
- One Obtuse Angle: By definition, an obtuse triangle has one angle greater than 90°.
- Two Acute Angles: The remaining two angles are acute, ensuring the total sum is 180°.
- Longest Side: The side opposite the obtuse angle is the longest side of the triangle.
- Height Location: The altitude (height) from one of the acute angles may fall outside the triangle.
3.3. Types of Obtuse Triangles
Obtuse triangles can be further classified by their sides:
- Obtuse Isosceles Triangle: This triangle has one obtuse angle and two equal sides (and therefore two equal angles, which must be acute).
- Obtuse Scalene Triangle: This triangle has one obtuse angle and all three sides of different lengths.
4. Obtuse Angles in Quadrilaterals
Quadrilaterals, or four-sided polygons, can also feature obtuse angles. Here, we’ll look at how obtuse angles appear in specific types of quadrilaterals.
4.1. Rhombuses
A rhombus is a quadrilateral with all four sides equal in length. The opposite angles are equal, and in a non-square rhombus, two angles are acute, and two are obtuse.
4.2. Parallelograms
A parallelogram has opposite sides that are parallel and equal in length. Like a rhombus, a non-rectangular parallelogram has two acute and two obtuse angles, which are opposite each other.
4.3. Kites
A kite is a quadrilateral with two pairs of adjacent sides that are equal in length. Depending on the specific kite, it may have one or two obtuse angles.
4.4. Trapezoids
A trapezoid (or trapezium) has at least one pair of parallel sides. It can have one or two obtuse angles, depending on its specific configuration.
5. Real-World Examples of Obtuse Angles
Obtuse angles aren’t confined to textbooks; they’re all around us. Recognizing them in everyday objects can solidify your understanding.
5.1. Furniture Design
The recline in a comfortable chair can form an obtuse angle. Similarly, some lamp stands and shelving units may incorporate obtuse angles for aesthetic or functional purposes.
5.2. Architecture
Roof angles often exceed 90 degrees, particularly in designs aimed at maximizing interior space or creating a specific aesthetic. These angles are technically obtuse.
5.3. Sports Equipment
The angle of a baseball bat at the point of contact with the ball can be obtuse, influencing the trajectory and power of the hit. Similarly, the angle of a hockey stick or golf club during a swing can also create obtuse angles.
5.4. Nature
Branches extending from a tree trunk can sometimes form obtuse angles. Additionally, certain rock formations and geological features may naturally display obtuse angles.
6. Measuring Obtuse Angles
Accurately measuring angles is crucial in geometry and practical applications. A protractor is the standard tool for this purpose.
6.1. Using a Protractor
- Placement: Align the base of the protractor along one side of the angle, with the center of the protractor at the angle’s vertex.
- Reading: Find where the other side of the angle intersects the protractor’s scale. Read the degree measurement, ensuring you choose the appropriate scale (inner or outer) based on whether the angle opens from 0 degrees.
- Verification: Ensure the reading is between 90° and 180° for an obtuse angle.
6.2. Digital Tools
Digital protractors or angle measurement apps on smartphones can also measure angles accurately. These tools often use the device’s camera and sensors to calculate the angle.
7. Calculating Unknown Angles
Understanding the relationships between angles allows you to calculate unknown angles, particularly in triangles and quadrilaterals.
7.1. Triangles
Since the sum of angles in a triangle is 180°, if you know two angles, you can find the third by subtracting the sum of the known angles from 180°.
7.2. Quadrilaterals
The sum of angles in a quadrilateral is 360°. If you know three angles, subtract their sum from 360° to find the fourth angle.
7.3. Supplementary Angles
Supplementary angles add up to 180°. If an obtuse angle forms a straight line with another angle, you can find the measure of the other angle by subtracting the obtuse angle from 180°.
8. Obtuse Angles in Trigonometry
Trigonometry extends the study of angles and their relationships to the sides of triangles.
8.1. Trigonometric Functions
When dealing with obtuse angles in trigonometry, trigonometric functions like sine, cosine, and tangent behave differently compared to acute angles. For instance, the cosine of an obtuse angle is negative.
8.2. Unit Circle
The unit circle is a valuable tool for understanding trigonometric functions for angles greater than 90°. It helps visualize the signs and values of trigonometric functions in different quadrants.
8.3. Applications
Obtuse angles are crucial in various applications of trigonometry, such as navigation, physics (projectile motion), and engineering (structural analysis).
9. Common Mistakes to Avoid
When working with obtuse angles, several common mistakes can occur.
9.1. Confusing with Acute Angles
Always verify that the angle measures more than 90° to avoid confusing obtuse angles with acute angles (less than 90°).
9.2. Incorrect Protractor Usage
Ensure the protractor is correctly aligned with the vertex and base of the angle to obtain accurate measurements.
9.3. Miscalculating Angles in Shapes
Double-check your calculations when finding unknown angles in triangles or quadrilaterals to avoid errors.
9.4. Ignoring Trigonometric Signs
Remember that trigonometric functions of obtuse angles may have different signs than those of acute angles.
10. Advanced Concepts Involving Obtuse Angles
For those looking to delve deeper, here are some advanced concepts.
10.1. Law of Cosines
The law of cosines is used to find the sides or angles of a triangle when you know either three sides or two sides and an included angle. It is especially useful in obtuse triangles.
10.2. Vector Analysis
In physics and engineering, obtuse angles are important in vector analysis when resolving forces or velocities into components.
10.3. Spherical Geometry
Obtuse angles also appear in spherical geometry, where the geometry is studied on the surface of a sphere, and the angles can be quite different from planar geometry.
11. Practical Exercises to Reinforce Learning
To solidify your understanding of obtuse angles, try these exercises.
11.1. Angle Identification
Identify which of the following angles are obtuse: 85°, 95°, 120°, 180°, 60°, 150°.
11.2. Triangle Classification
Classify the following triangles based on their angles:
- Triangle with angles 30°, 60°, 90°
- Triangle with angles 45°, 45°, 90°
- Triangle with angles 30°, 30°, 120°
11.3. Angle Calculation
In a triangle, if two angles are 25° and 35°, what is the measure of the third angle? Is it obtuse?
11.4. Real-World Recognition
Find and photograph five examples of obtuse angles in everyday objects around you.
12. FAQ: Obtuse Angles
Q1: Can a triangle have more than one obtuse angle?
No, a triangle can have only one obtuse angle. If it had two, the sum of the angles would exceed 180°, violating the basic property of triangles.
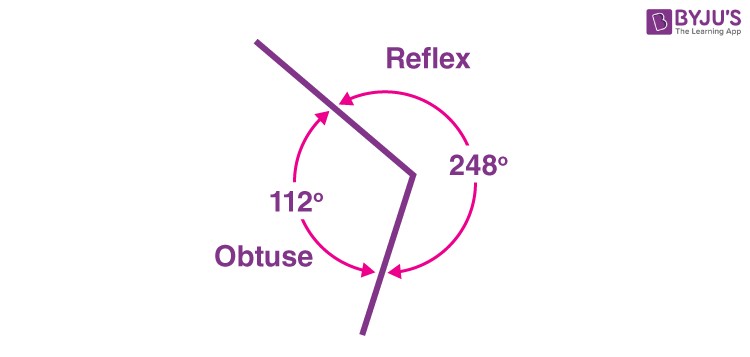
Q2: What is the difference between an obtuse angle and a reflex angle?
An obtuse angle measures between 90° and 180°, while a reflex angle measures between 180° and 360°.
Q3: Are all angles in a parallelogram obtuse?
No, a parallelogram has two acute angles and two obtuse angles, which are opposite each other.
Q4: How can you find an obtuse angle using trigonometric functions?
You can use inverse trigonometric functions. For example, if you know the cosine of an angle is negative, you can use the inverse cosine function to find the obtuse angle.
Q5: What tools can be used to measure obtuse angles accurately?
A protractor is the most common tool, but digital protractors and angle measurement apps are also available for precise measurements.
13. Obtuse Angles in Construction and Engineering
Obtuse angles play a vital role in construction and engineering projects, where structural stability and design aesthetics are critical.
13.1. Roof Design
In roof construction, obtuse angles can be used to create visually appealing and structurally sound designs. The angle of the roof affects its ability to withstand weather conditions such as snow and rain. Architects and engineers carefully calculate these angles to ensure the roof’s longevity and effectiveness.
13.2. Bridge Construction
Bridges often incorporate obtuse angles in their support structures to distribute weight and maintain stability. The angles at which beams and supports are connected are crucial for the bridge’s overall integrity. Engineers use precise measurements and calculations to ensure these angles meet safety standards.
13.3. Furniture Design
Furniture designers use obtuse angles to create comfortable and ergonomic pieces. The angle of a chair’s backrest or the slope of a desk can significantly impact comfort and usability. By understanding and applying the principles of obtuse angles, designers can create furniture that is both functional and aesthetically pleasing.
14. The Significance of Obtuse Angles in Art and Design
Beyond their mathematical and practical applications, obtuse angles also hold significance in art and design.
14.1. Visual Harmony
Artists and designers use obtuse angles to create visual harmony and balance in their compositions. The angles can guide the viewer’s eye and create a sense of flow and movement. By strategically incorporating obtuse angles, artists can evoke specific emotions and enhance the overall impact of their work.
14.2. Perspective and Depth
Obtuse angles can be used to create a sense of perspective and depth in paintings and drawings. By varying the angles and their placement, artists can simulate three-dimensional space on a two-dimensional surface. This technique is particularly useful in landscape and architectural drawings.
14.3. Modern Art and Design
In modern art and design, obtuse angles are often used to create bold and unconventional forms. Designers may use these angles to challenge traditional aesthetics and create pieces that are both visually striking and thought-provoking. This approach is common in contemporary sculpture and architectural design.
15. How Obtuse Angles Affect Navigation and Mapping
Obtuse angles play a crucial role in navigation and mapping, affecting everything from ship routes to the accuracy of maps.
15.1. Calculating Bearings
Navigators use obtuse angles to calculate bearings and determine the direction of travel. Accurate angle measurements are essential for plotting courses and avoiding obstacles. Whether at sea or in the air, understanding obtuse angles can significantly improve navigation accuracy.
15.2. Map Projections
Map projections, which transform the Earth’s curved surface onto a flat plane, often involve the use of obtuse angles. Cartographers must account for these angles to minimize distortion and ensure the map accurately represents the real world. The choice of map projection depends on the intended use and the area being mapped.
15.3. GPS Technology
GPS technology relies on precise angle measurements to determine a user’s location. Satellites transmit signals that are used to calculate the angles between the receiver and the satellites. These angles are then used to triangulate the user’s position with a high degree of accuracy.
16. Advanced Trigonometry and Obtuse Angles
Advanced trigonometry delves deeper into the properties and applications of obtuse angles, providing a more comprehensive understanding of their behavior.
16.1. The Sine Rule
The sine rule relates the sides of a triangle to the sines of its angles. It is particularly useful for solving triangles when you know one side and two angles, or two sides and one angle opposite one of them. The sine rule can be applied to both acute and obtuse triangles.
16.2. The Cosine Rule
The cosine rule relates the sides of a triangle to the cosine of one of its angles. It is used to find the length of a side if you know the other two sides and the included angle, or to find an angle if you know all three sides. The cosine rule is essential for solving triangles that are not right-angled.
16.3. Applications in Physics
In physics, obtuse angles are used in vector analysis to resolve forces and velocities into components. This is crucial for understanding motion and equilibrium in complex systems. For example, when analyzing the forces acting on an object on an inclined plane, obtuse angles are used to determine the components of the gravitational force.
17. The Psychological Impact of Obtuse Angles in Design
Obtuse angles, beyond their mathematical properties, have a subtle yet significant impact on human psychology, particularly in design.
17.1. Creating a Sense of Openness
In interior design, obtuse angles can create a sense of openness and spaciousness. By using these angles in the layout of rooms or in the design of furniture, designers can make spaces feel more inviting and less confined. This is particularly useful in small apartments or offices.
17.2. Comfort and Relaxation
The angle of a chair’s backrest or the slope of a bed can influence comfort and relaxation. Obtuse angles often contribute to a more ergonomic and comfortable design, allowing people to relax more easily. This is why many ergonomic chairs and mattresses incorporate obtuse angles in their design.
17.3. Visual Appeal
Obtuse angles can add visual interest to designs. By incorporating these angles, designers can create pieces that are both functional and aesthetically pleasing. This is especially common in modern architecture and furniture design, where unconventional angles are used to create unique and striking forms.
18. Obtuse Angles in Nature: Natural Occurrences and Biological Adaptations
Obtuse angles are not just a human construct; they appear naturally in various forms and serve crucial functions in the natural world.
18.1. Branching Patterns in Trees
The angles at which branches extend from a tree trunk often approximate obtuse angles. These angles help maximize sunlight capture by reducing overlap among branches. The branching pattern is a crucial adaptation that allows trees to thrive in competitive environments.
18.2. Angles in Animal Morphology
Certain animals exhibit obtuse angles in their body structure that aid in movement and balance. For example, the angle between a bird’s wing and body during flight can be obtuse, optimizing lift and reducing drag. Similarly, the angles in a reptile’s limbs can provide stability and facilitate movement across diverse terrains.
18.3. Geological Formations
Geological formations, such as rock strata and mountain peaks, can display obtuse angles formed over millions of years by erosion and tectonic forces. These angles often define the landscape’s character and influence drainage patterns.
19. Interactive Learning Resources for Mastering Obtuse Angles
To further enhance your understanding of obtuse angles, several interactive learning resources are available.
19.1. Online Angle Calculators
Online angle calculators allow you to input known angles and quickly determine unknown angles in geometric shapes. These tools are excellent for verifying your manual calculations and exploring different scenarios.
19.2. Geometry Simulation Software
Geometry simulation software enables you to create and manipulate geometric shapes, including triangles and quadrilaterals with obtuse angles. These simulations provide a hands-on approach to learning, allowing you to observe how changes in angle measurements affect the shape’s properties.
19.3. Educational Apps
Educational apps offer interactive lessons, quizzes, and games focused on geometry and trigonometry. Many of these apps include specific modules on obtuse angles, complete with visual aids and practice exercises.
20. Career Paths That Utilize Knowledge of Obtuse Angles
A strong understanding of obtuse angles is valuable in various career paths, particularly those involving design, construction, and engineering.
20.1. Architects
Architects use obtuse angles to design buildings that are both aesthetically pleasing and structurally sound. They must consider angles when planning roof structures, wall alignments, and interior layouts. A solid grasp of geometry is essential for creating functional and visually appealing designs.
20.2. Civil Engineers
Civil engineers apply their knowledge of obtuse angles to design bridges, roads, and other infrastructure projects. They must accurately calculate angles to ensure structures are stable and can withstand various loads. An understanding of trigonometry and vector analysis is crucial for success in this field.
20.3. Interior Designers
Interior designers use obtuse angles to create comfortable and visually harmonious spaces. They consider angles when selecting furniture, arranging layouts, and designing custom features. An understanding of spatial relationships and visual balance is essential for creating appealing and functional interiors.
Unlock the mysteries of obtuse angles with WHAT.EDU.VN! Do you have burning questions about obtuse angles or other geometrical concepts? Don’t hesitate! Visit WHAT.EDU.VN today to ask your questions and receive fast, free answers from our community of experts. Whether you’re a student, a professional, or simply curious, we’re here to help you understand the world around you. Contact us at 888 Question City Plaza, Seattle, WA 98101, United States. Whatsapp: +1 (206) 555-7890 or visit our website what.edu.vn.