What Is Arcsin? Definition, Formula, Graph, and Examples

Arcsine, often confusing, but not anymore! At WHAT.EDU.VN, we unravel the mysteries of “What Is Arcsin” with crystal-clear explanations, formulas, graphs, and real-world examples. We provide solutions for students seeking answers, professionals expanding their knowledge, and the simply curious. Discover the inverse sine function and unlock its secrets with us. Explore trigonometric inverses with WHAT.EDU.VN!

1. Unveiling the Arcsin: The Inverse Sine Explained

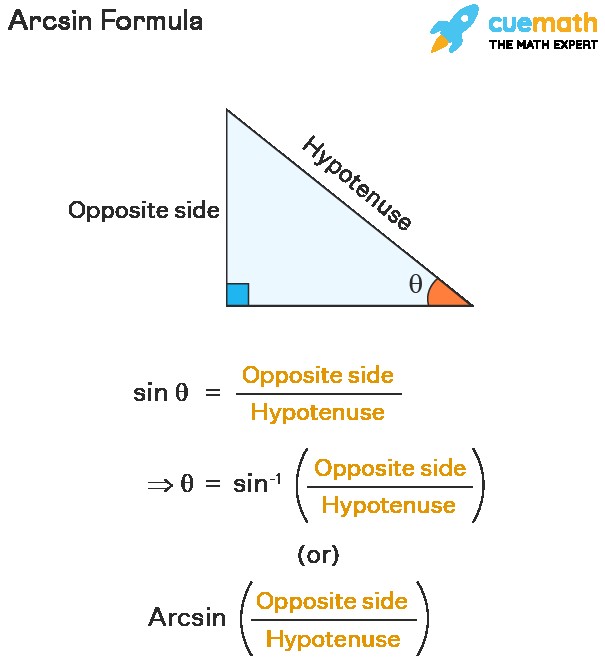
Arcsine, denoted as arcsin(x) or sin^-1(x), is the inverse trigonometric function of the sine function. Simply put, it answers the question: “What angle has a sine of x?” It’s crucial to understand that sin^-1(x) does not mean 1/sin(x) (which is csc(x), the cosecant). Arcsin is your key to unlocking the angle when you know the ratio of the opposite side to the hypotenuse in a right triangle.

1.1. Arcsin in Action: A Quick Example

Imagine you have a right triangle where the ratio of the opposite side to the hypotenuse is 0.5. What angle corresponds to this ratio? That’s where arcsin comes in!

arcsin(0.5) = π/6 radians or 30 degrees.

This means that an angle of 30 degrees has a sine of 0.5.

1.2. The Family of Inverse Trigonometric Functions

Arcsin is just one member of the family of inverse trigonometric functions. Here are the six main players:

arcsin(x): Inverse sine
arccos(x): Inverse cosine
arctan(x): Inverse tangent
arccsc(x): Inverse cosecant
arcsec(x): Inverse secant
arccot(x): Inverse cotangent

Each of these functions “undoes” its corresponding trigonometric function.

2. Deconstructing the Arcsin Formula: Finding the Angle

The arcsin formula directly relates the ratio of the opposite side to the hypotenuse in a right triangle to the angle itself.

2.1. The Core Formula

θ = arcsin(Opposite / Hypotenuse)

Where:

θ is the angle in radians or degrees.
Opposite is the length of the side opposite to the angle.
Hypotenuse is the length of the hypotenuse (the longest side).

2.2. Law of Sines and Arcsin: A Powerful Combination

The Law of Sines provides another avenue for calculating angles using arcsin, especially when dealing with non-right triangles. The Law of Sines states:

a / sin(A) = b / sin(B) = c / sin(C)

Where:

a, b, c are the sides of the triangle.
A, B, C are the angles opposite those sides.

Rearranging and applying arcsin:

A = arcsin( (a / b) * sin(B) )

This formula allows you to find angle A if you know sides a and b, and angle B.

2.3. Step-by-Step Example Using the Law of Sines

Let’s say you have a triangle where:

a = 5
b = 7
B = 45 degrees (π/4 radians)

To find angle A:

sin(B) = sin(45°) = √2 / 2
(a / b) sin(B) = (5 / 7) (√2 / 2) ≈ 0.505
A = arcsin(0.505) ≈ 0.529 radians or 30.3 degrees

Therefore, angle A is approximately 30.3 degrees.

3. Visualizing Arcsin: The Graph Unveiled

The graph of arcsin(x) provides a visual representation of the function’s behavior and its domain and range.

3.1. Key Points for Plotting

Here are some crucial points to accurately plot the arcsin(x) graph:

arcsin(-1) = -π/2 ≈ -1.571
arcsin(-√3/2) = -π/3 ≈ -1.047
arcsin(-√2/2) = -π/4 ≈ -0.785
arcsin(-1/2) = -π/6 ≈ -0.524
arcsin(0) = 0
arcsin(1/2) = π/6 ≈ 0.524
arcsin(√2/2) = π/4 ≈ 0.785
arcsin(√3/2) = π/3 ≈ 1.047
arcsin(1) = π/2 ≈ 1.571

3.2. The Arcsin Graph: Shape and Characteristics

The arcsin graph has the following characteristics:

It’s a continuous curve.
It increases from left to right.
It’s symmetric about the origin (odd function).
It’s defined only between x = -1 and x = 1.
Its y-values (range) lie between -π/2 and π/2.

4. Domain and Range: Defining the Boundaries of Arcsin

Understanding the domain and range is crucial for working with arcsin effectively.

4.1. Why Restrictions Are Necessary

The sine function, sin(x), repeats its values infinitely. To define a proper inverse function, we need to restrict the domain of sin(x) to an interval where it’s one-to-one (bijective). This ensures that each input has only one output, and vice versa.

4.2. The Principal Value Branch

The most common restriction for sin(x) is the interval [-π/2, π/2]. This is called the principal value branch. It’s on this interval that we define arcsin(x).

4.3. Domain of Arcsin

The domain of arcsin(x) is [-1, 1]. This means arcsin(x) is only defined for input values between -1 and 1, inclusive. This is because the sine function only produces values in this range.

4.4. Range of Arcsin

The range of arcsin(x) is [-π/2, π/2]. This means the output of arcsin(x) will always be an angle between -π/2 and π/2 radians (or -90 and 90 degrees).

5. Mastering Arcsin: Essential Identities

Arcsine identities are powerful tools for simplifying expressions and solving trigonometric equations.

5.1. Fundamental Identities

sin(arcsin(x)) = x, for x ∈ [-1, 1]
arcsin(sin(x)) = x, for x ∈ [-π/2, π/2]

5.2. Reciprocal Identity

arcsin(1/x) = arccsc(x), for |x| ≥ 1

5.3. Odd Function Identity

arcsin(-x) = -arcsin(x), for x ∈ [-1, 1]

5.4. Complementary Angle Identity

arcsin(x) + arccos(x) = π/2, for x ∈ [-1, 1]

5.5. Double Angle Identities

2 arcsin(x) = arcsin(2x√(1 – x²)), for -1/√2 ≤ x ≤ 1/√2
2 arccos(x) = arcsin(2x√(1 – x²)), for 1/√2 ≤ x ≤ 1

5.6. Sum and Difference Identities

arcsin(x) + arcsin(y) = arcsin(x√(1 – y²) + y√(1 – x²))
arcsin(x) – arcsin(y) = arcsin(x√(1 – y²) – y√(1 – x²))

5.7. Applying Identities: An Example

Let’s simplify the expression: sin(2 arcsin(x))

Using the double angle identity for sine: sin(2θ) = 2sin(θ)cos(θ)

Let θ = arcsin(x), then sin(θ) = x. We need to find cos(θ).

Using the Pythagorean identity: sin²(θ) + cos²(θ) = 1

cos²(θ) = 1 – sin²(θ) = 1 – x²

cos(θ) = √(1 – x²)

Therefore, sin(2 arcsin(x)) = 2 x √(1 – x²)

6. Common Arcsin Questions Answered

Let’s address some frequently asked questions about arcsin.

6.1. What is Arcsin in Trigonometry?

Arcsin is the inverse trigonometric function of sine. It finds the angle whose sine is a given value. It’s one of the six inverse trigonometric functions, alongside arccos, arctan, arccsc, arcsec, and arccot. Remember, arcsin(x) is not the same as 1/sin(x).

6.2. What is the Arcsin Formula?

The basic formula is: θ = arcsin(Opposite / Hypotenuse) in a right-angled triangle. You can also use the Law of Sines to derive variations for non-right triangles.

6.3. What is the Derivative of Arcsin x?

The derivative of arcsin(x) is: d/dx(arcsin(x)) = 1 / √(1 – x²)

6.4. How to Integrate Arcsin?

The integral of arcsin(x) is: ∫arcsin(x) dx = x * arcsin(x) + √(1 – x²) + C, where C is the constant of integration. This is typically solved using integration by parts.

6.5. What is the Domain and Range of Arcsin?

Domain: [-1, 1]
Range: [-π/2, π/2]

These restrictions are essential to ensure that arcsin is a well-defined inverse function.

6.6. How to Plot the Arcsin Graph?

Calculate arcsin(x) for various values of x between -1 and 1.
Plot these (x, arcsin(x)) points on a graph.
Connect the points with a smooth curve. Remember the key points and the general shape.

6.7. Is Arcsin the Inverse of Sin?

Yes, arcsin is the inverse function of sin, but only when sin is restricted to the domain [-π/2, π/2].

6.8. What is the Difference between Sin and Arcsin?

Sine (sin) takes an angle as input and returns a ratio (between -1 and 1). Arcsin takes a ratio (between -1 and 1) as input and returns an angle (between -π/2 and π/2). They “undo” each other.

6.9. Why Arcsin (-2) is Not Defined?

Arcsine of -2 is undefined because the domain of arcsin is [-1, 1]. -2 falls outside this domain. The sine function can never output a value of -2.

6.10. What are the Identities of Arcsin?

We’ve listed several essential identities above, including fundamental, reciprocal, odd function, complementary angle, double angle, and sum/difference identities. These are valuable for simplification and problem-solving.

6.11. What is Arcsin of Sin?

arcsin(sin(x)) = x only if x is within the interval [-π/2, π/2]. If x is outside this interval, you need to find an equivalent angle within the interval that has the same sine value.

7. Ready to Dive Deeper? Ask Your Questions at WHAT.EDU.VN!

Do you still have questions about arcsin, inverse trigonometric functions, or any other math topic? Don’t struggle in silence!

At WHAT.EDU.VN, we provide a free and easy-to-use platform where you can ask any question and receive prompt, accurate answers from knowledgeable experts. We understand the challenges students, professionals, and curious minds face when seeking information. That’s why we’ve created a supportive community where you can get the help you need, when you need it.

7.1. Why Choose WHAT.EDU.VN?

It’s Free: Ask unlimited questions without any subscription fees or hidden charges.
Fast & Accurate Answers: Get reliable responses from experienced individuals.
Easy to Use: Our platform is designed for simplicity and ease of navigation.
Community Support: Connect with other learners and experts to share knowledge.
Any Question Welcome: From basic concepts to complex problems, we’re here to help.

7.2. Take Action Now!

Don’t let confusion hold you back. Visit WHAT.EDU.VN today and submit your question! Our team is ready to provide you with the clear, concise answers you need to succeed.

Contact Information:

Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: WHAT.EDU.VN

We look forward to helping you unlock the power of knowledge at what.edu.vn!