What Is Arctan? The Inverse Tangent Function Explained

Arctan, or the inverse tangent function, is a fundamental concept in trigonometry and calculus. If you’re looking for a clear understanding of arctan, its applications, and how it works, WHAT.EDU.VN is here to help. Discover everything you need to know about arctan, inverse trig functions, and trigonometric ratios in this comprehensive guide. Let’s explore inverse functions, angle values, and real numbers.

1. What Is Arctan?

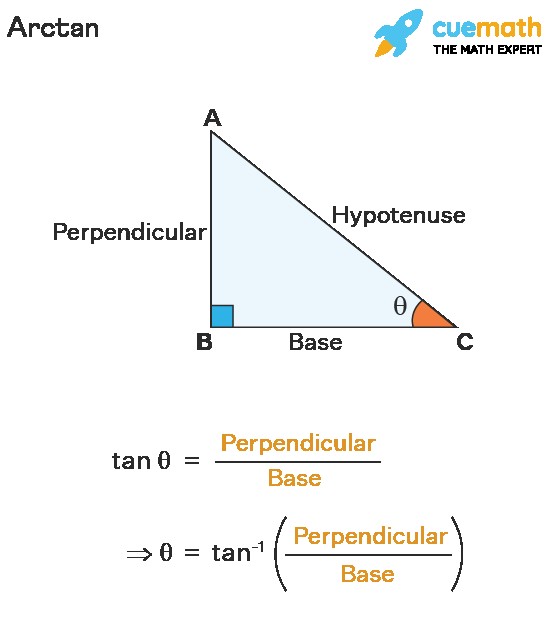
Arctan, short for “arc tangent,” is the inverse function of the tangent function. Simply put, it answers the question: “What angle has this tangent value?” While the tangent function (tan) calculates the ratio of the opposite side to the adjacent side in a right triangle given an angle, the arctan function does the opposite. It takes the ratio and returns the corresponding angle.

Understanding the Basics: In a right-angled triangle, tan(θ) = Opposite / Adjacent. Conversely, arctan(Opposite / Adjacent) = θ.
Notation: Arctan is commonly written as arctan(x) or tan⁻¹(x). It’s crucial to remember that tan⁻¹(x) does not mean 1 / tan(x).
Practical Application: Arctan is widely used in fields like navigation, physics, and engineering to determine angles based on known ratios.
Example: If tan(45°) = 1, then arctan(1) = 45° (or π/4 radians).

2. Why Is Arctan Important?

Arctan is essential for several reasons:

Solving for Angles: It allows us to find unknown angles in right triangles when we know the ratio of the opposite and adjacent sides.
Inverses of Trigonometric Functions: It’s a core member of the inverse trigonometric function family, including arcsin (inverse sine) and arccos (inverse cosine).
Applications in Calculus: Arctan appears in various integration and differentiation problems.
Real-World Problem Solving: Engineers and scientists use arctan to calculate angles in various applications, from trajectory calculations to electrical circuit analysis.

3. The Arctan Formula

The fundamental formula for arctan is:

arctan(Opposite / Adjacent) = θ

Where:

θ is the angle you’re trying to find.
Opposite is the length of the side opposite the angle in a right triangle.
Adjacent is the length of the side adjacent to the angle in a right triangle.

This formula allows you to calculate the angle in radians or degrees, depending on the calculator or software you’re using.

4. Arctan Identities

Arctan identities are equations that simplify or transform expressions involving the arctan function. Here are some common and useful identities:

arctan(-x) = -arctan(x): This shows that arctan is an odd function, meaning it is symmetrical about the origin.
tan(arctan(x)) = x: This identity illustrates the inverse relationship between tangent and arctangent.
arctan(tan(x)) = x for x ∈ (-π/2, π/2): This holds true only within the principal range of arctan.
arctan(1/x) = π/2 – arctan(x) = arccot(x) if x > 0, or arctan(1/x) = -π/2 – arctan(x) = arccot(x) – π if x < 0: This relates arctan to arccotangent.
sin(arctan(x)) = x / √(1 + x²): This expresses the sine of arctan in terms of x.
cos(arctan(x)) = 1 / √(1 + x²): This expresses the cosine of arctan in terms of x.
arctan(x) = 2arctan(x / (1 + √(1 + x²))): A more complex identity used in specific situations.

5. Special Arctan Values

It’s helpful to memorize arctan values for common ratios:

Ratio (x)	Arctan(x) (Degrees)	Arctan(x) (Radians)
0	0°	0
1/√3	30°	π/6
1	45°	π/4
√3	60°	π/3
∞	90°	π/2

6. Domain and Range of Arctan

Domain: The domain of arctan(x) is all real numbers (-∞ to ∞). This means you can input any real number into the arctan function.
Range: The range of arctan(x) is (-π/2, π/2) in radians, or (-90°, 90°) in degrees. This is known as the principal range, and it ensures that the arctan function has a unique output for each input.

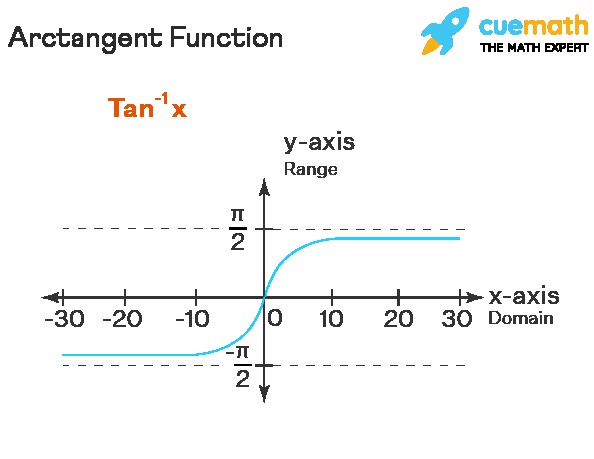
7. Arctan Graph

The graph of y = arctan(x) is a curve that passes through the origin. It is symmetric about the origin because arctan is an odd function. As x approaches infinity, arctan(x) approaches π/2, and as x approaches negative infinity, arctan(x) approaches -π/2.

8. Properties of the Arctan Function

Odd Function: As mentioned earlier, arctan(-x) = -arctan(x).
Monotonic Increasing: The arctan function is always increasing as x increases.
Bounded: The output of arctan is always between -π/2 and π/2.
Continuous: The arctan function is continuous for all real numbers.

9. Derivative of Arctan

The derivative of arctan(x) is:

d/dx (arctan(x)) = 1 / (1 + x²)

This derivative is used in various calculus problems involving integration and optimization.

10. Integral of Arctan

The integral of arctan(x) is:

∫ arctan(x) dx = x * arctan(x) - 0.5 * ln(1 + x²) + C

Where C is the constant of integration. This integral is usually solved using integration by parts.

11. How to Calculate Arctan

Calculators: Most scientific calculators have an arctan or tan⁻¹ button. Make sure your calculator is in the correct mode (degrees or radians) before performing the calculation.
Software: Programming languages like Python (using the math.atan() function) and spreadsheets like Excel (using the ATAN() function) can calculate arctan.
Tables: Trigonometric tables provide pre-calculated values for arctan for specific ratios.

12. Arctan vs. Tan

Feature	Tangent (tan)	Arctangent (arctan)
Input	Angle	Ratio of opposite to adjacent sides
Output	Ratio of opposite to adjacent sides	Angle
Domain	All real numbers except odd multiples of π/2	All real numbers
Range	All real numbers	(-π/2, π/2)
Function Type	Trigonometric Function	Inverse Trigonometric Function

13. Common Mistakes to Avoid

Confusing tan⁻¹(x) with 1 / tan(x): Remember, tan⁻¹(x) is the inverse tangent, while 1 / tan(x) is the cotangent.
Incorrect Calculator Mode: Ensure your calculator is in the correct mode (degrees or radians) to get the correct angle.
Forgetting the Principal Range: The arctan function always returns an angle in the range (-π/2, π/2). If you need an angle outside this range, you may need to add or subtract multiples of π.

14. Real-World Applications of Arctan

Navigation: Calculating headings and bearings.
Physics: Determining angles of projectile motion.
Engineering: Designing structures and electrical circuits.
Computer Graphics: Calculating viewing angles and rotations.
Robotics: Determining joint angles for robot arms.

15. Examples of Arctan in Action

Example 1: A ladder leans against a wall, with the base 5 feet away from the wall and the top 12 feet up the wall. What is the angle of elevation of the ladder?

Solution: arctan(12/5) ≈ 67.38°
Example 2: A drone flies 50 meters horizontally and rises 20 meters vertically. What is the angle of ascent?

Solution: arctan(20/50) ≈ 21.80°

16. Advanced Concepts Related to Arctan

Complex Numbers: Arctan can be extended to complex numbers, leading to complex analysis applications.
Taylor Series: The arctan function has a Taylor series expansion:

arctan(x) = x - x³/3 + x⁵/5 - x⁷/7 + ...
Hyperbolic Functions: Arctan is related to inverse hyperbolic functions like atanh(x).

17. Arctan and Right Triangle Trigonometry

In right triangle trigonometry, arctan is used to find an angle when the opposite and adjacent sides are known. The formula is:

θ = arctan(opposite / adjacent)

For example, if the opposite side is 3 and the adjacent side is 4:

θ = arctan(3 / 4) ≈ 36.87°

18. Tips for Mastering Arctan

Practice: Work through various example problems to solidify your understanding.
Visualization: Draw right triangles and visualize the relationship between the sides and angles.
Memorization: Memorize common arctan values and identities.
Use Technology: Utilize calculators and software to perform complex arctan calculations.

19. Arctan Table: Quick Reference Guide

Value (x)	arctan(x) (Degrees)	arctan(x) (Radians)
-∞	-90°	-π/2
-1	-45°	-π/4
-√3/3	-30°	-π/6
0	0°	0
√3/3	30°	π/6
1	45°	π/4
√3	60°	π/3
∞	90°	π/2

This table provides quick references for common arctan values, making calculations faster and more efficient.

20. Trigonometry and Calculus: Arctan’s Role

Arctan serves as a vital link between trigonometry and calculus. Its derivative and integral are frequently encountered in calculus problems, particularly in integration techniques and differential equations. Understanding arctan enables efficient problem-solving in both theoretical and applied mathematical contexts.

21. Common Mistakes to Avoid When Using Arctan

Forgetting the Domain Restrictions: Be mindful of the principal range (-π/2, π/2).
Misinterpreting Notation: tan⁻¹(x) is not the same as 1 / tan(x).
Calculator Errors: Double-check your calculator mode (degrees or radians).

22. Arctan in Different Programming Languages

Different programming languages provide functions to calculate arctan. Here are some examples:

Python:

import math
angle_radians = math.atan(1) # Returns π/4
angle_degrees = math.degrees(angle_radians) # Converts to degrees

JavaScript:

let angle_radians = Math.atan(1); // Returns π/4
let angle_degrees = angle_radians * 180 / Math.PI; // Converts to degrees

C++:

#include <iostream>
#include <cmath>

int main() {
    double angle_radians = std::atan(1); // Returns π/4
    double angle_degrees = angle_radians * 180 / M_PI; // Converts to degrees
    std::cout << angle_degrees << std::endl;
    return 0;
}

23. Practical Exercises to Improve Arctan Skills

Ladder Problem: A ladder 10 feet long leans against a wall, with its base 6 feet from the wall. Find the angle the ladder makes with the ground.
Drone Ascent: A drone flies 80 meters horizontally and ascends 30 meters vertically. Determine the drone’s angle of ascent.
Ramp Design: A ramp needs to have a height of 2 meters and a horizontal distance of 5 meters. Calculate the angle of elevation for the ramp.

24. What If You’re Still Struggling With Arctan?

If you find arctan challenging, don’t worry. Many resources can help:

Online Tutorials: Websites like Khan Academy offer detailed lessons and practice problems.
Tutoring: Consider hiring a math tutor for personalized instruction.
Textbooks: Refer to trigonometry and calculus textbooks for in-depth explanations.
WHAT.EDU.VN: Visit WHAT.EDU.VN to ask questions and get free answers from experts.

25. Advanced Arctan Identities and Formulas

For more advanced use cases, here are some additional identities:

arctan(x) + arctan(y) = arctan((x + y) / (1 – xy)): This is useful for combining two arctan terms.
arctan(x) – arctan(y) = arctan((x – y) / (1 + xy)): This helps in subtracting arctan terms.
*2 arctan(x) = arctan((2x) / (1 – x²))**: Useful for doubling an arctan value.

26. The Role of Arctan in Data Science

In data science, arctan is used in various contexts, such as:

Feature Engineering: Creating new features from existing ones.
Angle Calculation: Finding angles between vectors.
Normalization: Transforming data to fit a specific range.

27. How Arctan Bridges Trigonometry and Geometry

Arctan elegantly connects trigonometry and geometry by providing a means to calculate angles within geometric shapes. This function is indispensable in architectural designs, land surveying, and other practical fields where angular measurements are crucial for precision and accuracy.

28. Complex Numbers and Arctan

The relationship between complex numbers and arctan is an advanced topic in complex analysis. The arctan function can be extended to complex arguments, allowing us to find angles in the complex plane.

29. Trigonometric Equations Involving Arctan

Solving trigonometric equations involving arctan requires careful consideration of the domain and range. It’s essential to verify solutions to ensure they are valid.

30. History and Evolution of Arctan

The concept of arctan dates back to ancient civilizations, with early mathematicians exploring inverse trigonometric functions. Over time, these functions were formalized and found widespread applications in various fields.

31. Frequently Asked Questions (FAQs) About Arctan

What is the arctan of infinity? The arctan of infinity is π/2 radians (90 degrees).
Is arctan a periodic function? No, arctan is not a periodic function. It has a bounded range between -π/2 and π/2.
How is arctan used in computer graphics? Arctan is used to calculate viewing angles, rotations, and other transformations in 3D graphics.
What is the relationship between arctan and arccot? arctan(x) + arccot(x) = π/2
Why is the range of arctan restricted? The range is restricted to ensure that the arctan function has a unique output for each input.

32. Arctan and Its Relevance in Modern Technology

Modern technology relies heavily on arctan for applications like GPS, robotics, and augmented reality. Accurate angle calculations are essential for these technologies to function effectively.

33. How to Memorize Arctan Values Easily

A helpful mnemonic for remembering common arctan values is to associate them with special right triangles:

30-60-90 triangle: arctan(1/√3) = 30°, arctan(√3) = 60°
45-45-90 triangle: arctan(1) = 45°

34. The Significance of Understanding Arctan for STEM Students

For students pursuing STEM fields, a solid understanding of arctan is crucial. It forms the basis for advanced concepts in mathematics, physics, and engineering.

35. How to Use Arctan in Architectural Designs

Architects use arctan to calculate roof angles, slope gradients, and other geometric parameters. Accurate angle calculations are essential for structural integrity and aesthetic appeal.

36. Using Arctan in Game Development

Game developers use arctan to calculate angles for character movement, projectile trajectories, and camera perspectives. Accurate angle calculations are essential for realistic and engaging gameplay.

37. Arctan for Land Surveying and Mapping

Land surveyors use arctan to determine angles and distances in terrain mapping. These calculations are essential for creating accurate maps and boundary demarcations.

38. Solving Trigonometric Equations with Arctan

To solve trigonometric equations with arctan:

Isolate the arctan term.
Take the tangent of both sides.
Solve for the variable.
Check for extraneous solutions.

39. Arctan and Its Influence on Electrical Engineering

In electrical engineering, arctan is used to analyze AC circuits, calculate phase angles, and design filters. Accurate angle calculations are essential for circuit performance and stability.

40. Simplifying Complex Expressions Using Arctan Identities

Arctan identities can simplify complex expressions, making calculations easier and more efficient. Memorizing these identities is highly beneficial.

41. How to Explain Arctan to a Child

Explain arctan as the reverse of finding how steep a slide is. If you know how far the slide goes across and how high it is, arctan tells you the angle of the slide.

42. Where to Find More Help with Arctan

For more help with arctan, visit online math forums, consult math textbooks, or seek assistance from a math tutor.

43. Arctan in Everyday Life

Although not always obvious, arctan has applications in everyday life, such as:

Adjusting the angle of a sunshade.
Calculating the incline of a ramp.
Using GPS for navigation.

44. Arctan and the Concept of Angular Velocity

Arctan is used to calculate the angular velocity of objects in motion, which is essential in physics and engineering.

45. Benefits of Using Online Arctan Calculators

Online arctan calculators provide quick and accurate results, saving time and effort. They are especially useful for complex calculations.

46. Tips for Improving Your Trigonometry Skills

Practice regularly: Consistent practice is key to mastering trigonometry.
Use visual aids: Diagrams and graphs can help you understand concepts better.
Solve problems: Work through various problems to apply your knowledge.
Seek help when needed: Don’t hesitate to ask for assistance if you’re struggling.

47. Arctan and Other Inverse Trigonometric Functions

Arctan is one of several inverse trigonometric functions, including arcsin and arccos. Each function has its specific applications and properties.

48. Integrating Trigonometric Functions with Arctan

Arctan can be used to integrate complex trigonometric functions, often simplifying the integration process.

49. Mastering Arctan: A Lifelong Skill

Mastering arctan provides a valuable skill set applicable in various fields, from mathematics to engineering. Continuous learning and practice will enhance your proficiency.

50. Final Thoughts on Arctan

Arctan is an essential concept in trigonometry and calculus with numerous applications in various fields. Whether you’re a student, engineer, or scientist, understanding arctan will enhance your problem-solving skills and broaden your mathematical knowledge.

Do you still have questions about arctan or other mathematical concepts? Don’t hesitate to ask! At WHAT.EDU.VN, we provide a platform for you to ask any question and receive free answers from knowledgeable community members.

Get Your Questions Answered for Free on WHAT.EDU.VN

Are you struggling with arctan or any other topic? Do you need a quick and reliable answer? Look no further! WHAT.EDU.VN offers a free platform where you can ask any question and receive answers from experts and community members.

Why choose WHAT.EDU.VN?

Free: Ask as many questions as you like without any cost.
Fast: Get answers quickly from a responsive community.
Accurate: Receive reliable information from knowledgeable individuals.
Easy to use: Our platform is simple and intuitive.
Comprehensive: Get help with any subject, not just arctan!

Don’t let your questions go unanswered. Visit WHAT.EDU.VN today and get the help you need to succeed.

Contact Information:

Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: what.edu.vn

We’re here to help you learn and grow. Ask your question now!

What Is Arctan? The Inverse Tangent Function Explained

Get Your Questions Answered for Free on WHAT.EDU.VN

Comments

Leave a Reply Cancel reply