What Is Area In Math? Discover the definition, formulas, real-world applications, and more at WHAT.EDU.VN. Unlock your mathematical potential with our free resources and expert guidance.
Are you struggling to understand the concept of area in math? Do you need a clear explanation of area formulas and their applications? Look no further. At WHAT.EDU.VN, we provide free, accessible, and comprehensive resources to help you master mathematical concepts like area. Learn about surface area, unit squares, and more.
Here’s what we’ll cover in this guide:
- Area definition and its significance in mathematics.
- Different methods to calculate area, including unit squares.
- Area formulas for various geometric shapes.
- Real-life applications of area.
- The difference between area, perimeter, and volume.
- Answers to frequently asked questions about area.
If you still have questions after reading, don’t hesitate to ask them on WHAT.EDU.VN! Our community is here to help.
1. Defining Area: The Space Within
In mathematics, area refers to the amount of two-dimensional space enclosed within a boundary. It’s a fundamental concept in geometry and is essential for understanding the size and extent of surfaces. The area provides a way to quantify the size of a flat surface or shape. It is a two-dimensional quantity, meaning it only considers length and width, not depth.
Area is a two-dimensional quantity, measured in square units.
The concept of area is used in many real-world applications, such as:
- Calculating the size of a room.
- Determining the amount of paint needed to cover a wall.
- Measuring the surface of a field or garden.
Understanding area is essential for anyone working with shapes, spaces, or surfaces.
2. The Historical Roots of Area
The concept of area has ancient origins, dating back to civilizations like the Egyptians and Babylonians, who needed to measure land for agriculture and construction. The invention of the wheel was a prime step of translating objects into geometric shapes. In the early days, the interpretation of “area” using a formula for geometric shapes evolved from the experiments conducted by Archimedes.
Early civilizations relied on area calculations for practical purposes.
These early measurements laid the foundation for the development of geometry and mathematical formulas for calculating the area of various shapes. Today, area remains a crucial concept in fields such as:
- Architecture
- Engineering
- Design
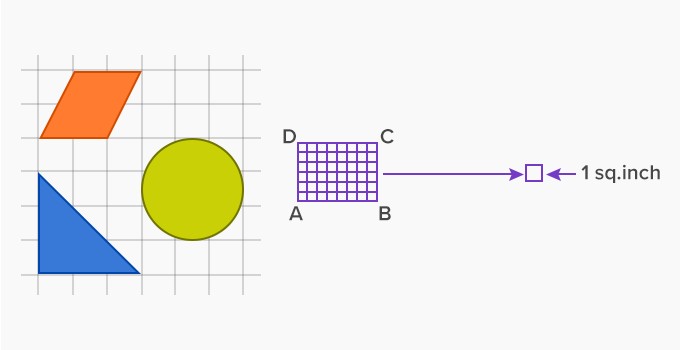
3. Calculating Area Using Unit Squares
One of the simplest ways to understand area is by using unit squares. A unit square is a square with sides of length 1 unit. The area of any shape can be determined by counting the number of unit squares that fit inside it.
Unit squares provide a visual and intuitive way to measure area.
This method is particularly helpful for understanding the concept of area at a basic level. To calculate the area of a shape using unit squares:
- Draw the shape on a grid of unit squares.
- Count the number of full squares inside the shape.
- Count the number of half squares and divide by 2.
- Add the number of full squares and half squares to get the total area.
4. Standard Units of Measurement for Area
Area is measured in square units, reflecting the two-dimensional nature of the concept. Common units of measurement for area include:
- Square centimeters ($cm^2$)
- Square meters ($m^2$)
- Square inches ($in^2$)
- Square feet ($ft^2$)
- Square kilometers ($km^2$)
- Square miles ($mi^2$)
The choice of unit depends on the size of the surface being measured.
It’s important to use consistent units when calculating area to ensure accurate results. When converting between different units of area, remember that:
- 1 $m^2$ = 10,000 $cm^2$
- 1 $ft^2$ = 144 $in^2$
- 1 $km^2$ = 1,000,000 $m^2$
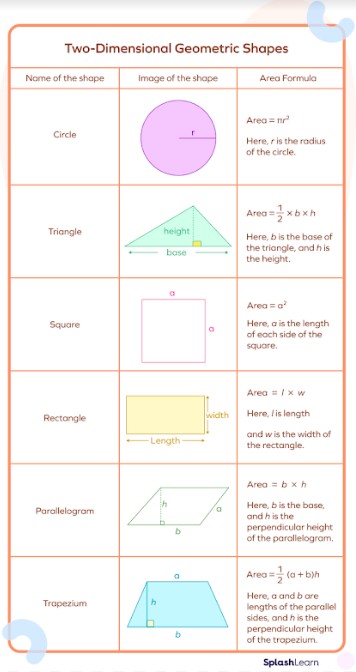
5. Mastering Area Formulas for Basic Shapes
To calculate the area of various shapes, mathematicians have developed specific formulas. These formulas provide a quick and accurate way to determine the area without having to count unit squares. Here are some of the most common area formulas:
- Square: Area = $side^2$
- Rectangle: Area = $length times width$
- Triangle: Area = $frac{1}{2} times base times height$
- Circle: Area = $pi times radius^2$
- Parallelogram: Area = $base times height$
- Trapezoid: Area = $frac{1}{2} times (base1 + base2) times height$
Memorizing these formulas is crucial for solving area-related problems.
6. Area of a Square: The Simplicity of Equal Sides
A square is a quadrilateral with four equal sides and four right angles. The area of a square is simply the square of the length of one of its sides.
The area of a square is easy to calculate due to its equal sides.
Formula:
Area = $side^2$
Example:
If a square has a side length of 5 cm, its area is $5^2 = 25 cm^2$.
7. Area of a Rectangle: Length Times Width
A rectangle is a quadrilateral with four right angles. Its opposite sides are equal in length. The area of a rectangle is the product of its length and width.
The area of a rectangle is a fundamental calculation in geometry.
Formula:
Area = $length times width$
Example:
If a rectangle has a length of 8 cm and a width of 4 cm, its area is $8 times 4 = 32 cm^2$.
8. Area of a Triangle: Half Base Times Height
A triangle is a polygon with three sides. The area of a triangle is half the product of its base and height. The height is the perpendicular distance from the base to the opposite vertex.
Understanding the height is crucial for calculating the area of a triangle.
Formula:
Area = $frac{1}{2} times base times height$
Example:
If a triangle has a base of 10 cm and a height of 6 cm, its area is $frac{1}{2} times 10 times 6 = 30 cm^2$.
9. Area of a Circle: Pi Times Radius Squared
A circle is a set of points equidistant from a central point. The area of a circle is calculated using the formula $pi r^2$, where $pi$ (pi) is approximately 3.14159 and r is the radius of the circle.
The formula for the area of a circle involves the mathematical constant pi.
Formula:
Area = $pi times radius^2$
Example:
If a circle has a radius of 7 cm, its area is $pi times 7^2 approx 3.14159 times 49 approx 153.94 cm^2$.
10. Area of a Parallelogram: Base Times Height
A parallelogram is a quadrilateral with opposite sides parallel. The area of a parallelogram is the product of its base and height. The height is the perpendicular distance between the base and its opposite side.
The height of a parallelogram is the perpendicular distance between its bases.
Formula:
Area = $base times height$
Example:
If a parallelogram has a base of 12 cm and a height of 5 cm, its area is $12 times 5 = 60 cm^2$.
11. Area of a Trapezoid: Half the Sum of Bases Times Height
A trapezoid is a quadrilateral with at least one pair of parallel sides. The area of a trapezoid is half the sum of its parallel sides (bases) multiplied by its height.
A trapezoid has two bases of different lengths.
Formula:
Area = $frac{1}{2} times (base1 + base2) times height$
Example:
If a trapezoid has bases of 8 cm and 10 cm and a height of 4 cm, its area is $frac{1}{2} times (8 + 10) times 4 = 36 cm^2$.
12. Tackling Composite Figures: Combining Shapes
A composite figure is a shape made up of two or more basic shapes. To find the area of a composite figure, you need to:
- Divide the figure into basic shapes.
- Calculate the area of each basic shape.
- Add the areas of all the shapes together.
Composite figures require breaking down into simpler shapes.
Example:
To find the area of a figure made up of a rectangle and a semicircle:
- Calculate the area of the rectangle.
- Calculate the area of the semicircle (half the area of a full circle).
- Add the two areas together.
13. Real-World Applications of Area: Measuring Our Surroundings
The concept of area has numerous practical applications in everyday life. Some examples include:
- Home Improvement: Calculating the amount of flooring, paint, or wallpaper needed for a room.
- Gardening: Determining the amount of fertilizer or mulch needed for a garden bed.
- Construction: Measuring the surface area of a building or structure.
- Design: Calculating the area of fabric needed for a sewing project.
- Real Estate: Assessing the size of a property.
Understanding area is essential for many practical tasks.
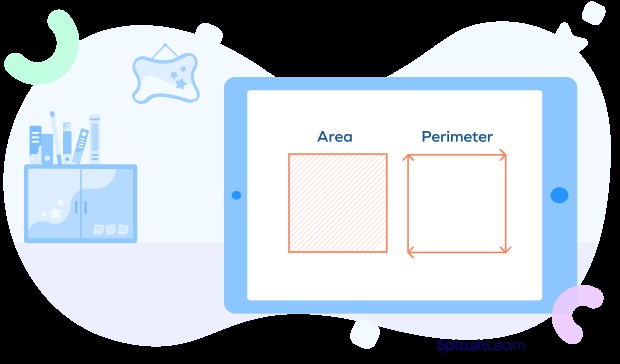
14. Distinguishing Area from Perimeter: Inside vs. Outside
Area and perimeter are related concepts, but they measure different aspects of a shape. Area measures the space inside a shape, while perimeter measures the distance around the shape.
Area and perimeter are both important measurements of a shape.
| Area | Perimeter |
|---|---|
| The space occupied by a closed plane in a two dimensional shape is called area. | Perimeter is the measure of the length of the outer boundary of a closed shape. |
| Area is measured in squared units. | Perimeter is measured in units. |
| Example: Area of tiling the floor | Example: Perimeter of fencing the garden |


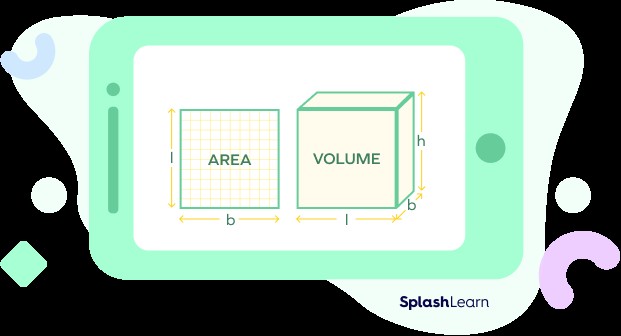

15. Area vs. Volume: Two Dimensions vs. Three Dimensions
Area and volume are both measures of space, but area applies to two-dimensional surfaces, while volume applies to three-dimensional objects.
Area is for flat surfaces, while volume is for solid objects.
| Area | Volume |
|---|---|
| Area is defined for 2-dimensional space. | Volume is defined for 3-dimensional space. |
| The space occupied by a closed plane in a 2-dimensional shape is called area. | The space occupied by a 3-dimensional figure is known as volume. |
| Example: Area of tiling the floor | Example: Volume of the room |
16. Fun Facts About Area: Unveiling Mathematical Curiosities
Here are some fun facts about area:
- The area of the disk was evaluated in the 5th century BCE by Hippocrates of Chios
- Area of triangle is also calculated using Heron’s formula
Area has been a subject of mathematical study for centuries.
17. Solved Examples: Putting Formulas into Practice
Let’s work through some examples to solidify your understanding of area:
-
A circle has a diameter of 20 cm. Find out the area of this circle.
Ans: For the circle, $d = 20$ $cm$.
Radius, $r = frac{d}{2} = 10$ $cm$
Therefore, $A = pi r^{2}$
$= 3.14 times 10 times 10 = 314$ $cm^{2}$
Area of the given circle is $314$ $cm^{2}$.
-
The height of a triangle is 10 cm and the base is 20 cm. What is the area of this triangle?
Ans: Area of the triangle $= frac{1}{2} times b times h$
$= frac{1}{2} times 20 times 10 = 100$ $cm^{2}$
Therefore, the area of the given triangle is $100$ $cm^{2}$.
-
The width of a rectangle is half of its length. The width is measured to be 10 cm. What is the area of the rectangle?
Ans: For the rectangle, $w = 10 cm$ and $l = (10 times 2) = 20$ $cm$.
Area of the rectangle, i.e., $A = l times w$
$A = 20 times 10 = 200$ $cm^{2}$
Therefore, the area of the given rectangle is $200$ $cm^{2}$.
-
What is the area of the following figure?
Solution: Full square $= 1$ square unit
So, 14 full square $= 14$ square units
1 half square $= frac{1}{2}$ square units
5 half squares $= 2.5$ square units
Total area $= 14 + 2.5 = 16.5$ square units.
-
What is the area of a rectangular park whose length and breadth are 30 m and 50 m respectively?
Solution: Given Data:
Length of the park $= 30$ m
Breadth of the park $= 50$ m
Use the area formula.
Area of a Rectangle $= text{Length} times text{Breadth}$
$= (30 times 50)$ $m^{2}$
$= 1500$ $m^{2}$
-
What is the area of a circular cricket stadium whose radius is 200 m?
Solution: Given data:
Radius of the cricket stadium $= 200$ m
Use the area formula.
Area of a Circle $= pi r^{2}$
$= pi times 200 m times 200 m$
$= 40000 pi$ $m^{2}$
-
What is the area of a square paddy field if each of its sides measures 10 units?
Solution: Given data:
Length of the side $= 10$ units
Use the area formula.
Area of the square paddy field $= 10 times 10$
$= 100$ square units
These examples demonstrate how to apply area formulas in different scenarios.
18. Practice Problems: Test Your Knowledge
Test your understanding of area with these practice problems:
Area
Attend this Quiz & Test your knowledge.
1
The side of a square is 7 cm. What is the area of this square?
20 cm$^{2}$
30 cm$^{2}$
40 cm$^{2}$
49 cm$^{2}$
CorrectIncorrect
Correct answer is: 49 cm$^{2}$Area of the square = side $times$ side $A = 7 times 7 = 49$ $cm^{2}$
2
The height of a triangle is 25 cm and the base is 50 cm. What is the area of the triangle?
600 cm$^{2}$
625 cm$^{2}$
650 cm$^{2}$
700 cm$^{2}$
CorrectIncorrect
Correct answer is: 625 cm$^{2}$Area of the triangle $= frac{1}{2} times b times h = frac{1}{2} times 50 times 25 = 625$ $cm^{2}$
3
What is the area of a circle that has a radius of 4 cm?
$40$ $cm^{2}$
$16$ $cm^{2}$
$60.27$ $cm^{2}$
$50.27$ $cm^{2}$
CorrectIncorrect
Correct answer is: $50.27$ $cm^{2}$Area of the circle $= pi r^{2} =3.14 times 4 times 4 = 50.27$ $cm^{2}$
4
The base of a parallelogram is 50 cm and the perpendicular height is 20 cm. What is the area of this parallelogram?
$400$ $cm^{2}$
$500$ $cm^{2}$
$750$ $cm^{2}$
$1000$ $cm^{2}$
CorrectIncorrect
Correct answer is: $1000$ $cm^{2}$Area of the parallelogram $= b times h = 50 times 20 = 1000$ $cm^{2}$.
5
What is the area of a square whose perimeter is 28 m?
$21$ $m^{2}$
$42$ $m^{2}$
$49$ $m^{2}$
$47$ $m^{2}$
CorrectIncorrect
Correct answer is: $49$ $m^{2}$Perimeter of square $= 28$ m Let side of square be ‘s’ m $4 times s = 28$ $Rightarrow s = 7$ So, side of square $= 7$ m Area of square $= s times s = 7 times 7 = 49$ $m^{2}$
6
What is the area of a circle whose radius is 10 cm?
$100pi$ $m^{2}$
$300pi$ $m^{2}$
$400pi$ $m^{2}$
$500pi$ $m^{2}$
CorrectIncorrect
Correct answer is: $100pi$ $m^{2}$Area of circle $= pi r^{2} = pi times 10 times 10 = 100pi$ $m^{2}$
7
The area of a rectangular pool is 500 sq. ft. If the width of the pool is 20 ft, what is its length?
25 ft
30 ft
50 ft
100 ft
CorrectIncorrect
Correct answer is: 25 ftArea of rectangle $= text{Length} times text{Breadth}$ Length $= frac{Area}{Length} = frac{500}{20} = 25$ ft
8
What is the area of a rectangular park whose length and breadth are 80 m and 100 m respectively?
$1800$ $m^{2}$
$180$ $m^{2}$
$1018$ $m^{2}$
$8000$ $m^{2}$
CorrectIncorrect
Correct answer is: $8000$ $m^{2}$Area of rectangle $= text{Length} times text{breadth} = 80 times 100 = 8000$ $m^{2}$
These problems will help you reinforce your understanding of area calculations.
19. Frequently Asked Questions (FAQs) About Area
Q1: What is the formula for the area of a square?
A: The area of a square is calculated by squaring the length of one of its sides. Area = $side^2$.
Q2: How do you calculate the area of a composite figure?
A: To find the area of a composite figure, divide it into basic shapes, calculate the area of each shape, and then add the areas together.
Q3: What is the difference between area and perimeter?
A: Area measures the space inside a shape, while perimeter measures the distance around the shape.
Q4: What are the units of measurement for area?
A: Area is measured in square units, such as square centimeters ($cm^2$), square meters ($m^2$), square inches ($in^2$), and square feet ($ft^2$).
Q5: How is the concept of area used in real life?
A: Area is used in various real-life applications, such as home improvement, gardening, construction, design, and real estate.
20. Conclusion: Mastering the Concept of Area
Area is a fundamental concept in mathematics with numerous practical applications. By understanding the definition of area, learning the formulas for calculating the area of various shapes, and practicing with real-world examples, you can master this important mathematical concept.
We hope this comprehensive guide has helped you understand what area is in math. If you have any more questions or need further assistance, don’t hesitate to ask on WHAT.EDU.VN. Our team and community are here to provide free and accurate answers to all your questions.
Ready to take your math skills to the next level? Visit WHAT.EDU.VN today and unlock a world of free learning resources!
Do you find it challenging to find quick and free answers to your questions? Are you unsure where to turn for reliable information? At WHAT.EDU.VN, we understand these challenges and offer a platform where you can ask any question and receive prompt, accurate answers from knowledgeable individuals.
Don’t let your curiosity be stifled. Visit WHAT.EDU.VN today and start asking your questions. Our community is ready and eager to help you find the answers you seek.
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: WHAT.EDU.VN
Let what.edu.vn be your go-to resource for all your questions. Ask anything, learn everything!