What Is Associative Property? At WHAT.EDU.VN, we simplify complex math concepts! Discover how this fundamental property works with addition and multiplication to make calculations easier. Explore associative law, grouping numbers, and simplifying expressions.
1. What Is the Associative Property?
The associative property states that when adding or multiplying three or more numbers, the grouping of the numbers does not affect the final result. In simpler terms, you can change the parentheses without changing the answer. This concept is crucial for understanding basic arithmetic and algebraic manipulations. With WHAT.EDU.VN, mastering math is accessible and free, so ask your questions today.
This property applies to both addition and multiplication, but not to subtraction or division. Let’s break it down further:
- Addition: (a + b) + c = a + (b + c)
- Multiplication: (a × b) × c = a × (b × c)
The associative property is a cornerstone of mathematical operations, offering flexibility in how we approach calculations. If you are finding it hard to grasp the meaning of this, don’t hesitate to ask WHAT.EDU.VN.
2. Associative Property of Addition Explained
The associative property of addition means that how you group numbers when adding them together doesn’t change the sum. Whether you add the first two numbers first or the last two, the result will be the same.
Formula:
(x + y) + z = x + (y + z)
Example:
(2 + 3) + 4 = 2 + (3 + 4)
5 + 4 = 2 + 7
9 = 9
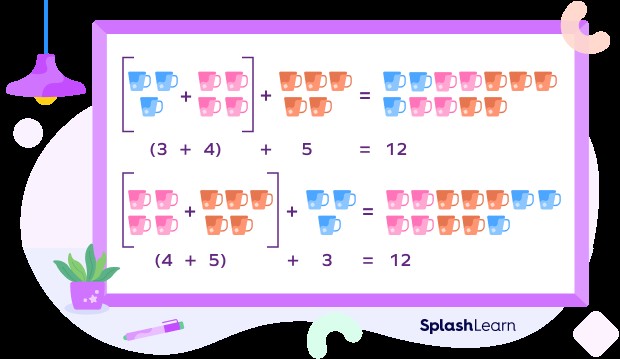Associative property of addition explained.
Here, regardless of whether you add 2 and 3 first or 3 and 4 first, the final sum is always 9. This principle simplifies complex addition problems, especially when dealing with multiple numbers. If you need more examples, visit WHAT.EDU.VN for personalized help.
3. Associative Property of Multiplication Explained
Similar to addition, the associative property of multiplication states that the grouping of numbers being multiplied does not affect the final product. You can multiply the first two numbers or the last two numbers first; the answer will remain the same.
Formula:
(p × q) × r = p × (q × r)
Example:
(2 × 3) × 4 = 2 × (3 × 4)
6 × 4 = 2 × 12
24 = 24
This demonstrates that whether you multiply 2 and 3 first or 3 and 4 first, the final product is always 24. This is particularly useful in simplifying expressions in algebra and other advanced mathematical fields. Do you want to master this concept? Go to WHAT.EDU.VN and ask away.
4. Commutative Property vs. Associative Property
It’s easy to confuse the associative and commutative properties, but there’s a key difference:
- Commutative Property: This property states that the order of numbers does not affect the result. For addition, a + b = b + a, and for multiplication, a × b = b × a.
- Associative Property: As we’ve discussed, this property states that the grouping of numbers does not affect the result.
The main difference lies in what changes: order (commutative) versus grouping (associative).
Example Illustrating the Difference:
- Commutative: 2 + 3 = 3 + 2 (Order changes)
- Associative: (2 + 3) + 4 = 2 + (3 + 4) (Grouping changes)
Understanding this distinction is essential for mastering basic mathematical principles. If you still find this confusing, WHAT.EDU.VN is here to provide clear, simple explanations.
5. Why Associative Property Doesn’t Apply to Subtraction
The associative property does not hold true for subtraction because changing the grouping of numbers alters the result.
Example:
10 – (5 – 2) ≠ (10 – 5) – 2
10 – 3 ≠ 5 – 2
7 ≠ 3
As the example shows, changing the grouping in a subtraction problem leads to different answers. For subtraction, the order and grouping are critical. If you need to understand why certain properties apply to some operations and not others, ask WHAT.EDU.VN.
6. Why Associative Property Doesn’t Apply to Division
Similarly, the associative property does not apply to division. The way numbers are grouped in a division problem affects the outcome.
Example:
(20 ÷ 4) ÷ 2 ≠ 20 ÷ (4 ÷ 2)
5 ÷ 2 ≠ 20 ÷ 2
- 5 ≠ 10
This difference in results proves that the associative property cannot be applied to division. Understanding these limitations helps in avoiding common mistakes in mathematical calculations. WHAT.EDU.VN is always ready to clarify these subtle but important mathematical concepts.
7. Real-World Applications of the Associative Property
The associative property isn’t just a theoretical concept; it has practical applications in everyday life.
-
Calculating Totals:
- Imagine you’re adding up the cost of items at a store: (5 + 3) + 2 = 5 + (3 + 2). Whether you add the first two items or the last two, the total cost remains the same.
-
Simplifying Measurements:
- When combining lengths, the associative property helps simplify the process. For example, (2 feet + 3 feet) + 1 foot = 2 feet + (3 feet + 1 foot).
-
Cooking and Baking:
- When scaling recipes, you might use the associative property to adjust ingredient quantities. For instance, (2 × 0.5) × 4 = 2 × (0.5 × 4) when doubling a recipe twice.
-
Time Management:
- Scheduling tasks can involve using the associative property. If you have tasks taking 10 minutes, 15 minutes, and 20 minutes, you can group them as (10 + 15) + 20 or 10 + (15 + 20) to plan your time effectively.
-
Financial Calculations:
- When calculating expenses, the associative property allows you to group different costs in a way that’s most convenient for you. (50 + 30) + 20 = 50 + (30 + 20).
These examples show how the associative property simplifies everyday calculations and problem-solving. If you’re curious about more practical applications, explore WHAT.EDU.VN for additional insights.
8. How to Teach Associative Property to Students
Teaching the associative property can be straightforward with the right approach:
-
Start with Concrete Examples:
- Use physical objects like blocks to demonstrate grouping. Show that (2 blocks + 3 blocks) + 4 blocks is the same as 2 blocks + (3 blocks + 4 blocks).
-
Use Visual Aids:
- Draw diagrams or use interactive tools to visually represent the property. This helps students see how the grouping changes without affecting the result.
-
Relate to Real-Life Scenarios:
- Explain how the associative property is used in everyday situations like calculating costs or measuring ingredients.
-
Practice with Various Problems:
- Provide plenty of practice problems involving both addition and multiplication. Start with simple numbers and gradually increase complexity.
-
Emphasize the Difference from Commutative Property:
- Clearly explain the difference between changing the order (commutative) and changing the grouping (associative).
-
Use Games and Activities:
- Incorporate games and activities that make learning fun and engaging. For example, a card game where students group numbers to reach a target sum.
-
Encourage Exploration:
- Allow students to explore the property on their own and discover its limitations with subtraction and division.
By using these methods, teachers can effectively convey the associative property to students, ensuring they grasp this fundamental concept. And remember, WHAT.EDU.VN is a great resource for students and educators alike.
9. Common Mistakes to Avoid When Using Associative Property
Even with a solid understanding, it’s easy to make mistakes when applying the associative property:
-
Applying to Subtraction or Division:
- Remember, the associative property only applies to addition and multiplication. Avoid using it with subtraction or division, as it will lead to incorrect results.
-
Changing the Order of Numbers:
- The associative property involves changing the grouping, not the order. Confusing it with the commutative property can lead to errors.
-
Incorrectly Grouping Numbers:
- Ensure that you are only changing the parentheses and not altering the fundamental operation or values within the equation.
-
Forgetting the Limitations:
- Be aware that the associative property does not hold true for all mathematical operations. Always double-check if it applies to the specific problem you are solving.
-
Overcomplicating Simple Problems:
- While the associative property can simplify complex calculations, it’s not always necessary for simple ones. Avoid overthinking straightforward problems.
-
Not Verifying Results:
- Always verify your results to ensure that changing the grouping did not inadvertently alter the answer.
By being mindful of these common pitfalls, you can avoid mistakes and use the associative property effectively. If you need help identifying or correcting errors, WHAT.EDU.VN is here to assist you.
10. Examples of Associative Property in Algebraic Expressions
The associative property is frequently used in algebra to simplify expressions and solve equations.
-
Simplifying Expressions:
- Consider the expression: (2x + 3y) + 5x. Using the associative property, you can regroup it as 2x + (3y + 5x), which simplifies to 7x + 3y.
-
Combining Like Terms:
- In the expression: (4a + 2b) + 6a, you can rearrange it as 4a + (2b + 6a), which simplifies to 10a + 2b.
-
Solving Equations:
- When solving equations, the associative property can help rearrange terms for easier manipulation. For example, if you have (3x + 5) + 2 = 10, you can rewrite it as 3x + (5 + 2) = 10, which simplifies to 3x + 7 = 10.
-
Working with Polynomials:
- When adding polynomials, the associative property allows you to group like terms. For instance, (2x² + 3x) + (4x² + 2x) can be rearranged as 2x² + (3x + 4x²) + 2x, simplifying to 6x² + 5x.
-
Factoring Expressions:
- The associative property can also be used in reverse to factor expressions. For example, 6x + 9y + 3 can be seen as (6x + 9y) + 3, allowing you to factor out a common factor if needed.
-
Complex Algebraic Manipulations:
- In more complex expressions, such as (2(x + 1) + 3) + 4(x + 1), you can use the associative property to group and simplify terms: 2(x + 1) + (3 + 4(x + 1)), making it easier to combine like terms and solve.
These examples demonstrate how the associative property is a valuable tool in algebraic problem-solving. If you need further clarification or examples, visit WHAT.EDU.VN for expert assistance.
11. Advanced Concepts Related to Associative Property
Beyond basic arithmetic and algebra, the associative property is relevant in more advanced mathematical concepts.
-
Abstract Algebra:
- In abstract algebra, associativity is a fundamental property that defines algebraic structures like groups, rings, and fields. These structures require operations that are associative.
-
Linear Algebra:
- In linear algebra, matrix multiplication is associative: (AB)C = A(BC), where A, B, and C are matrices. This property is crucial for many matrix operations and transformations.
-
Functional Analysis:
- In functional analysis, the composition of functions is associative: (f ◦ g) ◦ h = f ◦ (g ◦ h), where f, g, and h are functions. This property is used in defining and analyzing function spaces.
-
Computer Science:
- In computer science, the associative property is used in parallel computing and distributed systems. Associative operations can be performed in any order, allowing for efficient parallelization.
-
Logic and Set Theory:
- In logic, the conjunction (AND) and disjunction (OR) operations are associative. In set theory, the union and intersection operations are also associative.
-
Category Theory:
- In category theory, associativity is a basic axiom that defines the composition of morphisms. This abstract framework provides a general language for describing mathematical structures and their relationships.
These advanced concepts show that the associative property is not just a simple rule, but a fundamental principle that underlies many areas of mathematics and related fields. If you’re interested in exploring these topics further, WHAT.EDU.VN can provide you with the resources and guidance you need.
12. Associative Property in Different Number Systems
The associative property holds true in various number systems, not just the familiar real numbers.
-
Integers:
- The associative property applies to both addition and multiplication of integers. For example, (-2 + 3) + 4 = -2 + (3 + 4) and (-2 × 3) × 4 = -2 × (3 × 4).
-
Rational Numbers:
- Rational numbers, which can be expressed as fractions, also follow the associative property. For example, (1/2 + 1/3) + 1/4 = 1/2 + (1/3 + 1/4) and (1/2 × 1/3) × 1/4 = 1/2 × (1/3 × 1/4).
-
Complex Numbers:
- Complex numbers, which have a real and imaginary part, adhere to the associative property as well. For example, ((1 + i) + (2 – i)) + 3i = (1 + i) + ((2 – i) + 3i) and ((1 + i) × (2 – i)) × 3i = (1 + i) × ((2 – i) × 3i).
-
Real Numbers:
- As we’ve seen, real numbers, including both rational and irrational numbers, follow the associative property.
-
Matrices:
- Matrices also follow the associative property under matrix multiplication, where (AB)C = A(BC).
Understanding that the associative property applies across different number systems reinforces its fundamental nature in mathematics. If you have questions about number systems, consult the experts at WHAT.EDU.VN for clarification.
13. Tips for Memorizing the Associative Property
Memorizing mathematical properties can be challenging, but here are some tips to help you remember the associative property:
-
Use Mnemonics:
- Create a mnemonic to associate the word “associative” with “grouping.” For example, “Associative means you can Associate numbers in different groups.”
-
Relate to Real Life:
- Think of real-life examples where grouping doesn’t change the outcome, such as adding items to a shopping cart in different orders.
-
Visual Aids:
- Use visual aids like color-coded equations to highlight the grouping. For example, use parentheses in different colors to show how numbers are grouped.
-
Practice Regularly:
- Practice solving problems using the associative property regularly. The more you use it, the easier it will be to remember.
-
Teach Someone Else:
- Teaching the property to someone else can reinforce your understanding and memory of it.
-
Create Flashcards:
- Make flashcards with the definition and examples of the associative property. Review them regularly.
-
Use Online Resources:
- Utilize online resources like interactive quizzes and videos to make learning more engaging.
By using these tips, you can effectively memorize the associative property and apply it with confidence. And remember, WHAT.EDU.VN is always available to provide additional learning resources and support.
14. The History and Origin of the Associative Property
The associative property, like many fundamental mathematical principles, has a history rooted in the development of mathematical thought over centuries.
-
Ancient Civilizations:
- While ancient civilizations like the Egyptians and Babylonians used mathematical operations extensively, they did not explicitly formulate the associative property as a general principle. Their focus was primarily on practical calculations.
-
Greek Mathematics:
- The Greeks, particularly Euclid, laid the groundwork for formalized mathematics. However, the associative property was not a central focus of their work.
-
Development in Algebra:
- The associative property became more explicitly recognized with the development of algebra. As mathematicians began to generalize arithmetic operations, the properties of these operations became more important.
-
19th-Century Formalization:
- The formalization of the associative property occurred primarily in the 19th century with the development of abstract algebra. Mathematicians like George Boole and others formalized the properties of algebraic structures, including associativity.
-
Modern Mathematics:
- In modern mathematics, the associative property is a fundamental axiom that defines many algebraic structures, such as groups, rings, and fields. Its importance is recognized across various branches of mathematics.
Understanding the history and origin of the associative property provides context for its significance in the broader landscape of mathematics. If you’re curious about the history of mathematical concepts, WHAT.EDU.VN is a great place to explore and ask questions.
15. Examples of Associative Property in Computer Programming
The associative property has significant applications in computer programming, particularly in optimizing code and parallel processing.
-
Parallel Computing:
- Associative operations can be easily parallelized because the order of computation does not affect the result. For example, summing an array of numbers can be done in parallel by dividing the array into chunks and summing each chunk independently, then combining the results.
-
String Concatenation:
- In many programming languages, string concatenation is an associative operation. For example, (”Hello, ” + ”world”) + ”!” is the same as ”Hello, ” + (”world” + ”!”).
-
Database Operations:
- In database systems, certain operations like union and intersection are associative. This allows the database management system to optimize query execution by reordering operations.
-
Functional Programming:
- Functional programming relies heavily on associative operations because they allow for easier composition and transformation of functions.
-
MapReduce:
- The MapReduce programming model, popular in big data processing, uses associative operations in the reduce step to combine intermediate results efficiently.
-
Expression Evaluation:
- Compilers can use the associative property to reorder arithmetic operations for better performance or to take advantage of specific hardware features.
These examples illustrate how the associative property is not just a theoretical concept, but a practical tool in computer programming. If you want to learn more about its applications in coding, WHAT.EDU.VN can connect you with experts who can provide real-world insights.
16. How Associative Property Simplifies Complex Calculations
The associative property simplifies complex calculations by allowing you to regroup numbers in a way that makes the problem easier to solve.
-
Mental Math:
- When adding a series of numbers mentally, the associative property allows you to group numbers that are easy to add together. For example, in the sum 17 + 23 + 7, you can regroup it as (17 + 7) + 23, which simplifies to 24 + 23 = 47.
-
Large Numbers:
- When dealing with large numbers, the associative property can help break down the problem into smaller, more manageable steps. For instance, in the product (25 × 4) × 17, you can first multiply 25 and 4 to get 100, then multiply 100 by 17 to get 1700.
-
Fractions and Decimals:
- The associative property is also useful when working with fractions and decimals. For example, in the sum (0.75 + 0.25) + 0.5, you can first add 0.75 and 0.25 to get 1, then add 0.5 to get 1.5.
-
Algebraic Expressions:
- As discussed earlier, the associative property simplifies algebraic expressions by allowing you to combine like terms more easily.
-
Problem Solving:
- In complex problem-solving scenarios, the associative property can help you rearrange the problem to make it more intuitive and easier to understand.
-
Efficiency:
- By regrouping numbers, you can often find a more efficient way to solve a problem, saving time and reducing the likelihood of errors.
These examples show that the associative property is a valuable tool for simplifying calculations in various contexts. For more tips on simplifying calculations, consult the resources and experts at WHAT.EDU.VN.
17. Fun Activities to Practice Associative Property
Learning math doesn’t have to be boring. Here are some fun activities to help you practice the associative property:
-
Card Game:
- Create a deck of cards with numbers on them. Have players draw three cards and use the associative property to create different equations. Award points for correct equations.
-
Block Building:
- Use building blocks to represent numbers. Have students group the blocks in different ways to demonstrate the associative property.
-
Online Games:
- Find online games that focus on the associative property. These games often provide a fun and interactive way to practice the concept.
-
Worksheet Challenges:
- Create worksheets with a variety of problems that require the use of the associative property. Make it a competition to see who can solve the problems correctly the fastest.
-
Real-Life Scenarios:
- Create real-life scenarios where students can apply the associative property. For example, have them calculate the total cost of items in a store by grouping the items in different ways.
-
Story Problems:
- Write story problems that require the use of the associative property to solve. This helps students understand how the property applies in practical situations.
-
Group Activities:
- Divide students into groups and have them work together to solve problems using the associative property. This promotes teamwork and collaboration.
By incorporating these fun activities, you can make learning the associative property more engaging and enjoyable. For more creative ideas and resources, visit WHAT.EDU.VN.
18. How to Explain Associative Property to a Child
Explaining mathematical concepts to children requires simplicity and relatable examples. Here’s how to explain the associative property to a child:
-
Start with a Simple Definition:
- “The associative property means that when you add or multiply numbers, it doesn’t matter how you group them. You’ll still get the same answer.”
-
Use Toys or Objects:
- “Let’s say you have 2 toy cars, 3 toy trucks, and 4 toy airplanes. If you add the cars and trucks first (2 + 3) and then add the airplanes (+ 4), you get the same number as if you add the trucks and airplanes first (3 + 4) and then add the cars (+ 2).”
-
Relate to Real-Life Situations:
- “Imagine you are packing a lunchbox. You have 1 apple, 2 bananas, and 3 oranges. It doesn’t matter if you put the apple and bananas in the box first (1 + 2) and then add the oranges (+ 3), or if you put the bananas and oranges in first (2 + 3) and then add the apple (+ 1). You’ll still have the same number of fruits in your lunchbox.”
-
Use Visual Aids:
- Draw pictures or use color-coded equations to illustrate the property.
-
Keep It Fun:
- Use games and activities to make learning enjoyable.
-
Encourage Questions:
- Encourage the child to ask questions and explore the concept on their own.
-
Simple Examples:
- (2 + 3) + 4 = 5 + 4 = 9
- 2 + (3 + 4) = 2 + 7 = 9
- (2 × 3) × 4 = 6 × 4 = 24
- 2 × (3 × 4) = 2 × 12 = 24
By using these techniques, you can effectively explain the associative property to a child in a way that is easy to understand and remember. For more tips on teaching math to children, visit WHAT.EDU.VN.
19. FAQ: Common Questions About Associative Property
Here are some frequently asked questions about the associative property:
| Question | Answer |
|---|---|
| What is the associative property? | The associative property states that when adding or multiplying three or more numbers, the grouping of the numbers does not affect the final result. |
| Does the associative property apply to subtraction? | No, the associative property does not apply to subtraction. Changing the grouping of numbers in a subtraction problem alters the result. |
| Does the associative property apply to division? | No, the associative property does not apply to division. The way numbers are grouped in a division problem affects the outcome. |
| What is the difference between the associative and commutative properties? | The commutative property states that the order of numbers does not affect the result, while the associative property states that the grouping of numbers does not affect the result. |
| Can you give an example of the associative property in real life? | Imagine you’re adding up the cost of items at a store: (5 + 3) + 2 = 5 + (3 + 2). Whether you add the first two items or the last two, the total cost remains the same. |
| How can I remember the associative property? | Use mnemonics, relate it to real life, use visual aids, practice regularly, teach someone else, create flashcards, and use online resources. |
| In which number systems does the associative property hold true? | The associative property holds true in integers, rational numbers, complex numbers, and real numbers. |
| How is the associative property used in computer programming? | The associative property is used in parallel computing, string concatenation, database operations, functional programming, MapReduce, and expression evaluation. |
| Can the associative property simplify complex calculations? | Yes, the associative property simplifies complex calculations by allowing you to regroup numbers in a way that makes the problem easier to solve, especially in mental math, with large numbers, fractions, decimals, and algebraic expressions. |
| How can I explain the associative property to a child? | Start with a simple definition, use toys or objects, relate to real-life situations, use visual aids, keep it fun, encourage questions, and provide simple examples. |
For more answers to your questions and expert guidance, visit WHAT.EDU.VN.
20. Test Your Knowledge: Associative Property Quiz
Test your understanding of the associative property with the following quiz:
-
Which of the following equations demonstrates the associative property of addition?
- a) 2 + 3 = 3 + 2
- b) (2 + 3) + 4 = 2 + (3 + 4)
- c) 2 × 3 = 3 × 2
- d) (2 × 3) × 4 = 2 × (3 × 4)
-
Which of the following operations does the associative property NOT apply to?
- a) Addition
- b) Multiplication
- c) Subtraction
- d) None of the above
-
Simplify the following expression using the associative property: (15 + 5) + 10
- a) 15 + (5 + 10) = 30
- b) 20 + 10 = 30
- c) Both a and b
- d) Neither a nor b
-
Which of the following is an example of the associative property in real life?
- a) Arranging books on a shelf in different orders
- b) Calculating the total cost of items in a store by grouping them differently
- c) Changing the order of ingredients in a recipe
- d) None of the above
-
Which number system does the associative property hold true in?
- a) Integers
- b) Rational Numbers
- c) Complex Numbers
- d) All of the above
Answers:
- b
- c
- c
- b
- d
How did you do? If you need to brush up on your knowledge, visit WHAT.EDU.VN for more resources and expert assistance.
At WHAT.EDU.VN, we’re dedicated to providing accessible and comprehensive explanations of mathematical concepts. If you have any questions or need further clarification, don’t hesitate to reach out. We’re here to help you succeed!
Address: 888 Question City Plaza, Seattle, WA 98101, United States
Whatsapp: +1 (206) 555-7890
Website: WHAT.EDU.VN
Are you struggling to understand math concepts? Do you need quick and reliable answers to your questions? WHAT.EDU.VN offers a free platform where you can ask any question and receive expert answers promptly. Stop struggling and start learning today with what.edu.vn. Ask your question now and experience the ease of learning with our free service.
