In mathematics, especially when exploring shapes, understanding the circumference is fundamental. Simply put, the circumference is the distance around any curved shape. Think of it as the outline or boundary that encloses the shape. For circles, the circumference is often referred to as the perimeter of a circle, and it tells us the length of the circle’s edge.
When we talk about circles, two key measurements are crucial: the circumference and area. This article focuses on the circumference of a circle, often phrased as “What Is Circumference,” diving into its definition, formulas, and various methods to calculate it, complete with examples to guide you.
Defining Circle Circumference
Circumference of a circle, or perimeter of a circle, is the measurement of the distance around the circle’s edge. In contrast, the area of a circle measures the space enclosed within the circle. Imagine unrolling a circle into a straight line; the length of that line would be its circumference. Circumference is measured in linear units like centimeters (cm) or meters (m).
Calculating the circumference of a circle relies on knowing its radius or diameter. These measurements are essential for applying the circumference formulas.
Circumference Formula: Unveiling the Magic of Pi
The formula to calculate the circumference (or perimeter) of a circle is:
Circumference (C) = 2πR
Where:
- R represents the radius of the circle (the distance from the center to any point on the circle).
- π (Pi) is a mathematical constant, approximately 3.14159, often rounded to 3.14 for simplicity.
Pi (π) is a fascinating number. It represents the ratio of any circle’s circumference to its diameter. This relationship gives us another key formula:
C = πD
Where:
- C is the circumference of the circle.
- D is the diameter of the circle (the distance across the circle through the center, which is twice the radius).
Example: Let’s say a circle has a radius of 4 cm. To find its circumference:
Circumference = 2πr
= 2 x 3.14 x 4
= 25.12 cm
Therefore, the circumference of the circle is 25.12 cm.
Exploring Area of a Circle
While our focus is circumference, it’s helpful to briefly touch upon the area of a circle. The area is the space enclosed within the circle’s boundary. The formula for the area of a circle is:
Area (A) = πr²
Where ‘r’ is the radius. This formula applies to all circles, regardless of size.
Circumference of a Semicircle
A semicircle is exactly half of a circle. To find the perimeter of a semicircle, we need to consider both the curved part (half the circumference of the full circle) and the straight diameter line that closes it off.
Perimeter of Semicircle = πr + 2r
This formula adds half the circumference (πr) to the diameter (2r).
Area of a Semicircle
Similarly, the area of a semicircle is half the area of a full circle with the same radius.
Area of Semicircle = πr²/2
Formulas for Circumference: A Quick Guide
Let’s summarize the different ways to calculate circumference based on what information you have:
Formula 1: Using Radius
Circumference = 2πr
Formula 2: Using Diameter
Circumference = πd
Formula 3: Using Area (Less Common but Possible)
Circumference = √(4πA)
Where A is the area of the circle. This formula is derived by first finding the radius from the area formula and then substituting it into the circumference formula.
Summary Table
| Measurement | Formula |
|---|---|
| Circumference of Circle | 2πr or πd |
| Area of Circle | πr² |
| Perimeter of Semicircle | πr + 2r |
| Area of Semicircle | πr²/2 |
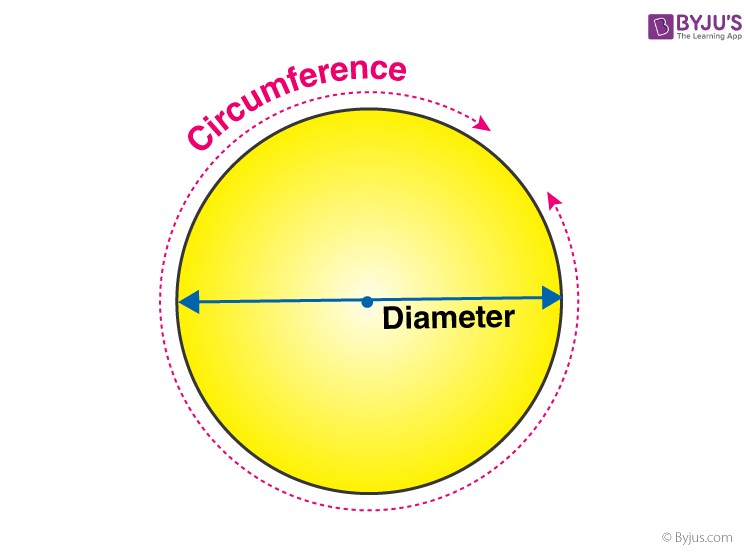
Understanding the Radius
The radius of a circle is the distance from the exact center of the circle to any point on its outer edge. It is a fundamental measurement for all circle calculations. The diameter, as mentioned, is simply twice the radius.
What Does “Circumference” Really Mean?
The term “circumference” originates from Latin, meaning “carrying around.” In geometry, it precisely describes the linear distance around a curved shape, especially circles. It’s a one-dimensional measurement of a two-dimensional shape’s boundary. Calculating circumference is fundamentally the same concept as finding the perimeter of polygons – measuring the outer boundary. Therefore, when you’re asked “what is circumference,” remember it’s essentially the perimeter for circles and similar curved shapes.
A circle is unique because every point on its edge is equidistant from the central point. Let’s visualize a circle with center point ‘A’:
The image above visually represents the circumference as the distance around the circle and the diameter as the line across the circle passing through the center.
The constant π is the ratio of a circle’s circumference to its diameter. No matter the size of the circle, dividing its circumference by its diameter will always yield a value very close to π (approximately 3.14159…). This relationship is expressed as:
C/d = π
Which rearranges to the more common formula:
C = π × d
This formula is particularly useful when you know the diameter and need to calculate the circumference.
Circumference to Diameter Ratio
As we’ve emphasized, the ratio of the circumference to the diameter of any circle is always Pi (π). This constant ratio is the very definition of π.
C = 2πr (and since d = 2r)
C = πd
Dividing both sides by the diameter (d) gives us:
C/d = π
This fundamental relationship highlights the significance of π in understanding circles.
Methods to Find Circumference
Method 1: Direct Measurement (Less Precise)
While not practical for precise calculations, you can conceptually measure circumference using a thread. Carefully place a thread along the circle’s edge, mark where it completes one full circle, and then measure the thread’s length with a ruler. This gives an approximate circumference.
Method 2: Calculation (Accurate)
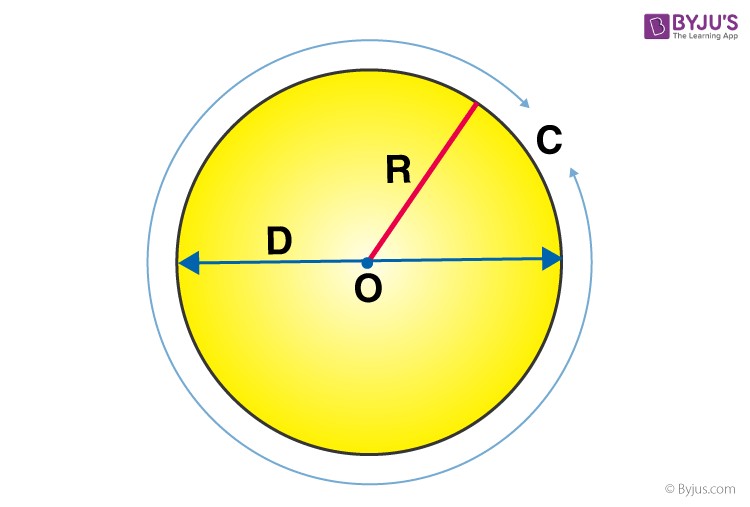
The most accurate way to find circumference is through calculation using formulas. This requires knowing either the radius or diameter of the circle. The radius is the distance from the center to any point on the circle’s edge.
The image illustrates a circle with center ‘O’ and radius ‘R’, visually reinforcing the concept of radius in circumference calculation.
Solved Examples: Putting Formulas into Practice
Let’s work through some examples to solidify your understanding of circumference calculation.
Example 1:
What is the circumference of a circle with a diameter of 4 cm?
Solution:
Given: Diameter (d) = 4 cm
Using the formula: C = πd
C = 3.14 x 4
C = 12.56 cm
Example 2:
Find the radius of a circle if its circumference (C) is 50 cm.
Solution:
Given: Circumference (C) = 50 cm
Using the formula: C = 2πr
50 = 2πr
r = 50 / (2π)
r = 25 / π cm (approximately 7.96 cm using π ≈ 3.14)
Example 3:
Calculate the perimeter of a circle with a radius of 3 cm.
Solution:
Given: Radius (r) = 3 cm
Using the formula: C = 2πr
C = 2 x (22/7) x 3 (using π ≈ 22/7 for this example)
C ≈ 18.857 cm
Example 4:
Find the perimeter of a circle in terms of π, whose diameter is 10m.
Solution:
Given: Diameter (d) = 10 m
Using the formula: C = πd
C = π x 10
C = 10π m
Example 5:
Find both the perimeter (circumference) and area of a circle with a radius of 5 cm. (Use π = 3.14)
Solution:
Given: Radius (r) = 5 cm, π = 3.14
Area (A) = πr² = 3.14 x (5)² = 3.14 x 25 = 78.5 cm²
Circumference (C) = 2πr = 2 x 3.14 x 5 = 31.4 cm
Therefore, the area is 78.5 cm² and the circumference is 31.4 cm.
Practice Questions
Test your understanding with these practice problems:
- Calculate the perimeter of a circle with a diameter of 8 cm.
- What is the diameter of a circle if its circumference is 10 cm?
- If the circumference is 12 cm, what is its radius?
- What is the circumference of a 16-inch circle?
- What is the circumference of a 6 mm circle?
Learn More About Circles (Video)
[Insert Video Placeholder or Link Here – Original article has image link]
To deepen your understanding of circles and related concepts, explore further resources and interactive tools.
Frequently Asked Questions (FAQs) About Circumference
Q1: What is the Circumference of a Circle?
A: The circumference is the distance around the circle, the length of its boundary. Imagine unrolling the circle into a straight line; that line’s length is the circumference.
Q2: How do you Calculate Circumference?
A: You can calculate circumference using two main formulas: C = πd (using diameter) or C = 2πr (using radius). Multiply the diameter by π or twice the radius by π (where π ≈ 3.14).
Q3: How to Find Diameter from Circumference?
A: Rearrange the formula C = πd to solve for diameter: Diameter = Circumference / π.
Q4: What is the Circumference of a Circle with a 24-inch Radius?
A: C = 2πr = 2 x 3.14 x 24 = 150.72 inches.
Q5: Steps to Find Circumference if Area is Given?
A: 1. Find the radius using the area formula (A = πr²). Solve for r: r = √(A/π). 2. Use the radius in the circumference formula (C = 2πr) to calculate the circumference.
Q6: Formula for Perimeter (Circumference) when Area is Known?
A: C = 2√(πA)
Q7: Circumference in terms of π if Radius is 3 cm?
A: C = 2πr = 2π(3) = 6π cm.
Q8: Circumference in terms of π if Diameter is 7 cm?
A: C = πd = π(7) = 7π cm.
By understanding these formulas and concepts, you can confidently calculate the circumference of any circle and grasp the fundamental properties of this essential geometric shape.
