In statistics, a confidence interval estimates the range within which a population parameter is likely to fall for a given proportion of times. Analysts frequently use confidence intervals representing 95% or 99% of expected observations. For instance, if a statistical model estimates a value of 10.00 with a 95% confidence interval of 9.50 to 10.50, it suggests that we are 95% confident that the true value lies within this range.
Statisticians and data analysts use confidence intervals to assess the statistical significance of estimations, inferences, and predictions. If a confidence interval includes zero (or another null hypothesis value), one cannot definitively conclude that a result from testing or experimentation is attributable to a specific cause rather than chance.
Key Takeaways
- A confidence interval indicates the probability that a population parameter will fall between a pair of values around the mean.
- Confidence intervals quantify the uncertainty or certainty in a sampling method.
- They are also applied in hypothesis testing and regression analysis.
- Statisticians often use p-values alongside confidence intervals to assess statistical significance.
- They are commonly constructed using confidence levels of 95% or 99%.
Understanding Confidence Intervals
Confidence intervals measure the degree of uncertainty or certainty in a sampling method. They can represent various probability limits, with 95% or 99% confidence levels being the most common. These intervals are determined through statistical methods like the t-test.
Statisticians use confidence intervals to gauge the uncertainty in an estimate of a population parameter derived from a sample. For example, a researcher might take multiple random samples from the same population and calculate a confidence interval for each to observe how well they represent the population variable’s true value. The resulting datasets will vary; some intervals will include the true population parameter, while others will not.
:max_bytes(150000):strip_icc():format(webp)/dotdash_Final_Understanding_Confidence_Intervals_v1-01-90c5349744c1469c99b8384af54945d1.png “Bell curve illustration showing the distribution of data within confidence intervals.”)
A confidence interval is a range of values—bounded above and below a statistic’s mean—that is likely to contain an unknown population parameter. The confidence level indicates the probability (or certainty) that the confidence interval will contain the true population parameter when drawing a random sample repeatedly.
In simpler terms, a 99% confidence level suggests “we are 99% certain that most of these samples (confidence intervals) contain the true population parameter.”
A common misconception is that confidence intervals represent the percentage of data within a sample falling between the upper and lower bounds. For example, the aforementioned 99% confidence interval of 70 to 78 inches doesn’t mean that 99% of the data in a random sample falls within this range.
While incorrect, there is a separate statistical analysis method for determining such a figure, involving identifying the sample’s mean and standard deviation and plotting these values on a bell curve.
Important Note
Confidence intervals and confidence levels are related but distinct concepts. The confidence level determines the method’s ability to produce confidence intervals that include the true parameter.
Calculating Confidence Intervals
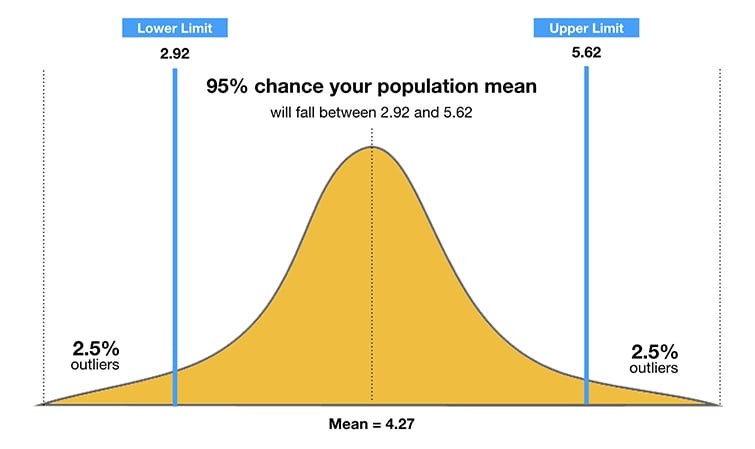
Consider a group of researchers studying the heights of high school basketball players. They take a random sample from the population and find a mean height of 74 inches.
This 74-inch mean is a point estimate of the population mean. However, a point estimate alone is insufficient because it doesn’t show the uncertainty associated with the estimate; one can’t discern how far this 74-inch sample mean is from the population mean. What’s missing is the level of uncertainty in this single sample.
Confidence intervals offer more information than point estimates. By calculating a 95% confidence interval using the sample’s mean and standard deviation, and assuming a normal distribution (represented by the bell curve), the researchers can determine an upper and lower bound that contains the true mean 95% of the time.
Suppose the interval is between 72 and 76 inches. If the researchers take 100 random samples from the population of high school basketball players, the mean should fall between 72 and 76 inches in 95 of those samples.
If the researchers desire even greater confidence, they can expand the interval to a 99% confidence level. This invariably creates a broader range to accommodate more sample means. If the 99% confidence interval is established as being between 70 and 78 inches, they can expect 99 out of 100 samples evaluated to contain a mean value within this range.
A 90% confidence level, on the other hand, implies that 90% of the interval estimates are expected to include the population parameter, and so forth.
What Does a Confidence Interval Reveal?
A confidence interval is a range of values—bounded above and below the statistic’s mean—that likely contains an unknown population parameter. The confidence level represents the probability or certainty that the confidence interval will contain the true population parameter when you draw a random sample many times.
 Confidence interval example
Confidence interval example
Why Are Confidence Intervals Used?
Statisticians use confidence intervals to measure uncertainty in a sample variable. For example, a researcher selects different samples randomly from the same population and computes a confidence interval for each sample to see how it may represent the true value of the population variable. The resulting datasets are all different, with some intervals including the true population parameter and others not.
What Is a Common Misconception About Confidence Intervals?
The biggest misconception regarding confidence intervals is interpreting them as the percentage of data from a given sample that falls between the upper and lower bounds. It’s incorrect to assume a 99% confidence interval means 99% of the data in a random sample falls between these bounds. The correct interpretation is that one can be 99% certain that the range contains the population mean.
What Is a T-Test?
Confidence intervals are often calculated using statistical methods like the t-test. A t-test is a type of inferential statistic used to determine if there is a significant difference between the means of two groups, which may be related to certain features. Calculating a t-test requires three key data values: the difference between the mean values from each dataset (the mean difference), the standard deviation of each group, and the number of data values in each group.
How Do You Interpret P-Values and Confidence Intervals?
A p-value is a statistical measurement used to validate a hypothesis against observed data. It measures the probability of obtaining the observed results, assuming the null hypothesis is true. Generally, a p-value less than 0.05 is considered statistically significant, leading to the rejection of the null hypothesis. This often corresponds to the probability that the null hypothesis value (often zero) is contained within a 95% confidence interval.
The Bottom Line
Confidence intervals help analysts understand the likelihood that results from statistical analyses are genuine rather than due to chance. When making inferences or predictions based on a sample of data, there’s inherent uncertainty about whether the analysis results accurately reflect the real-world population being studied. The confidence interval illustrates the likely range within which the true value should fall.